Математика 2к (2). При решении системы n линейных уравнений с n переменными можно воспользоваться формулами Крамера, если
 Скачать 40.33 Kb. Скачать 40.33 Kb.
|
|
1. При решении системы n линейных уравнений с n переменными можно воспользоваться формулами Крамера, если … 1. один из столбцов матрицы коэффициентов является линейной комбинацией остальных 2. столбцы матрицы коэффициентов линейно независимы 3. определитель матрицы коэффициентов не равен нулю 4. строки матрицы коэффициентов линейно зависимы Ответ: 3. определитель матрицы коэффициентов не равен нулю 2 Бинарными на множестве натуральных чисел являются операции … 1. сложение и вычитание 2. сложение и деление 3. умножение и вычитание 4. сложение и умножение Ответ: 4. сложение и умножение 3 Формула вычисления определителя третьего порядка 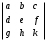 содержит произведения … содержит произведения …1. cdk 2. bfg 3. adf 4. cfh Ответ: 2. bfg 4 Формула вычисления определителя третьего порядка 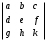 содержит произведения со знаком «+» содержит произведения со знаком «+»1. cdk 2. bfg 3. aek 4. cfh Ответ: 3. aek 5 Формула вычисления определителя третьего порядка 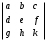 содержит произведения со знаком «-» содержит произведения со знаком «-»1. cdk 2. bfg 3. adf 4. dbk Ответ: 4. dbk 6 Даны матрицы 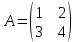 и В = и В = 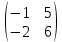 . Элемент 1-й строки и 2-ого столбца суммы А+ 2В равен … . Элемент 1-й строки и 2-ого столбца суммы А+ 2В равен …1. 12 2. 10 3. 36 4. 16 Ответ: 1. 12 7 Даны матрицы 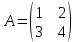 и В = и В = 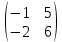 . Элемент 1-й строки и 1-ого столбца разности А-В равен … . Элемент 1-й строки и 1-ого столбца разности А-В равен …1. 2 2. 1 3. 0 4. 3 Ответ: 1. 2 8 Квадратная матрица называется вырожденной, если её определитель равен … 1. 2 2. 1 3. 0 4. 3 Ответ: 3. 0 9 Решая систему 4-х линейных уравнений с 4-мя неизвестными методом Гаусса получили матрицу: 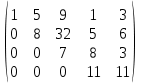 , значит данная система … , значит данная система …1. имеет единственное решение 2. имеет бесконечное множество решений 3. не имеет решений 4. имеет два ненулевых решения Ответ: 1. имеет единственное решение 10 Выберите верное соответствие между типом системы m линейных уравнений c n переменными и количеством её решений: 1. несовместная система - нет решений 2. совместная определённая система - два решения 3. совместная неопределённая система - n решений Ответ: 1. несовместная система - нет решений 2. совместная определённая система - два решения 3. совместная неопределённая система – n решений 11 Вычислите (cosx)’=: 1. -sinx 2. -cosx 3. sinx Ответ: 1. -sinx 12 Вычислите (kx+b)’=: 1. x+b 2. k 3. k+b Ответ: 2. k 13 Вычислите (5x)’=: 1. 5 2. 5x 4 3. 0 Ответ: 2. 5x4 14 Установите соответствие между функцией и ее производной: sin (x/2): 1. 1/2 cos (х/2) 2. -sin (x/2) 3. -4 cos 2x Ответ: 1. 1/2 cos (х/2) 15 Вычислите (sinx)’=: 1. -cosx 2. sinx 3. cosx Ответ: 3. cosx 16 Установите соответствие между функцией и ее производной: cos 2x: 1. -4 cos 2x 2. -2 sin 2х 3. -sin (x/2) Ответ: 2. -2 sin 2х 17 Установите соответствие между функцией и ее производной: -2 sin 2x: 1. -4 cos 2x 2. 1/2 cos (х/2) 3. -sin (x/2) Ответ: 1. -4 cos 2x 18 Вычислите (10x)’=: 1. x 2. 1 3. 10 Ответ: 3. 10 19 Установите соответствие между функцией и ее производной: 2 cos (x/2): 1. 1/2 cos (х/2) 2. -sin (x/2) 3. -4 cos 2x Ответ: 1. 1/2 cos (х/2) 20 Вычислите (lnx)’=: 1. 1/x 2. 1 3. 0 Ответ: 1. 1/x 21 Укажите точку максимума функции f(x), если f´ (x)=(x+6)(x-4): 1. 6 2. 5 3. -6 Ответ: 3. -6 22 Укажите производную функции y=6x-11: 1. 11 2. 6 3. -5 Ответ: 2. 6 23 Функцией называется: 1. множество всех значений, которые может принимать функция 2. множество всех точек (x; f(x)) на координатной плоскости, где x принадлежит D 3. закон, по которому каждому значению x из множества D ставится в соответствие одно определенное число y Ответ: 3. закон, по которому каждому значению x из множества D ставится в соответствие одно определенное число y 24 В чём состоит физический смысл производной: 1. это расстояние 2. это мгновенная скорость 3. это время Ответ: 2. это мгновенная скорость 25 Чему равен угловой коэффициент прямой y=-2x+3: 1. -2 2. 3 3. 2 Ответ: 1. -2 26 Функция f называется убывающей на некотором промежутке: 1. если x2 > x1, то f(x2)=f(x1) 2. если x2 > x1, то f(x2) > f(x1) 3. если x2 > x1, то f(x2) < f(x1) Ответ: 3. если x2 > x1, то f(x2) < f(x1) 27 Как называется точка, в которой f ‘(x) меняет знак с ” + ” на ” – “: 1. точка минимума 2. экстремум 3. точка максимума Ответ: 2. экстремум 28 Функция f называется нечетной, если для любого х из ее области определения значение -х также принадлежит области определения и верно равенство: 1. f(x)=-f(x) 2. f(-x)=f(x) 3. f(-x)=-f(x) Ответ: 3. f(-x)=-f(x) 29 Функция f называется возрастающей на некотором промежутке: 1. если x2 > x1, то f(x2) > f(x1) 2. если x2 > x1, то f(x2)=f(x1) 3. если x2 > x1, то f(x2) < f(x1) Ответ: 1. если x2 > x1, то f(x2) > f(x1) 30 Понятие дифференциального исчисления, характеризующее скорость изменения функции в данной точке: 1. четная функция 2. производная функции 3. нечетная функция Ответ: 2. производная функции 31 Неопределенный интеграл от функции - это… 1. первообразная функции 2. площадь криволинейной трапеции, ограниченной графиком функции, осью абсцисс и еще двумя прямыми 3. совокупность всех первообразных функции Ответ: 3. совокупность всех первообразных функции 32 Если прямая перпендикулярна к плоскости, то она перпендикулярна лежащим в этой плоскости двум сторонам треугольника, так ли это: 1. да 2. нет 3. зависит от условия задачи Ответ: 1. да 33 К методам интегрирования относятся: 1. интегрирование по частям 2. метод Гаусса 3. дифференцирование Ответ: 1. интегрирование по частям 35 Определенный интеграл – это (отметьте верные утверждения)… 1. площадь криволинейной трапеции, ограниченной графиком этой функции 2. разложение неопределенного интеграла на множители 3. для неположительной функции площадь криволинейной трапеции, ограниченной графиком этой функции, прямыми х = а, х = b и осью абсцисс, взятая со знаком минус Ответ: 3. для неположительной функции площадь криволинейной трапеции, ограниченной графиком этой функции, прямыми х = а, х = b и осью абсцисс, взятая со знаком минус 35 Для любой непрерывной функции всегда существует 1. бесконечное множество первообразных 2. только одна первообразная 3. две различных первообразных, которые отличаются знаком, стоящим перед первым слагаемым 4. другой ответ Ответ: 1. бесконечное множество первообразных 36 Укажите первообразную функции  1.  2.  3.  4.  Ответ: 3.  37 Найти первообразную функции f(x) = cosx+cos(-x) 1. C 2. -2cosx+C 3. 2sinx +C 4. -2sinx +C Ответ: -2sinx +C 38 Найти первообразную функции у=8x3 1. 4х3 2. 2х4 3. 2х3 4. 4х2 Ответ: 2. 2х4 39 Найти первообразную функции у=x, график которой проходит через точку Р(3;5) 1) x2 +4 2) 2x2 +4 3) 4x2 -4 4) x2 -4 Ответ: 2) 2x2 +4 40 Вычислить площадь фигуры, ограниченной линиями у=6х2 и у=0; х=1; х=2 1. 5 2. 14 3. 11 4. 2 Ответ: 2. 14 |
