актуальность 1. Применение современных технологий на уроках математики
 Скачать 2.8 Mb.
|
|
Кейс №1. Расстояние от точки до прямой AF (ABC). Найдите расстояние от F до CB. 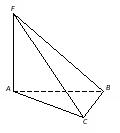 ΔАВС– равнобедренный ΔАВС – прямоугольный, С = 900 ΔАВС – тупоугольный, С > 900 ВF (ABC). Найдите расстояние от F до АС. 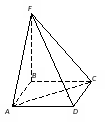 ABCD – квадрат ABCD – ромб ABCD – прямоугольник BS (ABC). ABCDEF – правильный шестиугольник. Найдите расстояние 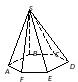 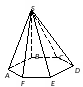 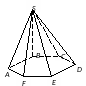 Задачи 1.1.1. В основании пирамиды FABC лежит равнобедренный треугольник АВС, АВ=АС=10, ВС=12. Ребро AF перпендикулярно плоскости основания и равно 6. Найдите расстояние от вершины F до ребра ВС. О т в е т: 10. 1.1.2. В основании пирамиды FABC лежит прямоугольный треугольник АВС, С = 900, ВС=12. Ребро AF перпендикулярно плоскости основания. Расстояние от вершины F до ребра ВС равно 5. Найдите расстояние от вершины F до вершины В. О т в е т: 13. 1.1.3. В основании пирамиды FABC лежит равнобедренный тупоугольный треугольник АВС, С = 1200, АС=СВ=  . Ребро AF перпендикулярно плоскости основания. Расстояние от вершины F до ребра ВС равно 5. Найдите расстояние от вершины F до плоскости АВС.О т в е т: 4. 1.2.1. В основании пирамиды FABCD лежит квадрат ABCD со стороной равной 4. Ребро BF перпендикулярно плоскости основания и равно 1. Найдите расстояние от точки F до диагонали АС. О т в е т: 3. 1.2.2. Основанием пирамиды FABCD является ромб ABCD с углом А равным 600 и радиусом вписанной окружности  . Ребро BF перпендикулярно плоскости основания. Найдите длину ребра BF, если расстояние от точки F до диагонали ромба АС рано  .О т в е т: 4. 1.2.3. В основании пирамиды FABCD лежит прямоугольник ABCD со сторонами 3 и 4. Ребро BF перпендикулярно плоскости основания. Найдите высоту пирамиды, если расстояние от точки F до диагонали прямоугольника АС рано 2,5. О т в е т: 0,7. 1.3.1. Основанием пирамиды SABCDEF является правильный шестиугольник ABCDEF со стороной . Ребро BS перпендикулярно плоскости основания. Найдите расстояние от вершины S до стороны АВ, если расстояние от вершины S до ребра EF равно 5.О т в е т: 4. 1.3.2. В основании пирамиды SABCDEF лежит правильный шестиугольник ABCDEF со стороной . Ребро BS перпендикулярно плоскости основания и равно 2. Найдите расстояние от вершины S до стороны AF.О т в е т: 2,5. 1.3.3. В основании пирамиды SABCDEF лежит правильный шестиугольник ABCDEF, большая диагональ которого равна  . Ребро BS перпендикулярно плоскости основания и равно 5. Найдите расстояние от вершины S до стороны EF.О т в е т: 13. Кейс № 2 II. Угол между прямой и плоскостью АА1 (АВС). Найдите угол между СB1 и (АА1С1). 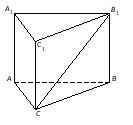 ΔАВС– равносторонний ΔАВС – прямоугольный, С = 900 ΔАВС – тупоугольный, С > 900 2) АА1 (АВС). ABCDFK – правильный шестиугольник. Найдите угол между 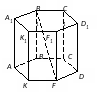 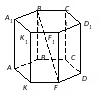 3)BD (АВС). Найдите угол между CD и (ABD). ΔАВС – прямоугольный, А = 900 ΔАВС – прямоугольный, С = 900 АА1 (АВС). Найдите углы между A B C D к в а д р а т 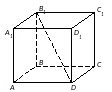 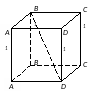 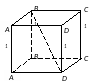 A B C D р о м б 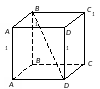 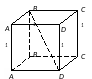 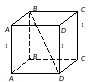 BF (АВС). Найдите угол между A B C D к в а д р а т 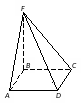 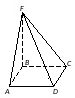 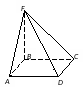 A B C D р о м б 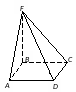 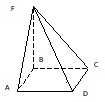 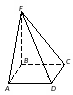  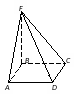|