Примеры решений задач ТВиМС. Примеры решений типовых задач
 Скачать 478.93 Kb. Скачать 478.93 Kb.
|
|
Пример 7.9 В вычислительный центр коллективного пользования с тремя ЭВМ поступают заказы от предприятий на вычислительные работы. Если работают все три ЭВМ, то вновь поступающий заказ не принимается, и предприятие вынуждено обратиться в другой вычислительный центр. Среднее время работы с одним заказом составляет 3 ч. Интенсивность потока заявок 0,25 1/ч. Найти предельные вероятности состояний и показатели эффективности работы вычислительного центра. Решение По условию п=3, λ=0,25 (1/ч), to6=3 (ч). Интенсивность потока обслуживаний μ=1/ to6=1/3=0,33. Интенсивность нагрузки ЭВМ по формуле (7.28) р=0,25/0,33=0,75. Найдем предельные вероятности состояний: по формуле (7.29): p0=(1+0,75+0,752/2!+0,753/3!)-1=0,476; по формуле (7.30): p1 = 0,75*0,476 = 0,357; p2 = (0,752/2!)*0,476 = 0,134; p3 = (0,753/3!)*0,476 = 0,033, т.е. в стационарном режиме работы вычислительного центра в среднем 47,6% времени нет ни одной заявки, 35,7% – имеется одна заявка (занята одна ЭВМ), 13,4% – две заявки (две ЭВМ), 3,3% времени – три заявки (заняты три ЭВМ). Вероятность отказа (когда заняты все три ЭВМ), таким образом, Р0ТК= р3=0,033. Согласно формуле (7.32) относительная пропускная способность центра Q= 1 – 0,033 = 0,967, т.е. в среднем из каждых 100 заявок вычислительный центр обслуживает 96,7 заявок. По формуле (7.33) абсолютная пропускная способность центра А= 0,250,967 = 0,242, т.е. в один час в среднем обслуживается 0,242 заявки. Согласно формуле (7.34) среднее число занятых ЭВМ к == 0,242/0,33 = 0,725, т.е. каждая из трех ЭВМ будет занята обслуживанием заявок в среднем лишь на 72,5/3 = 24,2%. При оценке эффективности работы вычислительного центра необходимо сопоставить доходы от выполнения заявок с потерями от простоя дорогостоящих ЭВМ (с одной стороны, здесь высокая пропускная способность СМО, а с другой – значительный простой каналов обслуживания) и выбрать компромиссное решение. Задания 7.1. Случайный процесс определяется формулой X(t)= Хе(- t) ( t> 0), где X– случайная величина, распределенная по нормальному закону с параметрами аи а2. Найти математическое ожидание, дисперсию, корреляционную и нормированную корреляционную функции случайного процесса. 7.2. Построить граф состояний следующего случайного процесса: система состоит из двух автоматов по продаже газированной воды, каждый из которых в случайный момент времени может быть либо занятым, либо свободным. 7.3. Построить граф состояний системы S,представляющей собой электрическую лампочку, которая в случайный момент времени может быть либо включена, либо выключена, либо выведена из строя. 7.4. Среднее число заказов на такси, поступающих на диспетчерский пункт в одну минуту, равно 3. Найти вероятность того, что за две минуты поступит: а) 4 вызова; б) хотя бы один; в) ни одного вызова. (Поток заявок простейший.) 7.5. Найти предельные вероятности для систем S,граф которых изображен на рис. 7.11 и 7.12. 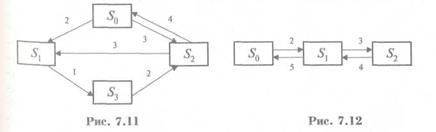 7.6. Рассматривается круглосуточная работа пункта проведения профилактического осмотра автомашин с одним каналом (одной группой проведения осмотра). На осмотр и выявление дефектов каждой машины затрачивается в среднем 0,5 ч. На осмотр поступает в среднем 36 машин в сутки. Потоки заявок и обслуживаний – простейшие. Если машина, прибывшая в пункт осмотра, не застает ни одного канала свободным, она покидает пункт осмотра необслуженной. Определить предельные вероятности состояний и характеристики обслуживания профилактического пункта осмотра. 7.7. Решить задачу 7.15 для случая п= 4 канала (групп проведения осмотра). Найти минимальное число каналов, при котором относительная пропускная способность пункта осмотра будет не менее 0,9. 7.8. Одноканальная СМО с отказами представляет собой одну телефонную линию, на вход которой поступает простейший поток вызовов с интенсивностью 0,4 вызовов/мин. Средняя продолжительность разговора 3 мин.; время разговора имеет показательное распределение. Найти предельные вероятности состояний и характеристики обслуживания СМО. Сравнить пропускную способность СМО с номинальной, которая была бы, если разговор длился в точности 3 мин., а заявки шли одна за другой регулярно, без перерывов. 7.9. Имеется двухканальная простейшая СМО с отказами. На ее вход поступает поток заявок с интенсивностью 4 заявки/ч. Среднее время обслуживания одной заявки 0,8 ч. Каждая обслуженная заявка приносит доход 4 ден. ед. Содержание каждого канала обходится 2 ден. ед./ч. Выяснить, выгодно или невыгодно в экономическом отношении увеличить число каналов до трех. Задания по вариантам
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
