Примеры решений задач ТВиМС. Примеры решений типовых задач

• Название: Примеры решений типовых задач
• Анкор: Примеры решений задач ТВиМС.docx
• Дата: 01.02.2017
• Размер: 478.93 Kb.
• Имя файла: Примеры решений задач ТВиМС.docx
• Тип: Решение; #1602
• страница: 7 из 11

Пример 5.2

Двумерная случайная величина распределена равномерно в круге радиуса R=1 (рис. 5.5). Определить:

а) выражение совместной плотности и функции распределения двумерной случайной величины (
X, У);

б) плотности вероятности и функции распределения одномерных составляющих Xи Y;

в) вероятность того, что расстояние от точки (
X,
Y)до начала координат будет меньше 1/3.



Решение

а) По условию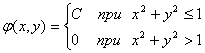



Постоянную С можно найти из соотношения (5.18):



Проще это сделать, исходя из геометрического смысла соотношения (5.18), означающего, что объем тела, ограниченного поверхностью распределения φ(х,у) и плоскостью Оху,равен 1.

В данном случае, это объем цилиндра с площадью основания πR² = π*1² = π и высотой С(рис. 5.6), равный п*С = 1, откуда С = 1/π. Следовательно,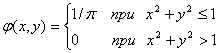



Найдем функцию распределения F(x,y) по формуле (5.17):

                                               (5.21)



Очевидно, что этот интеграл с точностью до множителя 1/π совпадает с площадью области D – области пересечения круга  с бесконечным квадрантом левее и ниже точки M(x,y) (рис.5.7).

Опустим расчеты интеграла (5.21) для различных хи у,но отметим очевидное, что

при x ≤ -1, -∞ < y < ∞ или при -∞ < х< ∞, у < -1 F(
x,
y) = 0,

так как в этом случае область D–пустая, а при x >1, у >1F(х,у)= 1, так как при этом область Dполностью совпадает с кругом х²+ у²< 1, на котором совместная плотность φ(х,у)отлична от нуля.

б) Найдем функции распределения одномерных составляющих X и
Y.По формуле (5.19) при -1< х <1





Итак,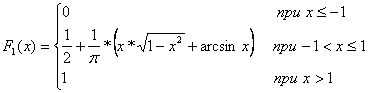



Аналогично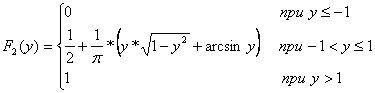



Найдем плотности вероятности одномерных составляющих Х и Y. По формуле:



График плотности φ₁(х) показан на рис. 5.8.

Аналогично



в) Искомую вероятность 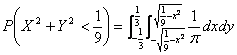, т.е. вероятность того. Что случайная точка (X,Y) будет находится в круге радиуса R₁ = 1/3 (см. рис. 5.5), можно было найти по формуле:

,

но проще это сделать, используя понятие «геометрической вероятности», т.е.


Пример 5.3

По данным примера 5.3 определить:

а) условные плотности случайных величин Xи У;

б) зависимы или независимы случайные величины Xи Y;

в) условные математические ожидания и условные дисперсии.

Решение

а) Найдем условную плотность φ
_y(x) по формуле (5.22), учитывая, что φ₂(y) ≠ 0.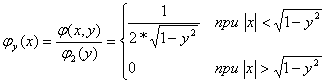


График φ
_y(x) при y= 1/2 показан на рис. 5.11.

Аналогично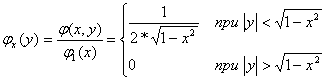



б) X и Y–независимые случайные величины, так как φ(x,y) ≠
φ₁(x)φ₂(y) или φ_y(x) ≠ φ₁(x), φ_х(y) ≠ φ₂(y).

в) Найдем условное математическое ожидание M_x(Y), учитывая, что .



Аналогично

Этот результат очевиден в силу того, что круг x² + y² ≤ 1 (рис.5.5) симметричен относительно координатных осей. Таким образом, линия регрессии Yпо
X совпадает с осью Ох (М_х(Y) = 0), а линия регрессии X по Y – с осью Оу (М_у(Х) = 0).

Найдем условную дисперсию D_x(Y):





(Тот же результат можно получить проще – по формуле дисперсии равномерного закона распределения: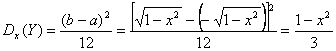

)

Аналогично

Таким образом, по мере удаления от начала координат дисперсия условных распределений уменьшается от 1/3 до 0.
Пример 5.4

По данным примера 5.2 определить ковариацию и коэффициент корреляции случайных величин Х и
Y.

Решение

В примере 5.2 были получены следующие законы распределения одномерных случайных величин:

X:	xi	1	2
	pi	0,8	0,2

и

Y:	yj	-1	0	1	2
	pj	0,2	0,3	0,3	0,2

Найдем математические ожидания и средние квадратические отклонения этих случайных величин:





, 





, 

Для нахождения математического ожидания M(
XY)произведения случайных величин Xи Yможно было составить закон распределения произведения двух дискретных случайных величин (с вероятностями его значений из табл. 5.2), а затем по нему найти M(
XY)

Закон распределения(XY)имеет вид:

(х y)k	-2	-1	0	1	2	4
pk	0,1	0,1	0,3	0,3	0,15	0,05

Но делать это вовсе не обязательно. M(
XY)Можно найти непосредственно по табл. 5.2 распределения двумерной случайной величины (
X,
Y)по формуле:

,

где двойная сумма означает суммирование по всем nm клеткам таблицы (n – число строк, m – число столбцов):



Вычислим ковариациюK_xy по формуле:

K_xy =  – a_xa_y = 0,5-1,2*0,5 = -0,1.

Вычислим коэффициент корреляции ρ по формуле:

т.е. между случайными величинами Xи Yсуществует отрицательная линейная зависимость; следовательно, при увеличении (уменьшении) одной из случайных величин другая имеет некоторую тенденцию уменьшаться (увеличиваться).
Пример 5.5

По данным примера 5.3 определить:

а) ковариацию и коэффициент корреляции случайных величин Xи Y;

б) коррелированы или некоррелированы эти случайные величины.

Решение

а) Вначале найдем математические ожидания а_х= М{Х)и a_y=
M(
Y) по формулам:



Аналогично а_у= 0 (то, что а_х= а_у= 0, очевидно из соображения симметрии распределения в круге, из которой следует, что центр его массы лежит в начале координат).

По формуле (5.34) ковариация: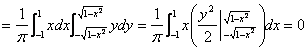





Соответственно коэффициент корреляции .

б) Так как р = 0, то случайные величины Xи
Yнекоррелированы. Убеждаемся в том, что из некоррелированности величин еще не вытекает их независимость.