Примеры решений задач ТВиМС. Примеры решений типовых задач

• Название: Примеры решений типовых задач
• Анкор: Примеры решений задач ТВиМС.docx
• Дата: 01.02.2017
• Размер: 478.93 Kb.
• Имя файла: Примеры решений задач ТВиМС.docx
• Тип: Решение; #1602
• страница: 3 из 11

3 ГЛАВА

Случайные величины

В главе рассматриваются:

- понятие случайной величины, непрерывной случайной величины;

- закон распределения дискретной случайной величины;

- математическое ожидание дискретной случайной величины;

- дисперсия дискретной случайной величины;

- функция распределения случайной величины;

- плотность вероятности;

- мода, медиана, квантили и моменты случайных величин.
Типовые задачи
Пример 3.1

По многолетним статистическим данным известно, что вероятность рождения мальчика равна 0,515. Составить закон распределения случайной величины X– числа мальчиков в семье из 4 детей. Найти математическое ожидание и дисперсию этой случайной величины.

Решение

Число мальчиков в семье из п= 4 представляет случайную величину Хсмножеством значений X= т =0, 1, 2, 3, 4, вероятности которых определяются по формуле Бернулли:

, где q = 1-p

В нашем случае n = 4, p = 0,515, q = 1-p = 0,485

Вычислим

;

;

;

;

.

(Здесь учтено, что  = 1,  = 4, , ,  = 1)
Ряд распределения имеет вид

X = m	xi	0	1	2	3	4
	pi	0,055	0,235	0,375	0,265	0,070

Убеждаемся, что 

Математическое ожидание М{Х)и дисперсию D(X)можно найти, как обычно, по формулам (3.3) и (3.11). Но в данном случае, учитывая, что закон распределения случайной величины X биномиальный, можно воспользоваться простыми формулами (4.2) и (4.3):

M(X) = np = 4*0,515 = 2,06,

D(X) = npq = 4*0,515*0,485 = 0,999.
Пример 3.2

Радист вызывает корреспондента, причем каждый последующий вызов производится лишь в том случае, если предыдущий вызов не принят. Вероятность того, что корреспондент примет вызов, равна 0,4. Составить закон распределения числа вызовов, если:

а) число вызовов не более 5;

б) число вызовов не ограничено.

Найти математическое ожидание и дисперсию этой случайной величины.

Решение:

а) Случайная величина X–число вызовов корреспондента – может принимать значения 1, 2, 3, 4, 5. Обозначим событие Ai–
i-й вызов принят (i = 1, 2, 3, 4, 5). Тогда вероятность того, что первый вызов принят, P(
X=1)=
P(
A₁)=0,4.

Второй вызов состоится лишь при условии, что первый вызов не принят, т.е.



Аналогично





Пятый вызов при любом исходе (будет принят, не принят) I последний. Поэтому



(Вероятность Р(Х=5)можно найти и иначе, учитывая, что последний вызов будет или принят, или нет, т.е.

)

Ряд распределения случайной величины X имеет вид

X:	xi	1	2	3	4	5
	pi	0,4	0,24	0,144	0,0864	0,1296

Проверяем, что 

По формуле (3.3) вычислим математическое ожидание:



Так как M(X) – нецелое число, то находить дисперсию D(X) проще не по основной формуле (3.11), а по формуле (3.16), т.е. D(X) = M(X²) – а².

Вычислим



Теперь D(X) = 7,2784 – 2,3056² = 1,9626

б) Так как число вызовов не ограничено, то ряд распределения случайной величины Х примет вид

X:	xi	1	2	3	4	…	n	…
	pi	0,4	0,24	0,144	0,0864	…	0,6n-1*0,4	…

Проверяем, что



(использовали формулу суммы сходящегося (│q│< 1) геометрического ряда:  при a = 1, q= 0,6)

По формуле (3.4) вычислим математическое ожидание



Для вычисления суммы полученного ряда воспользуемся формулой: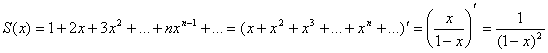



(т.е. сумма данного ряда является производной сходящегося геометрического ряда при│q│=│x│<1). При х = 0,6.

,  т.е. M(
X) = 0,4*6,25 = 2,5

По формуле (3.12) вычислим дисперсию: D(X) = M(
X²) –
a².

Вначале найдем



Для вычисления суммы полученного ряда рассмотрим сумму ряда

S₁(x) при │х│< 1: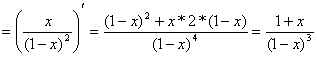





S₁(x) при х = 0,6:

,  т.е. M(X²) = 0,4*25=10

Теперь D(X) = 10-2,5² = 3,75

Пример 3.3

Среди 10 изготовленных приборов 3 неточных. Составить закон распределения числа неточных приборов среди взятых наудачу четырех приборов. Найти математическое ожидание и дисперсию этой случайной величины.

Решение

Случайная величина X– число неточных приборов среди четырех отобранных – может принимать значения i - 0, 1, 2, 3.

Общее число способов выбора 4 приборов из 10 определяется числом сочетаний . Число способов выбора четырех приборов, среди которых i неточных приборов и 4-i точных (i = 0, 1, 2, 3), по правилу произведения определится произведением числа способов выбора iнеточных приборов из 3 неточных  на число способов выбора 4-i точных приборов из 7 точных , т.е. *. Согласно классическому определению вероятности

 (i = 0, 1, 2, 3).

Учитывая, что  = 1,  = 3,  =  = 3,  = 1,

, , ,

.

Вычислим



т.е. ряд распределения будет такой:

X:	xi	0	1	2	3
	pi	1/6	1/2	3/10	1/30

Убеждаемся в том, что 

Математическое ожидание M(
X) и дисперсию D(
X)вычисляем по формулам (3.3) и (3.16):

,

  и

.
Пример 3.4

Ряд распределения дискретной случайной величины состоит из двух неизвестных значений. Вероятность того, что случайная величина примет одно из этих значений, равна 0,8. Найти функцию распределения случайной величины, если ее математическое ожидание равно 3,2, а дисперсия 0,16.

Решение

Ряд распределения имеет вид

X:	xi	x1	x2
	pi	0,8	0,2

, 
где p_i = 0,8, а p₂ = 1-p₁ = 1-0,8 = 0,2.

По условию



или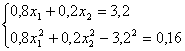



Решая полученную систему, находим два решения:

             и          

Записываем выражение функции распределения:

                   или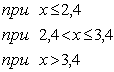                 
Пример 3.5

Рабочий обслуживает 4 станка. Вероятность того, что в течение часа станок не потребует внимания рабочего, для первого станка равна 0,9, для второго – 0,8, для третьего -0,75 и для четвертого – 0,7. Составить закон распределения случайной величины X–числа станков, которые не потребуют внимания рабочего в течение часа.

Решение

Задача может быть решена несколькими способами.

Первый способ: Пусть  – событие, состоящее в том, что k-й станок не потребует (потребует) внимания рабочего в течении часа. Тогда, очевидно:

;



.

Аналогично находим

;



,

т.е. закон (ряд) распределения случайной величины Х имеет вид:

X:	xi	0	1	2	3	4
	pi	0,0015	0,0275	0,1685	0,4245	0,378

                        (3.38)
Второй способ состоит в том, что заданы законы (ряды) распределения альтернативных случайных величин X_k (
k=1,2,3,4), выражающих число станков, не потребующих внимания рабочего в течение часа (это число для каждого станка равно 1, если этот станок не потребует внимания рабочего, и равно 0, если потребует):

X₁:                                          X₂:                                           X₃:                                          X₄:

xi	0	1		xi	0	1		xi	0	1		xi	0	1
pi1	0,1	0,9		pi2	0,2	0,8		pi3	0,25	0,75		pi4	0,3	0,7

Необходимо найти закон распределения суммы этих случайных величин, т.е. Х = Х₁ + Х₂ + Х₃ + Х₄. Суммируя последовательно Х₁ + Х₂ =Z, Х₁ + Х₂ + Х₃ = Z + X₃ = U, Х₁ + Х₂ + Х₃ + Х₄ = U + X₄ = X, получим

Z = Х₁ + Х₂:

zi	0	1	2
pi	0,02	0,26	0,2

U = Z + X₃:

um	0	1	2	3
pm	0,005	0,08	0,375	0,54

и, наконец, распределение X = U + X₄, т.е. получили (3.38).

Третий способ: Распределение Х можно получить чисто механически, перемножив биномы (двучлены):

,                             (3.39)

причем каждый из пяти полученных коэффициентов при z^k(k= 0, 1, 2, 3, 4) в функции φ₄(
z) будет выражать соответствующие вероятности P(
X=
k). Действительно, преобразовав (3.39), получим 

,

где коэффициенты – это вероятности значений случайной величины Х (3.38).