Примеры решений задач ТВиМС. Примеры решений типовых задач
 Скачать 478.93 Kb. Скачать 478.93 Kb.
|
|
Решение 1. а) По формулам (4.26) и (4.30) запишем , б) Доля костюмов 4-го роста (176 – 182 см.) в общем объеме производства определится по формуле (4.32) как вероятность (рис. 4.13), так как по (4.33) , Долю костюмов 3-го роста (170–176 см) можно было определить аналогично по формуле (4.32), но проще это сделать по формуле (4.34), если учесть, что данный интервал симметричен относительно математического ожидания а= М(Х)=173, т.е. не равенство 170 < X<176 равносильно неравенству |Х- 173| ≤3: (рис. 4.13). в) Квантиль X0,7 случайной величины Xнайдем из уравнения (3.29) с учетом (4.30): 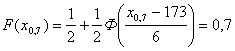 , ,откуда . По табл. II приложений находим t = 0,524 и Х0,7 = 6*t + 173 = 6*0,524 + 173 ≈ 176 (см). Это означает, что 70% мужчин данной возрастной группы имеют рост до 176 см. 10%-ная точка – это квантиль X0,9 = 181 см (находится аналогично), т.е. 10% мужчин имеют рост не менее 181 см. 2. Практически достоверно, что рост мужчин данной возрастной группы заключен в границах от a-3σ = 173-3*6 = 155 до a + 3σ = 173 + 3*6 = 191 (см), т.е. 155 ≤ Х ≤ 191 (см). Задания 4.1. Вероятность выигрыша по облигации займа за все время его действия равна 0,1. Составить закон распределения числа выигравших облигаций среди приобретенных 19. Найти математическое ожидание, дисперсию, среднее квадратическое отклонение и моду этой случайной величины. 4.2. По данным примера 4.11 найти математическое ожидание, дисперсию и среднее квадратическое отклонение доли (частости) выигравших облигаций среди приобретенных. Составить функцию распределения случайной величины, имеющей биномиальный закон распределения с параметрами n и р. 4.3. Устройство состоит из 1000 элементов, работающих независимо один от другого. Вероятность отказа любого элемента в течение времени tравна 0,002. Необходимо: а) составить закон распределения отказавших за время tэлементов; б) найти математическое ожидание и дисперсию этой случайной величины; в) определить вероятность того, что за время t откажет хотя бы один элемент. 4.4. Вероятность поражения цели равна 0,05. Производится стрельба по цели до первого попадания. Необходимо: а) составить закон распределения числа сделанных выстрелов; б) найти математическое ожидание и дисперсию этой случайной величины; в) определить вероятность того, что для поражения цели потребуется не менее 5 выстрелов. 4.5. В магазине имеются 20 телевизоров, из них 7 имеют дефекты. Необходимо: а) составить закон распределения числа телевизоров с дефектами среди выбранных наудачу пяти; б) найти математическое ожидание и дисперсию этой случайной величины; в) определить вероятность того, что среди выбранных нет телевизоров с дефектами. 4.6. Цена деления шкалы измерительного прибора равна 0,2. Показания прибора округляют до ближайшего целого числа. Полагая, что при отсчете ошибка округления распределена по равномерному закону, найти: 1) математическое ожидание, дисперсию и среднее квадратическое отклонение этой случайной величины; 2) вероятность того, что ошибка округления: а) меньше 0,04; б) больше 0,05. 4.7. Среднее время безотказной работы прибора равно 80 ч. Полагая, что время безотказной работы прибора имеет показательный закон распределения, найти: а) выражение его плотности вероятности и функции распределения; б) вероятность того, что в течение 100 ч прибор не выйдет из строя. 4.8. Текущая цена акции может быть смоделирована с помощью нормального закона распределения с математическим ожиданием 15 ден. ед. и средним квадратическим отклонением 0,2 ден. ед. 1. Найти вероятность того, что цена акции: а) не выше 15,3 ден. ед.; б) не ниже 15,4 ден. ед.; в) от 14,9 до 15,3 ден. ед. 2. С помощью правила трех сигм найти границы, в которых будет находиться текущая цена акции. 4.9. Цена некой ценной бумаги нормально распределена. В течение последнего года 20% рабочих дней она была ниже 88 ден. ед., а 75% – выше 90 ден. ед. Найти: а) математическое ожидание и среднее квадратическое отклонение цены ценной бумаги; б) вероятность того, что в день покупки цена будет заключена в пределах от 83 до 96 ден. ед.; в) с надежностью 0,95 определить максимальное отклонение цены ценной бумаги от среднего (прогнозного) значения (по абсолютной величине). 4.10. Коробки с конфетами упаковываются автоматически. Их средняя масса равна 540 г. Известно, что масса коробок с конфетами имеет нормальное распределение, а 5% коробок имеют массу, меньшую 500 г. Каков процент коробок, масса которых: а) менее 470 г; б) от 500 до 550 г; в) более 550 г; г) отличается от средней не более, чем на 30 г (по абсолютной величине)? 4.11. Случайная величина Xимеет нормальное распределение с математическим ожиданием а= 25. Вероятность попадания Хвинтервал (10; 15) равна 0,09. Чему равна вероятность попадания Xв интервал: а) (35;40); б) (30;35)? 4.12. Нормально распределенная случайная величина имеет следующую функцию распределения: F(x) = 0,5 + 0,5Ф(x-1). Из какого интервала (1;2) или (2;6) она примет значение с большей вероятностью? 4.13. Квантиль уровня 0,15 нормально распределенной случайной величины Xравен 12, а квантиль уровня 0,6 равен 16. Найти математическое ожидание и среднее квадратическое отклонение случайной величины. 4.14. 20%-ная точка нормально распределенной случайной величины равна 50, а 40%-ная точка равна 35. Найти вероятность того, что случайная величина примет значение в интервале (25;45). 4.15. Месячный доход семей можно рассматривать как случайную величину, распределенную по логнормальному закону. Полагая, что математическое ожидание этой случайной величины равно 1000 ден. ед., а среднее квадратическое отклонение 800 ден. ед., найти долю семей, имеющих доход: а) не менее 1000 ден. ед.; б) менее 500 ден. ед. 4.16. Известно, что нормально распределенная случайная величина принимает значение: а) меньшее 248 с вероятностью 0,975; б) большее 279 с вероятностью 0,005. Найти функцию распределения случайной величины X. 4.17. Случайная величина Xраспределена по нормальному закону с нулевым математическим ожиданием. Вероятность попадания этой случайной величины на отрезок от –1 до +1 равна 0,5. Найти выражения плотности вероятности и функции распределения случайной величины X. 4.18. Имеется случайная величина X,распределенная по нормальному закону с математическим ожиданием аи дисперсией σ2. Требуется приближенно заменить нормальный закон распределения равномерным законом в интервале (а; р); границы а, р подобрать так, чтобы сохранить неизменными математическое ожидание и дисперсию случайной величины X. 4.19. Случайная величина Xраспределена по нормальному закону с математическим ожиданием а= 0. При каком значении среднего квадратического отклонения овероятность попадания случайной величины Xв интервал (1;2) достигает максимума? 4.20. Время ремонта телевизора распределено по показательному закону с математическим ожиданием, равным 0,5 ч. Некто сдает в ремонт два телевизора, которые одновременно начинают ремонтировать, и ждет, когда будет отремонтирован один из них. После этого с готовым телевизором он уходит. Найти закон распределения времени: а) потраченного клиентом; б) которое должен потратить клиент, если он хочет забрать сразу два телевизора. 5 ГЛАВА Многомерные случайные величины В главе рассматриваются: - понятие многомерной случайной величины и ее закон распределения; - функция распределения многомерной случайной величины; - плотность вероятности двумерной случайной величины; - ковариация и коэффициент корреляции. Типовые задачи Пример 5.1 Закон распределения дискретной двумерной случайной величины (Х, Y) задан в табл. 5.2. Таблица 5.2
Найти: а) законы распределения одномерных случайных величин Xи Y; б) условные законы распределения случайной величины Xпри условии Y = 2 и случайной величины Yпри условии X= 1; в) вычислить P( Y< X). Решение а) Случайная величина Xможет принимать значения: Х =1 с вероятностью P1= 0,10 + 0,25 + 0,30 + 0,15 = 0,8; X= 2с вероятностью P2 = 0,10 + 0,05 + 0,00 + 0,05 = 0,2, т.е. ее закон распределения
Аналогично закон распределения
б) Условный закон распределения Х при условии, что Y = 2. получим, если вероятность pij , стоящие в последнем столбце табл.5.2, разделим на их сумму, т.е. p(Y= 2) = 0,2. Получим
Аналогично для получения условного закона распределения Y при условии Х = 1 вероятности pij, стоящие в первой строке табл. 5.2, делим на их сумму, т.е. на p(X = 1) = 0,8. Получим
в) Для нахождения вероятностей Р(Y< Х) складываем вероятности событий pij из табл. 5.2, для которых yj< х i. Получим Р(Y< Х) = 0,10 + 0,25 + 0,10 + 0,05 + 0,00 = 0,5 |
