Примеры решений задач ТВиМС. Примеры решений типовых задач

• Название: Примеры решений типовых задач
• Анкор: Примеры решений задач ТВиМС.docx
• Дата: 01.02.2017
• Размер: 478.93 Kb.
• Имя файла: Примеры решений задач ТВиМС.docx
• Тип: Решение; #1602
• страница: 8 из 11

Пример 5.6

Найти плотность вероятности случайной величины Y = 1-X³, где случайная величина Xраспределена по закону Коши с плотностью вероятности

.

Решение

По условию y = f(x) = 1-x³, откуда . Производная (по абсолютной величине):

.

Плотность вероятности:


Пример 5.7

Найти математическое ожидание и дисперсию случайной величины Y = 2-3sinX, если плотность вероятности случайной величины Xестьφ(х) = cosX на отрезке [-π/2, π/2].

Решение

По формуле (5.57)





Дисперсия D(Y) = M(Y²) – :

.
Пример 5.8

Найти закон распределения суммы двух случайных величин, распределенных равномерно на отрезке [0; 1].

Решение

Пусть Z=
X+
Y,где φ₁(x)= 1 при 0 ≤ х≤1 и
φ₂(у)= 1 при 0 ≤ у≤1.

По формуле (5.49) плотность вероятности:



Если z < 0, то для 0 ≤ x≤ 1  z-x< 0; если z > 2, то для 0 ≤ x≤ 1  z-x> 1, следовательно, в этих случаях φ₂(z-x) = 0 и φ(z) = 0.

Пусть 0 ≤ z ≤ 2. Подынтегральная функция φ₂(z-x) будет отлична от нуля только для значений х, при которых 0 ≤ z-
x≤ 1 или, что то же самое, при  z-1 ≤ x≤ z.

Если 0 ≤ z≤ 1, то .

Если 1 ≤ z≤ 2, то .

Объединяя все случаи, получим: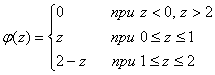

                                                       (5.60)

Закон распределения (5.60) называется законом распределения Симпсонаили законом равнобедренного треугольника(рис. 5.16).

Вычисление φ(z) можно было провести и иначе: вначале найти функцию распределения F(
z),а затем – ее производную, т.е. φ(z) = F'(z). Преимущество такого подхода состоит в возможности использования геометрической интерпретации функции F(z) как площади S_Dобласти D– части квадрата (со стороной, равной 1), лежащей левее и ниже прямой у =z- х(рис. 5.17).

Действительно (см. рис. 5.17), при 0 ≤ z≤1 S_D= z²/2(площадь заштрихованного треугольника со стороной z), а при 1 ≤ z ≤ 2 S_D = 1 - (2 -z)²/2 (площадь квадрата без площади незаштрихованного треугольника, сторона которого, как нетрудно показать, равна (2 – z).Следовательно,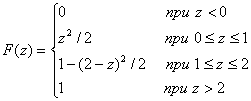



и выражение (5.60) для φ(
z)получается дифференцированием F(z).


Задания
5.1.      Закон распределения двумерной дискретной случайной величины (
X,
Y)задан в табл. 5.3.

Таблица 5.3

yi xi	0	1	2	3
-1	0,02	0,03	0,09	0,01
0	0,04	0,20	0,16	0,10
1	0,05	0,10	0,15	0,05

Найти:

а) законы распределения одномерных случайных величин Х и
Y;

б) условные законы распределения случайной величины Xпри условии Y=2 и случайной величины Y при условии Х =1;

в) вероятность P(Y > X).

5.2.      Рассматривается двумерная случайная величина (
X,
Y),где X–поставка сырья, Y–поступление требования на него. Известно, что поступление сырья и поступление требования на него могут произойти в любой день месяца (30 дней) с равной вероятностью. Определить:

а) выражение совместной плотности и функции распределения двумерной случайной величины (Х,У),

б) плотности вероятности и функции распределения одномерных составляющих Xи Y;

в) зависимы или независимы Xи Y;

г) вероятности того, что поставка сырья произойдет до и после поступления требования.

5.3.      Двумерная случайная величина (
X,
Y)распределена равномерно внутри квадрата Rс центром в начале координат. Стороны квадрата равны корень2и составляют углы 45° с осями координат. Определить:

а) выражение совместной плотности двумерной случайной величины (
X,
Y);

б) плотности вероятности одномерных составляющих Xи Y;

в) их условные плотности;

г) зависимыили независимы Х и
Y.

5.4.      Даны плотности вероятности независимых составляющих двумерной случайной величины (
X,
Y):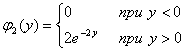

                            

Найти выражение совместной плотности и функции распределения двумерной случайной величины.

В примерах 5.14–5.16 определить:

а) ковариацию и коэффициент корреляции случайных величин Xи Y,

б) коррелированы или некоррелированы эти случайные величины.

5.5.     Использовать данные примера 5.10.

5.6.     Использовать данные примера 5.11.

5.7.     Использовать данные примера 5.12.

5.8.     Случайная величина Xраспределена на всей числовой оси с плотностью вероятности φ(х) = 0,5е^-│Х│. Найти плотность вероятности случайной величины Y=
X²и ее математическое ожидание.

5.9.     Найти закон распределения суммы двух независимых случайных величин, каждая из которых распределена по стандартному нормальному закону, т.е. N(0,1).

5.10. Двумерная случайная величина определяется следующим образом. Если при подбрасывании игральной кости выпадает четное число очков, то Х =1, в противном случае X= 0;
Y=1, когда число очков кратно трем, в противном случае Y=0. Найти:

а) законы распределения двумерной случайной величины (
X,
Y) и ее одномерных составляющих;

б) условные законы распределения Хи
Y.

5.11. Двумерная случайная величина (
X,
Y)распределена с постоянной совместной плотностью внутри квадрата ОАВС,где O(0;0), A(0;1), B(1;1), С(1;0). Найти выражение совместной плотности и функции распределения двумерной случайной величины (
X,
Y).

5.12.  Поверхность распределения двумерной случайной величины (
X,
Y)представляет прямой круговой конус, основанием которого служит круг с центром в начале координат и с радиусом 1. Вне этого круга совместная плотность двумерной случайной величины (
X,
Y)равна нулю. Найти выражения совместной плотности φ(х, у),плотностей вероятностей одномерных составляющих φ₁(x), φ₂ (y), условных плотностей φ
_x(y),
φ
y(x). Выяснить, являются ли случайные величины Xи Y.зависимыми; коррелированными.

5.13.  Двумерная случайная величина (
X,
Y)распределена по закону

Найти:

а) коэффициент А;

б) вероятность попадания случайной величины (
X,
Y)в пределы квадрата, центр которого совпадает с началом координат, а стороны параллельны осям координат и имеют длину 2.

Установить, являются ли величины X и Y зависимыми; найти φ₁(х),
φ₂(
y).

5.14.  Совместная плотность двумерной случайной величины (
X, У)имеет вид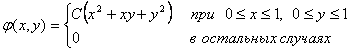



Найти:

а) постоянную С;

б) плотности вероятности одномерных составляющих;

в) их условные плотности;

г) числовые характеристики а_х, а_у,
D(Х),
D(
Y), ρ.

5.15.  Найти совместную плотность двумерной случайной величины (
X,
Y)и вероятность ее попадания в область D–прямоугольник, ограниченный прямыми х = 1,х = 2,у =3,у =5,если известна ее функция распределения (
X,
Y):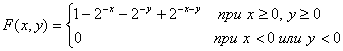



5.16.  Задана совместная плотность двумерной случайной величины (X,
Y):

.

Найти функцию распределения F(x,y).

5.17.  Имеются независимые случайные величины XиY.Случайная величина X распределена по нормальному закону с параметрами а_х = 0, . Случайная величина Yраспределена равномерно на интервале (0;1). Найти выражения совместной плотности и функции распределения двумерной случайной величины (X,
Y).

5.18.  Совместная плотность двумерной случайной величины (X,
Y)задана формулой:


Найти a_x, a_y, , , ρ.

5.19.  Независимые случайные величины X,
Yраспределены по нормальным законам с параметрами a_x = 2, a_y = -3,  = 1,  = 4. Найти вероятности событий:

а) (X< a_x)(Y< a_y);

б) Y < X-5;

в)(│X│< 1)(│Y│< 2).

5.20.  Задана плотность вероятности φ(х) случайной величины Х, принимающей только положительные значения. Найти плотность вероятности случайной величины Y, если:

а) Y = e^-
x;

б) Y = lnX;

в) Y = X³;

г) Y = 1/X²;

д) Y = .

5.21.  Случайная величина Х равномерно распределена в интервале (-π/2; π/2). Найти плотность вероятности случайной величины Y =sinX.

5.22.  Случайная величина распределена по закону Релея с плотностью вероятности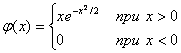



Найти закон распределения случайной величины Y = .

5.23.  Случайная величина Х распределена по закону Коши с плотностью вероятности

.

Найти плотность вероятности обратной величины Y = 1/X.

5.24.  Дискретная случайная величина Х имеет ряд распределения

xi	-1	0	1	2
pi	0,2	0,1	0,3	0,4

Найти математическое ожидание и дисперсию случайной величины
Y= 2^х

5.25.  Имеются две случайные величины Xи Y,связанные соотношением Y= 2 – ЗХ.Числовые характеристики случайной величины Xзаданы а_х= -1; D(
X) =4. Найти:

а) математическое ожидание и дисперсию случайной величины Y;

б) ковариацию и коэффициент корреляции случайной величин Х и
Y.

5.26.  Случайная величина Xзадана плотностью вероятности φ(x) = cosx в интервале (0, π/2); вне этого интервала φ(x) = 0. Найти математическое ожидание случайной величины Y=
X².

5.27.  Случайная величина Xраспределена с постоянной плотностью вероятности в интервале (1;2) и нулевой плотностью вне этого интервала. Найти математическое ожидание и дисперсию случайной величины Y=1/x

5.28.  Непрерывная случайная величина Xраспределена в интервале (0;1) по закону с плотностью вероятности



Найти математическое ожидание и дисперсию случайной величины Y=
X².

5.29.  Непрерывная случайная величина распределена по показательному закону с параметром Х = 2.Найти математическое ожидание и дисперсию случайной величины Y=
e^-
X.

5.30.  Случайная величина Xраспределена по нормальному закону с параметрами а= 0, σ²= 5. Найти математическое ожидание случайной величины Y=1 - ЗХ²+ 4Х³.

5.31.  Имеются две независимые случайные величины Xи
Y.Величина Xраспределена по нормальному закону с параметрами а_х=1,  = 4. Величина Yраспределена равномерно в интервале (0;2). Найти:

а) М(Х - У),
D(Х -
Y);

б) M(
X²),
M(
Y²).