научка проценты 2022. Процентные вычисления в нашей жизни
 Скачать 0.65 Mb. Скачать 0.65 Mb.
|
|
Костанайская область Денисовский район Свердловская средняя школа Тема: «Процентные вычисления в нашей жизни» Секция: математика Выполнил: Григорьев Андрей 10 класс ГУ «Свердловская средняя школа» Научный руководитель: Кононова Г.Н. Научный консультант: кандидат физико – математических наук, доцент КГПИ Калжанов М.У. 2015г. Оглавление: I. Абстракт …………………………………………………………… 3 стр. II. Введение…………………………………………………………... 4 - 5 стр. III. Исследовательская часть: Глава 1. Проценты в прошлом и настоящем. 1.1. История возникновения процентов…………………………….. 6 – 7 стр. 1.2. Простые и сложные проценты…………………………………. 7 – 8 стр. 1.3. Результаты опроса о роли процентов в современной жизни… 8 - 9 стр. Глава 2. Виды задач на проценты и способы их решения. 2.1. Виды задач на проценты……………………………………….. 9 - 10 стр. 2.2. Решение задач на проценты составлением пропорции……… 10 стр. 2.3. Решение задач на проценты алгебраическим методом……… 10 - 11 стр. 2.4. Решение задач на концентрацию и процентное содержание…. 11 – 12 стр. Глава 3. Применение процентов в разных сферах жизни человека. 3.1.Банковские операции и расчеты………………………………. 12 – 13 стр. 3.2. Использование процентов людьми разных профессий……... 13 – 15 стр. 3.3. Проценты в повседневной жизни……………………………. 16 – 17 стр. 3.4.Процентные вычисления в жизни нашей школы…………… 17 – 18 стр. IV. Заключение………………………………………………….. 18 стр. V. Список литературы…………………………………………. 19 стр. VI. Аннотация…………………………………………………... 20 стр. Приложения……………………………………………………... 21 – 25 стр. Абстракт Выбор данной темы обусловлен тем, что знания о процентных вычислениях необходимы каждому человеку для жизни в современном обществе. Многие жизненные ситуации требуют знания вычисления процентов: получение кредитов в банке, вклады сбережений, покупка товара в кредит, расчёты налогообложений, расчёты скидок в процентном соотношении и т.д. Изучение этой темы кажется нам интересным для исследования по той причине, что наглядно отражает применение процентов в повседневной жизни. Цель исследования заключалась в расширении знаний о применении процентных вычислений для решения большого круга задач и в разных сферах жизни человека. В качестве гипотезы выступает предположение о том, что, если изучить литературу по данному вопросу, провести социальный опрос у людей различных специальностей на предмет использования процентов в различных сферах деятельности, то можно выявить значимость процентных вычислений. Объект исследования: процент, различные виды задач на проценты, решение задач на проценты людьми разных профессий. Процедура исследования состояла из следующих этапов: 1) Определение целей и задач исследования. 2) Изучение теоретического материала и построение гипотезы исследования. 3) Выбор методов исследования, проведение исследовательской работы. 4)Анализ и оформление результатов исследования. Новизна исследования состоит в том, что в работе рассматриваются сведения, которые не изучаются в школьном курсе математики и впервые тема обобщается на местном материале. В качестве методов исследования применялись: 1) сравнительный анализ литературы, 2) систематизация и сбор информации, 3) построение диаграмм, 4) обобщение результатов исследования. Практическая значимость работы состоит в возможности использовании материала и результатов данного исследования на уроках математики, факультативных занятиях и прикладных курсах, а так же при подготовке учащихся к ЕНТ. «Математике должно учить в школе ещё с той целью, чтобы познания, здесь приобретаемые, были достаточными для обыкновенных потребностей в жизни» И.Л. Лобачевский II. Введение. Проценты в нашей жизни. Актуальность нашей работы в том, что понимание процентов и умение выполнять процентные расчеты необходимы каждому человеку для применения в практической деятельности и различных жизненных ситуациях. Цель исследования: рассмотреть общий подход к решению задач на проценты, которые встречаются в разных сферах жизнедеятельности человека, сформировать понимание необходимости знаний процентных вычислений для решения большого круга задач, научиться применять знания о процентах в повседневной жизни. Задачи исследования: Выяснить историю происхождения процентов; Найти самые разнообразные задачи с процентами, выяснить их методы решения. Выяснить сферы использования процентов, их роль в жизни человека. Используемые методы и приемы: 1. Поиск информации о процентах в различных источниках: библиотеке, интернете, газетах, учебниках. 2. Сравнение и обобщение информации. 3. Социологический опрос и анкетирование. 4. Анализ собранной информации. Современная жизнь делает задачи на проценты актуальными, так как сфера практического приложения процентных расчетов расширяется. Вопросы инфляции, повышение цен, рост стоимости акций, снижение покупательской способности касаются каждого человека в нашем обществе. Планирование семейного бюджета, выгодного вложения денег в банки, невозможны без умения производить несложные процентные вычисления. Без понятия «процент» нельзя обойтись ни в бухгалтерском учёте, ни в финансовом анализе, ни в статистике. Проценты – математическое понятие, которое часто встречается в повседневной жизни. Любой человек должен уметь решать задачи, предлагаемые самой жизнью. Мы платим налоги. Как посчитать материальное вознаграждение, которое получаем мы, когда кладем деньги на депозит, какое вознаграждение получает банк, когда мы берем кредит, ипотеку. Все эти вопросы решает знание процентов. Везде – в газетах, по радио, телевидению и на работе обсуждаются повышение цен, зарплат, пенсии, рост стоимости акций, снижение покупательской способности населения. Так, мы часто слышим или читаем, что, например, цены повысились на 20%, молоко содержит 4% жира, пенсия повысилась на 10%, в выборах приняли участие 76 % избирателей. Чтобы начислить зарплату работнику, нужно знать процент налоговых отчислений; чтобы открыть депозитный счёт в сбербанке, нужно знать размеры процентных начислений на сумму вклада; чтобы знать приблизительный рост цен в будущем году, мы интересуемся процентом инфляции. Решение математических задач практического содержания позволяет убедиться в значении математики для различных сфер человеческой деятельности, увидеть широту возможных приложений математики, понять её роль в современной жизни. Исследовательская работа направлена на повышение интереса к математике, развитие самостоятельности, развития речи; способности на основе полученных сведений и теоретических знаний создавать новые продукты на основе умений находить, анализировать, обрабатывать, оценивать и создавать информацию в разных формах. В ходе исследования перед нами стоял вопрос «Можно ли жить без знаний процентов?» В ходе работы над проектом мы получили дополнительные знания по процентным исчислениям, которые будем применять не только в учебно-познавательном процессе, но и в повседневной жизни. Исследования складываются из общения с представителями разных специальностей на тему использования ими процентов в своей профессиональной деятельности и анализа полученной информации. Умение выполнять процентные расчеты необходимо каждому человеку. Ценность полученных результатов в том, что они продемонстрировали широкий спектр применения расчёта процентов в повседневной жизни. Глава 1. Проценты в прошлом и настоящем. История возникновения процентов. Слово «процент» происходит от латинского слова “pro centum”, что означает «со ста». Идея выражения частей целого постоянно в одних и тех же долях родилась ещё в древности у вавилонян, в их клинописных табличках уже содержались задачи на расчёт процентов. Были известны проценты и в Индии, где с давних пор вёлся счёт в десятичной системе счисления. Индийские математики вычисляли проценты, применяя так называемое тройное правило, т.е. пользуясь пропорцией. Они умели производить и более сложные вычисления с применением процентов. В русском языке слово «процент» имеет и другое смысловое значение − выражает тот факт, что заёмщик помимо возврата предоставленных ему кредитором денежных средств должен дополнительно заплатить кредитору за использование этих средств. Об этом говорит, например, объявление: «Банк предоставляет населению кредиты под проценты». Денежные расчеты с процентами были особенно распространены в Древнем Риме. Римляне называли процентами деньги, которые платил должник заимодавцу за каждую сотню. Даже римский сенат вынужден был установить максимально допустимый процент, взимаемый с должника, так как некоторые заимодавцы усердствовали в получении процентных денег. От римлян проценты перешли к другим народам. В средние века в Европе в связи с широким развитием торговли особенно много внимания обращали на умение вычислять проценты. В то время приходилось рассчитывать не только проценты, но и проценты с процентов, т. е. сложные проценты, как называют их в наше время. Отдельные конторы и предприятия для облегчения труда при вычислениях процентов разрабатывали свои особые таблицы, которые составляли коммерческий секрет фирмы. В Европе десятичные дроби появились на 1000 лет позже, их ввел бельгийский ученый Симон Стевин. В 1584г. он впервые опубликовал таблицу процентов. Введение процентов было удобным для определения содержания одного вещества в другом; в процентах стали измерять количественное изменение производства товара, рост и спад цен, рост денежного дохода и т.д. Знак «%» происходит, как полагают, от итальянского слова cento(сто), которое в процентных расчётах часто писалось сокращённо cto. Отсюда путём дальнейшего упрощения буквы t в наклонную черту произошёл современный символ для обозначения процента. Другая версия происхождения этого знака заключается в том, что в Париже в 1685 году наборщик книги-руководства по коммерческой арифметике допустил опечатку – вместо cto написал %. Долгое время под процентами понимались исключительно прибыль или убыток на каждые 100 рублей. Они применялись только в торговых и денежных сделках. Уже в далекой древности широко было распространено ростовщичество - выдача денег под проценты. Разность между той суммой, которую возвращали ростовщику, и той, которую первоначально взяли у него, называлась лихвой. Так, в Древнем Вавилоне она составляла 20 % и более! Известно, что в XIV-XV вв. В Западной Европе широко распространились банки - учреждения, которые давали деньги в долг князьям, купцам, ремесленниками и т. д. Конечно, банки давали деньги не бескорыстно: за пользование предоставленными деньгами они брали плату, как и ростовщики древности. Эта плата выражалась обычно в виде процентов к величине выданных в долг денег. Затем область их применения расширилась, проценты встречаются в хозяйственных и финансовых расчетах, статистике, науке и технике. [9] Ныне процент - это частный вид десятичных дробей, сотая доля целого (принимаемого за единицу). Процентами очень удобно пользоваться на практике, так как они выражают части целых в одних и тех же долях. Это дает возможность упрощать расчеты и легко сравнивать части между собой и с целым. Процент – сотая доля числа, принимаемого за целое. [1] Если речь идет о проценте от данного числа, то это число и принимается за 100 %. Например, 1 % от зарплаты - это сотая часть зарплаты; 100 % зарплаты - это сто сотых частей зарплаты, т. е. вся зарплата. Сотая часть метра – это сантиметр, сотая часть центнера - это килограмм. 1% - одна сотая доля числа. Как известно из практики, с помощью процентов часто показывают изменение той или иной конкретной величины. Такая форма является наглядной числовой характеристикой изменения, характеризующей значимость произошедшего изменения. Величина, выраженная в процентах, является более наглядной, понятной, ее легко сравнить с другими значениями. 1.2. Простые и сложные проценты Увеличение вклада по схеме простых процентов характеризуется тем, что суммы процентов в течение всего срока хранения определяются исходя только из первоначальной суммы вклада (So), независимо от срока хранения и количества начисления процентов. Пример: Пусть вкладчик открыл в сберкассе счет и положил на него S0 рублей. Если банк обязуется выплачивать вкладчику в конце каждого года р% от первоначальной суммы So, тогда по истечении одного года сумма начисленных процентов cоставляет 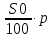 руб. и величина вклада станет равной: S = So + руб. и величина вклада станет равной: S = So + 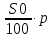 = So (1+ = So (1+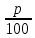 ) рублей, р% называют годовой процентной ставкой. Если через год вкладчик снимает со счёта начисленные проценты ) рублей, р% называют годовой процентной ставкой. Если через год вкладчик снимает со счёта начисленные проценты 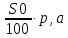 за два года начисленные проценты составят за два года начисленные проценты составят 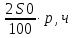 ерез n лет на вкладе по формуле простого процента будет: Sn = So (1+ ерез n лет на вкладе по формуле простого процента будет: Sn = So (1+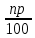 ) Рассмотрим применение этой формулы для решения задачи из тестов ЕНТ. Задача. Банк обещает своим клиентам годовой рост вклада 4%. Если человек вложит в банк 1200 тенге, то через год получит? [6] Решение: т.к. So = 1200тг, р = 4%, получим: S = 1200 (1 + ) Рассмотрим применение этой формулы для решения задачи из тестов ЕНТ. Задача. Банк обещает своим клиентам годовой рост вклада 4%. Если человек вложит в банк 1200 тенге, то через год получит? [6] Решение: т.к. So = 1200тг, р = 4%, получим: S = 1200 (1 + 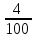 ) = 1248. Ответ: 1248 тенге. Рассмотрим другой способ расчёта банка с вкладчиком. Он состоит в следующем: если вкладчик не снимает со счёта сумму начисленных процентов, то эта сумма присоединяется к основному вкладу, а в конце следующего года банк будет начислять проценты уже на новую, увеличенную сумму. Это означает, что банк станет начислять проценты не только на основной вклад, но и на проценты, которые на него полагаются. Такой способ начисления «процентов на проценты» называют сложными процентами. Сумма вклада по формуле сложного процента: Sn=S0 (1+ ) = 1248. Ответ: 1248 тенге. Рассмотрим другой способ расчёта банка с вкладчиком. Он состоит в следующем: если вкладчик не снимает со счёта сумму начисленных процентов, то эта сумма присоединяется к основному вкладу, а в конце следующего года банк будет начислять проценты уже на новую, увеличенную сумму. Это означает, что банк станет начислять проценты не только на основной вклад, но и на проценты, которые на него полагаются. Такой способ начисления «процентов на проценты» называют сложными процентами. Сумма вклада по формуле сложного процента: Sn=S0 (1+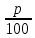 )n, где n = 1,2,3…. Рассмотрим применение формулы сложного процента для решения задач из тестовых заданий ЕНТ. Задача 1. Какая сумма будет на счете через четыре года, если на него положено 2000 тенге под 30% годовых? [6] Решение: т.к. So = 2000 тг, р = 30%, n = 4 получим: S4 = 2000· (1 + )n, где n = 1,2,3…. Рассмотрим применение формулы сложного процента для решения задач из тестовых заданий ЕНТ. Задача 1. Какая сумма будет на счете через четыре года, если на него положено 2000 тенге под 30% годовых? [6] Решение: т.к. So = 2000 тг, р = 30%, n = 4 получим: S4 = 2000· (1 +  )4 = 2000 · ( )4 = 2000 · ( )4 = 5712,2 Ответ: 5712,2 тенге. Задача 2. Каким должен быть начальный вклад, чтобы через два года вклад в банке, начисляющем 30% годовых, возрос до 845000 тенге? [6] Решение : т.к. S2 = 845000 тг, р = 30%, n = 2, получим: 845000 = S0 · ( 1 + )4 = 5712,2 Ответ: 5712,2 тенге. Задача 2. Каким должен быть начальный вклад, чтобы через два года вклад в банке, начисляющем 30% годовых, возрос до 845000 тенге? [6] Решение : т.к. S2 = 845000 тг, р = 30%, n = 2, получим: 845000 = S0 · ( 1 +  )2 )2  845000 = S0 · 1,69 845000 = S0 · 1,69  S0 = 500000 Ответ: 500000 тенге. S0 = 500000 Ответ: 500000 тенге.1.3. Результаты опроса о роли процентов в современной жизни. Для того, чтобы выявить мнение людей о роли процентных вычислений в современной жизни, мы провели анкетирование среди учащихся и учителей. В анкетировании приняли участие 82 человека. Учащимся 5 - 11 классов и учителям было предложено ответить на следующие вопросы: 1. Считаете ли необходимым умение выполнять процентные вычисления? 2. Часто ли вам приходится выполнять процентные вычисления? 3. Всегда ли вы справляетесь с выполнением процентных вычислений? 4. Можно ли обойтись в жизни без знаний процентов? Результаты проведенного анкетирования отражены в таблице (Приложение 1). По результатам проведенного опроса мы выяснили, что 90 % опрошенных людей считают необходимым выполнять процентные вычисления. 36% всегда справляются с их выполнением, а 64% - не всегда. 42% респондентов считают, что им часто приходится выполнять процентные вычисления, 48% -выполняют их редко. 98% респондентов считают, что в жизни нельзя обойтись без знаний процентов. По результатам анкетирования можно сделать вывод о большой значимости процентов в жизни человека. Глава 2. Виды задач на проценты и способы их решения. 2.1. Виды задач на проценты. Нахождение процентов от числа. Чтобы найти процент от числа, следует: 1.Проценты записать десятичной дробью. 2. Число умножить на эту десятичную дробь. Задача: В магазин привезли 14 т капусты, 70% всей капусты продали. Сколько тонн капусты осталось? [4] Решение: Оставшаяся часть капусты составляет: 100% - 70% = 30% = 0,3 14 · 0,3 = 4,2 Ответ: 4,2 тонны. Нахождение числа по его процентам. Чтобы найти число по его процентам, следует: 1. Проценты записать десятичной дробью. 2. Число разделить на эту десятичную дробь. Задача: Тракторная бригада вспахала за день 25% всего поля, что составляет 60 га. Какова площадь всего поля? [3] Решение: 25% = 0,25; 60 : 0.25 = 240 Ответ: 240 га. Нахождение процентного отношения чисел. Чтобы узнать, сколько процентов одно число составляет от второго, следует: 1. Первое число разделить на второе. 2. Результат умножить на 100%. Задача: Длина прямоугольника 40 дм, площадь 200 дм2. Сколько процентов составляет ширина от длины ? [5] Решение: ширина равна 200 : 40 = 5 5:40 ·100% = 12,5% Увеличение на р% Чтобы увеличить положительное число а на р%, следует: умножить число а на коэффициент увеличения к = (1+0,01р) Задача: Цена на яблоки выросла на 30%. Какова цена яблок после повышения, если первоначальная цена 250 тенге? [6] Решение: к = 1 + 0,01 ·30 = 1,3 250 · 1,3 = 325 Ответ: 325 тенге. Уменьшение на р% Чтобы уменьшить положительное число а на р%, следует: умножить число а на коэффициент уменьшения к = (1- 0,01·р) Задача: Цена на путевку в санаторий снизилась на 10%. Сколько стоит путевка, если ее первоначальная цена 12 рублей? [2] Решение: к = 1 – 0,01·10 = 0,9; 12 · 0,9 = 10,8 Ответ: 10,8 рубля. 2.2. Решение задач на проценты составлением пропорции. При решении задач на проценты некоторая величина b принимается за 100%, а ее часть – величинаa – принимается за x % и составляется пропорция: 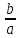 = = 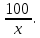 Из пропорции по двум известным величинам определяют неизвестную третью величину, пользуясь основным свойством пропорции: b·x =100·a Задача 1. В театральной студии занимаются 36 девушек. Сколько всего учащихся занимаются в данной студии, если юноши составляют 52%? [4] Решение: Девушки составляют 100% - 52% = 48% всех учащихся. Девушки: 36 чел. - 48% Всего учащихся: х чел. - 100% Из пропорции по двум известным величинам определяют неизвестную третью величину, пользуясь основным свойством пропорции: b·x =100·a Задача 1. В театральной студии занимаются 36 девушек. Сколько всего учащихся занимаются в данной студии, если юноши составляют 52%? [4] Решение: Девушки составляют 100% - 52% = 48% всех учащихся. Девушки: 36 чел. - 48% Всего учащихся: х чел. - 100%Составляем пропорцию: 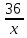 = =   х = х =  = 75 Ответ: 75 учащихся. Задача 2. Зарплату токарю повысили сначала на 10%, а затем через год еще на 20%. На сколько процентов повысилась зарплата токаря по сравнению с первоначальной? [2] Решение: а – первоначальная зарплата 1 после повышения на 10% - 1,1 а через год после повышения на 20% – 1,1 а · 1,2 = 1,32а Составим пропорцию: = 75 Ответ: 75 учащихся. Задача 2. Зарплату токарю повысили сначала на 10%, а затем через год еще на 20%. На сколько процентов повысилась зарплата токаря по сравнению с первоначальной? [2] Решение: а – первоначальная зарплата 1 после повышения на 10% - 1,1 а через год после повышения на 20% – 1,1 а · 1,2 = 1,32а Составим пропорцию:  = =   = 132, 132% - 100% = 32% Ответ: на 32%. = 132, 132% - 100% = 32% Ответ: на 32%.2.3. Решение задач на проценты алгебраическим методом. Задача 1. Одна сторона прямоугольника на 42% больше другой. Площадь прямоугольника 568 см2. Найти меньшую из сторон. [5] Решение: Пусть х – одна сторона прямоугольника, тогда вторая сторона будет 1,42 х. Составим уравнение и решим его: х · 1,42 х = 568 1,42х2 = 568 х2 = 400 х1 = 20 и х2 = - 20 – не подходит Ответ: 20 см. Задача 2. Турист прошел в первый день 40% маршрута, во второй день 45% оставшегося пути, после чего ему осталось пройти на 6 км больше, чем он прошел во второй день. Весь маршрут составляет? [6] Решение: х (км) – весь маршрут 0,4 х (км) – турист прошел в первый день пути 0,45(х – 0,4х) = 0,27х (км )– турист прошел во второй день пути х - (0,4х + 0,27х) = 0,33х (км) – осталось пройти туристу Т.к. туристу осталось пройти на 6 км больше, чем он прошел во второй день, составим уравнение и решим его: 0,33х – 0,27х = 6 0,06х = 6 х = 100 Ответ: 100 км. 2.4. Решение задач на концентрацию и процентное содержание. Для решения задач из этого раздела введем основные понятия: Пусть даны два различных вещества А и В с массами mА и mВ. Масса смеси, составленной из этих веществ, равна М = mА + mВ. Массовая концентрация вещества А в смеси (доля чистого вещества в смеси) СА =  = =  . Массовые концентрации связаны равенством: СА+ СВ =1 Процентное содержание вещества А в данной смеси вычисляется по формуле: РА = СА · 100% Задача 1. Имеется 50г раствора, содержащего 8% соли. Надо получить 5% -й раствор. Чему равна масса пресной воды, которую необходимо добавить к первоначальному раствору? [5] Решение: Пусть требуется добавить х кг пресной воды. За чистое вещество принимаем соль. Решение оформим таблицей. . Массовые концентрации связаны равенством: СА+ СВ =1 Процентное содержание вещества А в данной смеси вычисляется по формуле: РА = СА · 100% Задача 1. Имеется 50г раствора, содержащего 8% соли. Надо получить 5% -й раствор. Чему равна масса пресной воды, которую необходимо добавить к первоначальному раствору? [5] Решение: Пусть требуется добавить х кг пресной воды. За чистое вещество принимаем соль. Решение оформим таблицей.
Составим уравнение: 0,08 · 50 = (50 + х) · 0,05 50 + х = 80 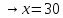 Ответ: 30 кг. Задача 2. В растворе содержится 15% соли. Если добавить 150г соли, то в растворе будет содержаться 45% соли. Найти массу соли в первоначальном растворе. [5] Решение: Пусть масса раствора -х г. Решение оформим таблицей. Ответ: 30 кг. Задача 2. В растворе содержится 15% соли. Если добавить 150г соли, то в растворе будет содержаться 45% соли. Найти массу соли в первоначальном растворе. [5] Решение: Пусть масса раствора -х г. Решение оформим таблицей.
Составим и решим уравнение: 0,15х + 150 = (х + 150) · 0,45 0,3х = 82,5 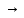 х = 275 Найдем массу чистого вещества в первоначальном растворе: 275 · 0,15 = 41,25 Ответ: 41,25г. х = 275 Найдем массу чистого вещества в первоначальном растворе: 275 · 0,15 = 41,25 Ответ: 41,25г. |
