Пояснительная записка. Проектирование машинного агрегата
 Скачать 1.28 Mb. Скачать 1.28 Mb.
|
Метрический синтез механизма насосаИз равенства (3.2) устанавливаем объем насоса: 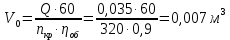 . .Рабочий ход поршня в метрах находим из равенства (3.1): 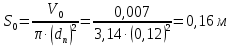 . .При соосной схеме КПМ, ход поршня определен радиусом (длиной) кривошипа: 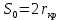 . .Таким образом искомые величины определяются следующим образом: Длина кривошипа: 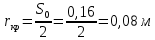 . .Длина шатуна: 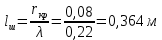 , ,где величина 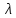 определена заданием на курсовой проект. определена заданием на курсовой проект.Результаты метрического синтеза отражаем в графической части курсового проекта. На листе формата А1 изображаем план положений механизма. Найденные длины звеньев 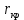 и и 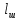 чертим в выбранном масштабе с помощью масштабного коэффициента чертим в выбранном масштабе с помощью масштабного коэффициента 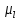 : :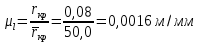 . .Размер 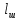 в масштабе в масштабе 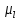 : :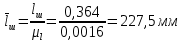 . .Кинематический анализ механизмаНа этапе кинематического анализа механизма определяются траектории, скорости и ускорения характерных точек и элементов механизма. При этом силы, действующие на механизм, не учитываются. Кинематический анализ может быть выполнен графическим и аналитическим методами. Графический методДанный метод применяется в случае, когда возникает необходимость определить скорости и ускорения характерных точек механизма и угловых скоростей и ускорений его звеньев в определенный момент времени, соответствующий определенному положению механизма. Для решения этой задачи должны быть заданы кинематическая схема механизма и закон движения начального звена (для механизмов с одной степенью свободы). График перемещений строится при определенном положении механизма за один цикл его движения. В практической работе план механизма строится для одного положения звеньев и поэтому графики их траекторий не делается. Построение планов скоростей и ускорений, основывающихся на известных теоремах теоретической механики о скоростях и ускорениях точек твердого тела, рассмотрим на примере центрального кривошипно-ползунного механизма (КПМ), схема которого в заданном положении и в соответствующем масштабе показана на рис 4.1, а. Кривошип 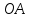 вращается с угловой скоростью вращается с угловой скоростью 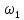 : : 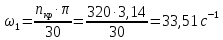 , ,Скорость точки 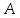 определяется как: определяется как: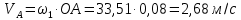 , ,и направлена перпендикулярно кривошипу 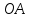 в сторону задаваемую направлением вращения. в сторону задаваемую направлением вращения.Для построения плана скоростей из произвольной точки 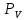 (полюса плана скоростей) в масштабе (полюса плана скоростей) в масштабе 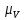 проводим вектор проводим вектор 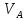 (рис 4.1, б). (рис 4.1, б).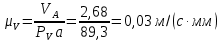 . .Скорость точки 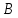 , принадлежащей как и точка , принадлежащей как и точка 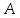 , шатуну , шатуну 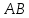 определяется по формуле: определяется по формуле: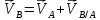 , ,где относительная скорость ( 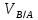 ) точки ) точки 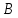 будет перпендикулярна прямой будет перпендикулярна прямой 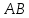 . Поэтому из конца вектора . Поэтому из конца вектора 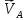 (точки (точки 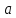 ) проводим линию перпендикулярную шатуну ) проводим линию перпендикулярную шатуну 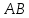 . С другой стороны, абсолютная скорость точки . С другой стороны, абсолютная скорость точки 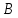 должна быть направлена по вертикали должна быть направлена по вертикали 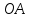 . Из полюса проводим линию параллельную линии . Из полюса проводим линию параллельную линии 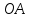 и в точке пересечения этих линий находим точку и в точке пересечения этих линий находим точку 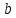 , являющуюся концом вектора абсолютной скорости точки , являющуюся концом вектора абсолютной скорости точки 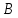 ( (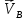 ) в выбранном масштабе плана скоростей. Вектор ) в выбранном масштабе плана скоростей. Вектор 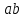 на плане скоростей соответствует относительной скорости точки на плане скоростей соответствует относительной скорости точки 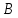 по отношению к точке по отношению к точке 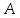 ( ( 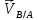 ). ).Скорость центра масс шатуна находим по теореме подобия. Отмечаем точку 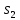 на середине отрезка на середине отрезка 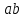 и соединяем её с полюсом. и соединяем её с полюсом.Аналогичные построения делаем для группы звеньев 4-5. Из плана скоростей находим: 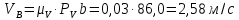 ; ;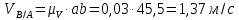 ; ;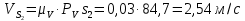 ; ;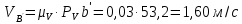 ; ;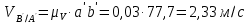 ; ;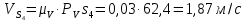 . .Угловая скорость вращения шатуна 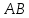 определиться как: определиться как: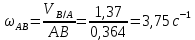 . .Угловая скорость вращения шатуна 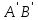 определиться как: определиться как: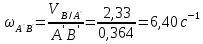 . .Для построения плана ускорений определим ускорения точки 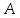 (конца кривошипа (конца кривошипа 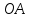 , который вращается с постоянной угловой скоростью. , который вращается с постоянной угловой скоростью.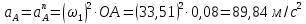 . .Это ускорение направлено из точки 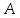 к точке к точке 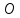 . Выбирая произвольную точку . Выбирая произвольную точку 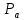 в качестве полюса плана ускорений (рис 4.1, в), переносим вектор в качестве полюса плана ускорений (рис 4.1, в), переносим вектор 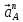 в точку полюса, в соответствующем масштабе в точку полюса, в соответствующем масштабе 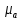 . . 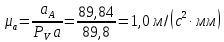 . .Ускорение точки 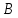 конца шатуна определится как векторная сумма ускорения точки конца шатуна определится как векторная сумма ускорения точки 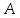 относительного центростремительного (нормального) и вращательного (тангенциального) ускорений точки относительного центростремительного (нормального) и вращательного (тангенциального) ускорений точки 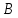 по отношению к точке по отношению к точке 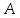 . .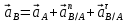 . .Направление нормального ускорения точки 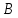 будет параллельна прямой будет параллельна прямой 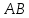 , а величина: , а величина: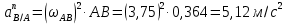 . .Размер на плане ускорений: 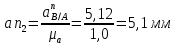 . .Строим на плане ускорений в соответствующем масштабе 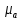 ускорение ускорение 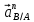 из конца вектора из конца вектора 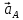 . Вращательная составляющая ускорения точки . Вращательная составляющая ускорения точки 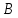 не известна по величине и направлена перпендикулярно не известна по величине и направлена перпендикулярно 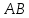 поэтому из конца вектора поэтому из конца вектора 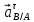 на плане ускорений проводим линию перпендикулярную на плане ускорений проводим линию перпендикулярную 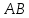 . .Абсолютное ускорение точки 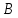 очевидно будет направлено по линии очевидно будет направлено по линии 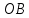 . Тогда, проводя из точки . Тогда, проводя из точки 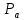 линию параллельную линию параллельную 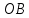 , на пересечении этих двух прямых получаем точку , на пересечении этих двух прямых получаем точку 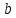 , соответствующую концу вектора , соответствующую концу вектора 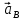 на плане ускорений. на плане ускорений. Ускорение центра масс шатуна находим по теореме подобия. Отмечаем точку 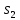 на середине отрезка на середине отрезка 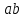 и соединяем её с полюсом. и соединяем её с полюсом.Из плана ускорений находим: 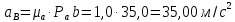 ; ;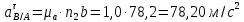 ; ;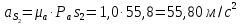 . .Найдя величину тангенциального ускорения можно определить угловое ускорение звена 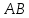 : :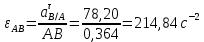 . .Из плана ускорений находим: 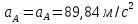 ; ; 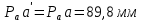 ; ;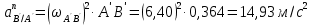 ; ;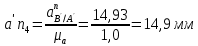 ; ;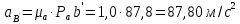 ; ;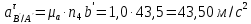 ; ;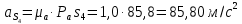 . .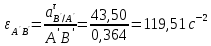 . .Графический метод исследования нагляден и универсален, так как позволяет определять скорости и ускорения звеньев механизмов любой структуры, но не обладает достаточной точностью и трудоемок. |
