Пояснительная записка. Проектирование машинного агрегата
 Скачать 1.28 Mb. Скачать 1.28 Mb.
|
Аналитический методПри решении многих практических задач, таких как расчет мощности двигателя, воздействия машины на раму и фундамент, постановка противовесов требуются выражения для перемещения, скорости и ускорения звеньев механизма. Аналитическое исследование плоских механизмов удобнее всего вести методом векторных контуров, разработанных В. А. Зиновьевым. В соответствии с этим методом нахождение кинематических характеристик механизма производится в следующем порядке: Чертим в любом промежуточном положении структурную схему механизма. Выбираем систему координат (начало обычно связывают со стойкого начального звена). Все звенья механизма, включая и стойку, заменяют векторами произвольного направления. Полученные векторы объединяют между собой так, чтобы они образовывали замкнутые контуры. В каждый контур должно входить не более двух неизвестных величин. Составляем векторные уравнения замкнутости полученных контуров в соответствии с выбранным направлением обхода. Спроектировав эти уравнения на оси координат, получим базовые системы уравнений для расчета кинематических характеристик звеньев. Обозначив, в рассматриваемом КПМ (рис 4.1), звенья механизма векторами 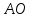 , , 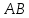 и и 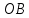 и задаваясь направлением обхода, составим уравнение замкнутости векторного контура и задаваясь направлением обхода, составим уравнение замкнутости векторного контура 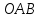 . .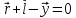 . .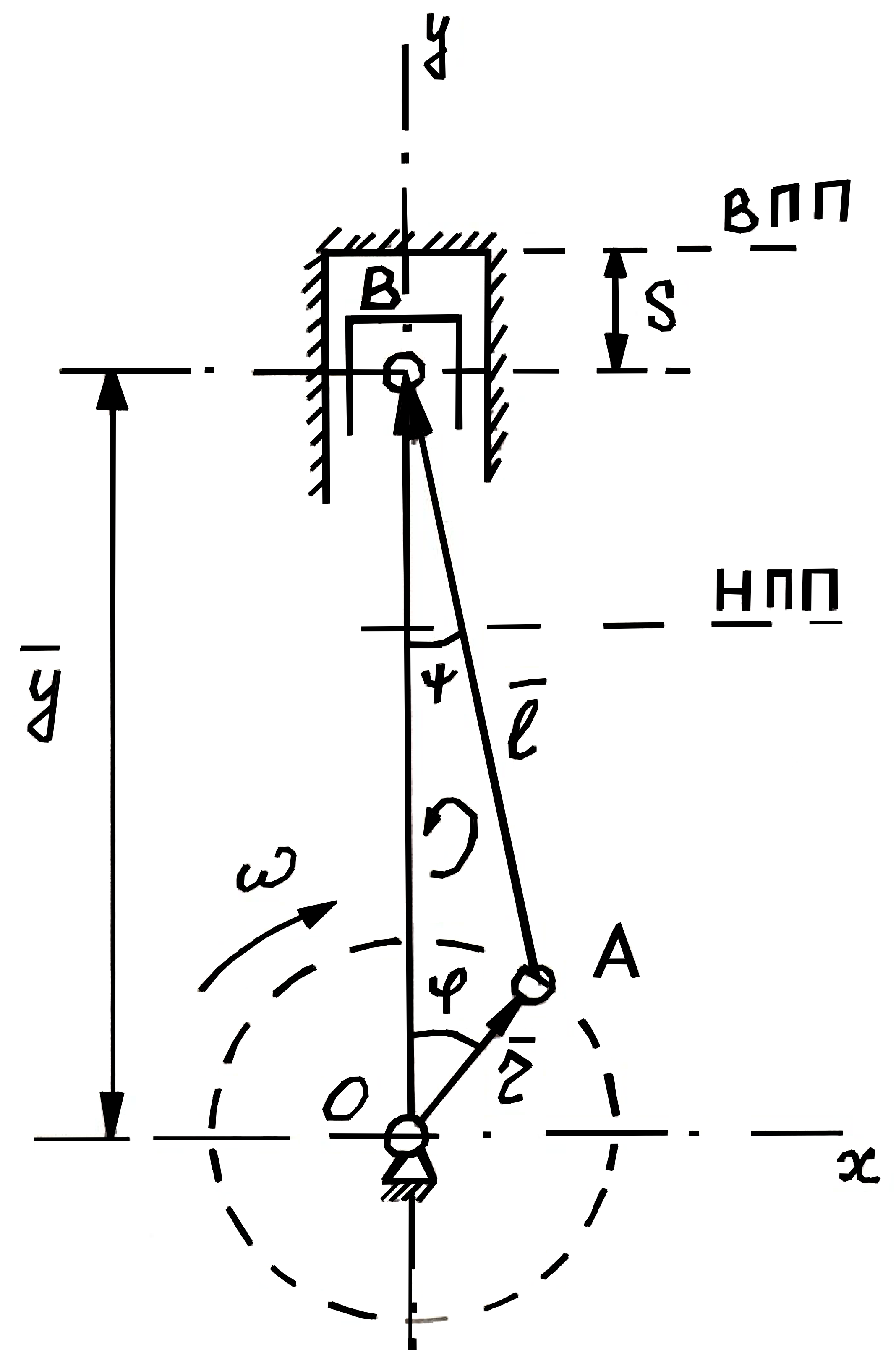 Рис. 4.1 Где 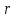 и и 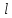 радиус кривошипа и длина шатуна соответственно. радиус кривошипа и длина шатуна соответственно.Выбрав оси координат 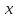 и и 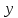 , спроектируем это уравнение: , спроектируем это уравнение: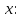 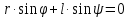 ; ;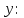 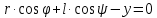 . .где неизвестными будут величина 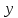 и угол и угол 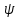 . .Решая эти уравнения получим: 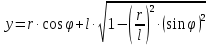 . .Откуда, учитывая, что перемещение ползуна 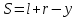 , после преобразований получим: , после преобразований получим: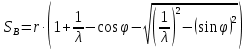 . (4.1) . (4.1)Где величина геометрического параметра будет 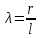 . .Скорость точки 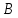 найдем беря производную по времени от выражения для перемещения (4.1): найдем беря производную по времени от выражения для перемещения (4.1):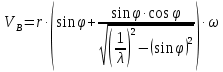 . (4.2) . (4.2)Аналогичным образом, беря производную от (4.2), можно найти выражение для ускорения точки 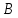 : :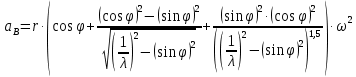 . (4.3) . (4.3)Таким образом, применение аналитических методов анализа (синтеза) плоских механизмов позволяет выводить аналитические зависимости кинематических параметров звеньев и характерных точек механизма. Аналог скорости и ускоренияКак видно из выражения (4.2) кинематические параметры ведомого звена зависят от скорости ведущего. Для удобства анализа работы механизма скорость ведомого звена удобно выражать в функции обобщенных координат ведущего звена, в качестве которых выбираются либо угол поворота 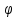 , либо перемещение , либо перемещение 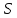 ведущего звена. Такое выражение называется аналогом скорости. ведущего звена. Такое выражение называется аналогом скорости.Так как аналог скорости зависит только от обобщенных координат и не зависят от времени кинематическое исследование механизма можно вести чисто геометрическим методом. Для рассмотренного выше примера расчета КПМ аналогами скорости ползуна, как следует из выражений (4.2), очевидно будут: 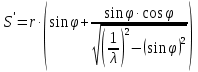 . (4.4) . (4.4)Аналог ускорения: 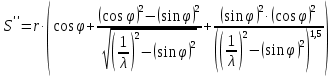 . (4.5) . (4.5)Чтобы наглядно представить характер изменения функций положения и функций аналога скорости строим их графики. |
