Проектирование редуктора вертолёта
 Скачать 0.55 Mb. Скачать 0.55 Mb.
|
3. ПРОВЕРОЧНЫЙ РАСЧЁТ ПЕРЕДАЧИ НА КОНТАКТНУЮ ПРОЧНОСТЬУсловие контактной прочности: σΗ<σΗΡ σΗ - расчётные контактные напряжения σΗΡ - допускаемое контактное напряжение (п.2.7) Расчётные контактные напряжения для цилиндрической передачи: 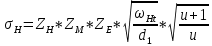 ,МПа (3.1) ,МПа (3.1)3.1Определение коэффициентов ΖΗ , ΖΜ , ΖΕ входящих в формулу для определения величины σΗ 3.1.1 Коэффициент учитывающий форму сопряжённых поверхностей зубьев ΖΗ =1,76*cosβ = 1,76 3.1.2 Коэффициент учитывающий упругие свойства материалов зубьев ZM= 270 МПа1/2 - для стальных зубьев 3.1.3 Коэффициент учитывающий суммарную длину контактных линий в зацеплении ΖΕ = 1 - для прямых зубьев 3.2 Определение удельной расчётной окружной нагрузки на зубья при расчёте контактных напряжений 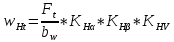 , H/мм (3.2.1) , H/мм (3.2.1)где 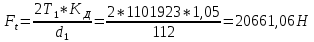 (3.2.2) (3.2.2)bw=b2=85мм - по п. 2.11 KHα=1 - по п.2.8.1 KHβ=1,09 - по п.2.8.2 Коэффициент, учитывающий дополнительную динамическую нагрузку, принятый в первом приближении равным 1, теперь определяется по формуле: 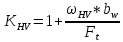 (3.2.3) (3.2.3)где ωΗV - удельная окружная динамическая нагрузка на зубья, определяемая из неравенства 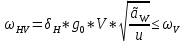 H/мм (3.2.4) H/мм (3.2.4)Где δΗ - коэффициент, учитывающий модификацию головки зуба и твердость рабочих поверхностей, выбирается из таблицы 1.9 [1] δH=0,01 - для прямых зубьев с модификацией головок при НВ>350 g0- коэффициент, учитывающий погрешность зацепления по шагу, выбирается из таблицы 1.10 [1] g0 = 53 - для степени точности при m =8 мм >3,55 мм ωV - предельное значение удельной окружной динамической силы , выбирается из таблицы 1.10 [1] ωV = 310 H / мм - для степени точности при m =8 мм >3,55 мм 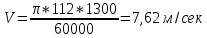 После подстановки числовых значений в формулу (3.2.4) 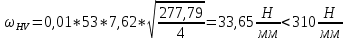 Так как неравенство выполняется, окончательное значение удельной окружной динамической нагрузки на зубья: ωΗV= 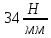 После подстановки числовых значений в формулы (3.2.3) и (3.2.1) 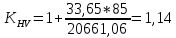 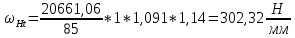 3.3 Определение расчётных контактных напряжений 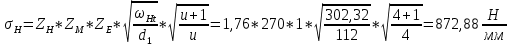 3.4 Проверка контактной прочности зубьев передачи σH≤σHP 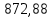 МПа< МПа<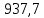 МПа МПагде σΗΡ= 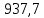 МПа - по п.2.7 МПа - по п.2.7Условие прочности выполняется 4.ПРОВЕРОЧНЫЙ РАСЧЁТ ПЕРЕДАЧИ НА ИЗГИБНУЮ ПРОЧНОСТЬУсловие изгибной прочности для зубьев шестерни и колеса: σF1< σFΡ1 и σF2< σFΡ2 σΡΧ 2 - расчётное местное изгибное напряжение на переходной поверхности у основания зуба со стороны растяжения σF1, 2 - допускаемое изгибное напряжение 4.1 Определение расчётного местного напряжения у основания зуба шестерни и колеса σF1,2 Для цилиндрической передачи: 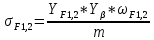 (4.1) (4.1)4.1.1 Коэффициент, учитывающий форму профиля зуба для колёс с наружными зубьями YF1,2= 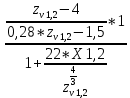 (4.1.1) (4.1.1)
x1=+0,3 x2=-0,3 x1 и x2-коэффициенты смещения инструмента После подстановки числовых значений YF1= 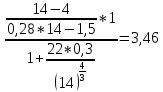 YF2= 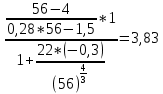 4.1.2 Коэффициент, учитывающий наклон линии зуба Υβ= 1 - для прямых зубьев 4.1.3 Определение удельной расчётной окружной нагрузки на зубья при расчёте на изгиб 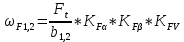 , (4.1.2) , (4.1.2)где 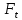 = =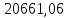 Н - по п.3.2 Н - по п.3.2b1,2 - действительная ширина зубчатого венца шестерни или колеса b1=105мм, b2 = 85мм - по п.2.11 Коэффициент, учитывающий распределение нагрузки между зубьями при расчёте на изгиб 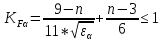 (4.1.3) (4.1.3)где n - степень точности зацепления n =8 εα- коэффициент торцевого перекрытия зубьев εα1и εα2- частные коэффициенты перекрытия , выбираемые согласно рекомендациям п.2.8.4 с помощью графика рис.1.6 εα=εα1(1+x1)+ εα2(1+x2)= 0,77*(1+0.3)+0,86*(1-0,3)=1,6(4.1.4) После подстановки числовых значений в формулу (4.1.3) KFa= 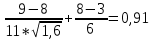 Так как неравенство выполняется, принимаем КFа =0,91 ΚFβ- коэффициент, учитывающий неравномерность распределения нагрузки по длине зуба ΚFβ= ΚΗβ= 1,09 ( по п.2.8.2 ), т.к. значения коэффициента одинаковы при расчёте на зубья 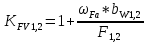 (4.1.5) (4.1.5)где bW1,2 - рабочая ширина венца шестерни и колеса 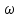 FV- удельная окружная динамическая нагрузка на зубья, определяемая изнеравенства: FV- удельная окружная динамическая нагрузка на зубья, определяемая изнеравенства: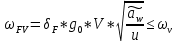 (4.1.6) (4.1.6)где δF- коэффициент, учитывающий модификацию головки зуба и твердость рабочих поверхностей, выбирается из таблицы 1.9 [1] δΗ= 0,010 - для прямых зубьев с модификацией головок по п.5.1.3 [1] g0- коэффициент, учитывающий погрешность зацепления по шагу, выбирается изтаблицы 1.16 [1] g0 = 61 - для 8 степени точности при m = 2,5мм< 3,55 мм; 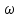 V —предельное значение удельной окружной динамической силы , выбираетсяиз таблицы 1.16 [1] V —предельное значение удельной окружной динамической силы , выбираетсяиз таблицы 1.16 [1]ων= 410 Н/ мм - для 8 степени точности при m= 8мм> 3,55 мм После подстановки числовых значений в формулу (4.1.6) 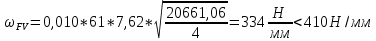 Так как неравенство выполняется, окончательное значение удельной окружной динамической нагрузки на зубья ωFν=  Н / мм Н / ммТогда коэффициент, учитывающий дополнительную динамическую нагрузку на зубья: 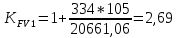 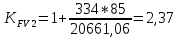 В результате после подстановки удельная расчётная окружная нагрузка на зубья шестерни и колеса при расчёте на изгиб:  F1 = F1 =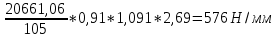 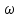 F2 = F2 =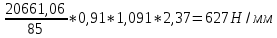 4.1.4 Расчётные местные напряжения изгиба у основания зубьев шестерни и колеса σF1 = ΥF1* Υβ* 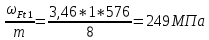 σF2 = ΥF2* Υβ* 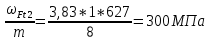 4 (4.2.1) .2 Определение допускаемых напряжений изгиба в расчётных точках зубьев шестерни и колеса, работающих в условиях частого реверсирования 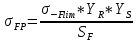 4.2.1 Определение предельных напряжений изгиба при двухстороннем приложении нагрузки в зубьях шестерни и колеса Предельные напряжения изгиба σFlim при одностороннем приложении нагрузки зависят от числа циклов напряжений и для стальных зубьев определяются из неравенства: 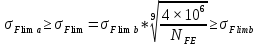 (4.2.2) Для стальных зубьев при НВ> 350 верхний и нижний пределы выбираются согласно рекомендациям табл. 1.17: Для шестерни σFlima= 1600 МПа σFlimb= 950 МПа Для колеса σFlima= 20НRС+500 = 20  53+500=1560МПа 53+500=1560МПаσFlimb=12НRС+300 = 12  53+300=936МПа 53+300=936МПаРасчётное число циклов изменения напряжений изгиба: NFE=60  c c n n NЦН (4.2.3) NЦН (4.2.3)Число зацеплений за один оборот с =1 По исходным данным число циклов нагружения передачи NЦН= 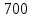 циклов. циклов.Частота вращения шестерни n1 = 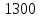 об / мин об / минЧастота вращения колеса n2 = 330об / мин После подстановки числовых значений в формулу (4.2.3) NFE1=tFE  c c n1 n1 NЦН=60 NЦН=60 1 1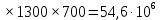 NFE2=tFE  c c n2 n2 NЦН=60 NЦН=60 1 1 330 330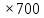 = =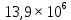 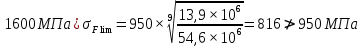 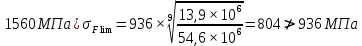 Так как неравенства не выполняются принимаем: σFlim1 = 950 МПа σFlim2 = 936 МПа Предельные напряжения изгиба для двухстороннего приложения нагрузки: σ (4.2.4) -F lim = σF lim  (1-γFC (1-γFC δF δF δN) δN)где согласно рекомендациям п.5.2.1 [1]: γFC =0,25 - коэффициент, определяющий относительное снижение предела выносливостиприR= -1 при НВ > 450 δΡ- коэффициент, учитывающий несимметричность знакопеременной циклограммы нагружения; при одинаковой величине нагрузки по положительной и отрицательной сторонам циклограммы δF =1 δN- коэффициент, учитывающий соотношение эквивалентных чисел циклов изменения изгибного напряжения по положительной и отрицательной сторонам циклограммы; при одинаковом времени работы по обеим сторонам циклограммы δΝ= 1 После подстановки числовых значений σ-Flim1= 950  (1-0,25 (1-0,25 1 1 1)=712,5 МПа 1)=712,5 МПаσ-Flim2= 936  ( 1-0,25 ( 1-0,25 1 1 1)=702 МПа 1)=702 МПа4.2.2 Коэффициент, учитывающий влияние шероховатости переходной поверхности у основания зуба на изгибную прочность YR1=YR2=1,05 – при шлифованных поверхностях НВ>350 4.2.3 Коэффициент, учитывающий чувствительность материала зубьев к концентрации напряжений и масштабный эффект 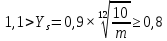 (4.2.5) (4.2.5)После подстановки числовых значений 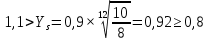 Так как неравенства выполняются, принимаем: Ys=0,92 4.2.4 Коэффициент безопасности при расчёте зубьев на изгиб Величина SF зависит от требуемой вероятности безотказной работы. Вероятность безотказной работы зубчатой пары Р>0, SF=2,2 -в соответствии с назначением механизма и рекомендациями п.5.2.4 4.2.5 Допускаемые напряжения изгиба в расчётных точках зубьев шестерни и колеса 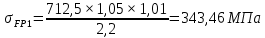 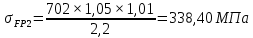 4.3 Проверка изгибной прочности зубьев шестерни и колеса 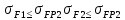 Для шестерни: Для колеса: 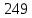 МПа< МПа<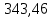 МПа МПа 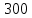 МПа< МПа<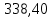 МПа МПаУсловия прочности выполняются, зубья шестерни и колеса прочны при действии напряжений изгиба. |
