Проектирование редуктора вертолёта
 Скачать 0.55 Mb. Скачать 0.55 Mb.
|
2. ПРОЕКТИРОВОЧНЫЙ РАСЧЕТ МЕХАНИЗМА2.1 Выбор материала зубчатой передачи Исходя из прототипа выбирается марка стали для шестерни и зубчатого колеса. Материал для шестерни:сталь 18Х2Н4ВА ГОСТ 4543-71 НВ = 580 σΒ= 1030 МПа σТ=785МПа σ-1= 570 МПа ТХО - азотирование после термоулучшения Материал для зубчатого колеса: сталь 40ХН2МА ГОСТ 4543-71 ТХО - азотирование после термоулучшения. НВ = 530 σВ=980МПа σТ= 835 МПа σ-1= 550Мпа 2.2. Определение чисел зубьев шестерни z1, колеса z2 и передаточного числа Ориентировочное значение окружной скорости 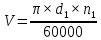 , м/сек (2.2.1) , м/сек (2.2.1)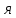 Где d1=60мм -делительный диаметр шестерни прототипа (исходные данные) n1 –частота вращения шестерни 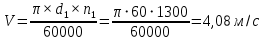 Суммарное число зубьев zΣ имеет характерные значения для зубчатых пар различных категорий. Суммарное число зубьев xΣ =50…60(70 ) xΣ =70 Тогда число зубьев шестерни в первом приближении: 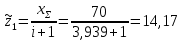 (2.2.2) (2.2.2)Где i – передаточное отношение передачи 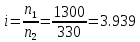 (2.2.3) (2.2.3)Где n2 –частота вращения колеса Число зубьев колеса в первом приближении: 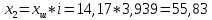 (2.2.4) (2.2.4)Принимаем: z1=14 z2=56 Передаточное число для принятых зубьев: 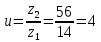 (2.2.5) (2.2.5)Отклонение передаточного числа: 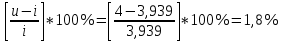 (2.2.6) (2.2.6)Отклонение меньше 2,5% и не должно превышать передаточное число 4,5 Принимаем за передаточное число значение u = 4 Так как z1 =14, то для устранения подрезания зубьев шестерни вводят корригирование. Зацепления с коэффициентами смещения инструмента x1 =+0,3 х2=-0,3 х1 и х2 - коэффициенты смещения инструмента 2.3 Выбор степени точности зацепления При частоте вращения шестерни n1 = 1300об / мин, с учётом размеров зубчатых колёс прототипа, ожидается окружная скорость V= 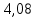 м/с. Поэтому с учётом степени надёжности механизма и реверсивного движения принимается 7 степень точности и вид сопряжения - С. м/с. Поэтому с учётом степени надёжности механизма и реверсивного движения принимается 7 степень точности и вид сопряжения - С.2.4 Выбор относительной ширины зубчатого венца В соответствии с рекомендациями и по табл. 1.2[1] для цилиндрических передач выбирается ψba=0,3 2.5 Выбор формы выполнения зуба Так как полученная окружная скорость шестерни менее20 м/с , то выбирается прямая форма зуба (β=0). 2.6 Определение предельных контактных напряжений в зубьях шестерни и колеса Предельные контактные напряжения зависят от твёрдости поверхности зубьев и числа циклов нагружения поверхности детали σH lim min=min(σH lim 1,σH lim 2) Предельное контактное напряжение для поверхности зуба шестерни определяется по формуле: 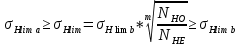 (2.6.1) (2.6.1)Где σHlimaи σHlimb- соответственно верхнее и нижнее значения предельных напряжений, которые выбираются по таблице 1.6 [1] m=6 - так как шестерня и колесо из стали NHO - число циклов изменении напряжении, соответствующих излому кривой усталости, для стали 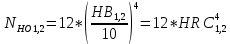 (2.6.2) (2.6.2)NHE - расчетное число циклов изменения контактных напряжений на одной поверхности зубьев Расчётное число циклов изменения контактных напряжений на одной поверхности зуба шестерни: NHE1=60*c *n1* 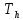 (2.6.3) (2.6.3)Принимаем эквивалентную длительность цикла нагружения одной поверхности равной длительности одностороннего вращения в течении одного цикла по циклограмме Th =700 ч -расчётная долговечность с = 1 - число контактов одной поверхности зуба шестерни за один оборот. Для стальных зубьев верхний и нижний пределы вычисляются согласно таблице 1.6 [1]. σH lim a1=42*HRC, МПа (2.6.5) σH lim b1=23*HRC, МПа (2.6.6) 1)Для шестерни HRC=58 по формуле (2.6.5)σHlima1= 42*58=2436 МПа по формуле (2.6.6)σHlimb1=23*58=1334 МПа по формуле (2.6.2) NHO=12* 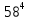 =135,8* =135,8*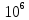 по формуле (2.6.3) NHE1=60*1* 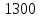 *700=54,6* *700=54,6*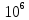 Предельное контактное напряжение для поверхности зуба шестерни σHlim 1= 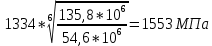 2436 МПа> 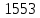 МПа> 1334 МПа МПа> 1334 МПаТак как неравенство выполняется, принимаем: σHlim 1= 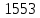 МПа МПа2) Для колеса HRC=53 σH lim a2=42*53=2226МПа σH lim b2=23*53=1219МПа По формуле (2.6.2) NHO2=12* 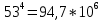 По формуле (2.6.3) NHE2=60*1*330*700 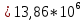 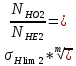 1219* 1219*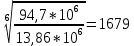 МПа МПа2226 МПа> 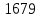 MПа> 1219 Мпа MПа> 1219 МпаНеравенство выполняется, принимаем: σHlim 2= 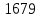 МПа МПаСравниваются значения σΗ lim1, и σΗ lim2 и минимальное из них принимаем в качестве σH lim min=min(σΗ lim1, σΗ lim2)= 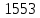 МПа МПа2.7 Определение допускаемой величины контактных напряжений в зубьях передачи Допускаемое контактное напряжение: 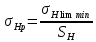 (2.7.1) (2.7.1)где SH=1,3 -коэффициент безопасности по таблице 1.7 [1] соответствующий назначению механизма при вероятности безотказной работы зубчатой пары Р > 0,99 Подставляя числовые значения в формулу (2.7.1), получаем: 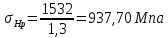 2.8 Определение значений коэффициентов КНα, ΚΗβ , ΚΗV и функции ƒ(β), входящих в формулу определения межосевого расстояния 2.8.1 Коэффициент, учитывающий распределение нагрузки между зубьями при расчёте на контактную выносливость KHα=1 – для прямозубых пар 2.8.2 Коэффициент, учитывающий неравномерность распределения нагрузки по ширине зубчатых венцов 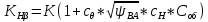 (2.8.1) (2.8.1)где К - коэффициент неравномерности К = 1 - для прямозубых пар cH- коэффициент, учитывающий относительную твёрдость контактных поверхностей 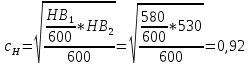 (2.8.2) (2.8.2)Ψba=0,3 - по п.2.4 сθ- коэффициент, учитывающий влияние деформации скручивания шестерни и углов прогиба валов сθ=0,2 - согласно заданной кинематической схеме рис. 1.3 [1] Cоб - коэффициент, учитывающий влияние смягчения краев обода колеса Соб=0,9 - принимая обод колеса податливым рис. 1.4[1] После подстановки числовых значений в формулу (2.8.1): 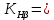 1*(1+0,2* 1*(1+0,2*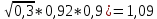 1 12.8.3 Коэффициент, учитывающий дополнительную нагрузку В первом приближении: ΚΗV = 1 2.8.4 Функция ƒ(β) ƒ(β) = 1- при прямых зубьях 2.9 Определение межосевого расстояния цилиндрической зубчатой передачи в первом приближении  , мм (2.9.1) , мм (2.9.1)где T1 - номинальный вращательный момент на ведущем звене передачи (шестерне), Н*мм 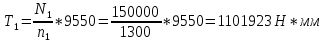 (2.9.2) (2.9.2)Кд - коэффициент динамичности Кд = 1,05 (исходные данные) Епр - приведённый модуль упругости материала шестерни и колеса, МПа Для стали Eпр=E1=E2=2.1*105 МПа KHα=1 - коэффициент, учитывающий распределение нагрузки между зубьями После подстановки числовых значений в (2.9.1): 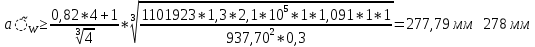 2.10 Определение модуля зацепления в первом приближении 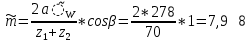 (2.10.1) (2.10.1)Из табл. 1.7[1] выбираем стандартное значение модуля m = 8 2.11 Определение основных размеров зубчатой передачи Диаметры делительных и начальных окружностей ( d и dw ) при коррегировании с коэффициентами смещения х1 + х2 = 0 совпадают, т.е. 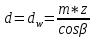 (2.11.1) (2.11.1)Тогда для шестерни и колеса: 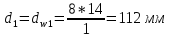 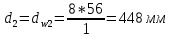 Диаметры окружностей вершины зубьев: da=d+2m+2xm (2.11.2) da1=112+2*8+2*0,3*8=132,8 мм da2=448+2*8-2*0,3*8=459,2 мм Диаметры окружностей впадин зубьев: dƒ=d-2.5m+2xm(2.11.3) dƒ1=112-2,5*8+2*0,3*8=96,8мм dƒ2=448-2,5*8-2*0,3*8=423,2мм Межосевое расстояние (окончательная величина): 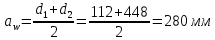 Примем за 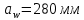 (2.11.4) (2.11.4)Рабочая ширина венца в первом приближении: b̃w=ψba*ãw=0,3*277,79=83,337мм (2.11.5) Действительную ширину зубчатого венца получаем округлением в сторону увеличения до нормального линейного размера по табл. 1.12 [1]: b1=105мм b2=85мм Тогда окончательная величина рабочей ширины зубчатого венца (определяющая область действия контактных напряжений): bw=min(b1,b2)=85мм |
