Жолдыбалина Н. (7-8). Программа курса подготовка к олимпиаде по математике

Название	Программа курса подготовка к олимпиаде по математике
Дата	11.04.2023
Размер	90.98 Kb.
Формат файла
Имя файла	Жолдыбалина Н. (7-8).docx
Тип	Программа курса #1054768

«Бекітемін»

Астана қаласы Қадыр Мырза Әлі

атындағы BINOM SCHOOL

мектеп-лицейінің директоры

_________________А.Д.Макышева

«____»___________2023ж

ПРОГРАММА КУРСА

«ПОДГОТОВКА К ОЛИМПИАДЕ ПО МАТЕМАТИКЕ»

7-8 КЛАСС

38 ЧАСОВ

Подготовила учитель математики:

Жолдыбалина Н.Т

Астана 2023
Пояснительная записка
Программа курса «Подготовка к олимпиаде по математике» для учащихся 7-8 классов, имеет естественнонаучную направленность и рассчитана на 38 часов.

Данная программа представляет собой дополнительный этап обучения математике на профильном уровне для учащихся среднего и старшего школьного возраста. Она основана на комплекте программ, объединенных общей целью - овладеть основами математического мышления и математического аппарата путем решения нестандартных задач олимпиадного уровня. Программа также знакомит студентов с незнакомыми теоретическими материалами в области комбинаторики, графов, четности, инвариантов, неравенств, делимости, сравнений по модулю и других направлениях.
Цель этого курса заключается в обучении учащихся анализу и решению сложных математических задач, которые являются нестандартными и используются на олимпиадах, путем формирования математического мышления и развития интеллектуальной активности. Этот курс способен удовлетворить потребности обучающихся, которые заинтересованы в более глубоком изучении математики, и предоставляет возможность каждому ученику проявить свои способности. Курс построен как повторение и углубление тем, которые изучаются в основной программе математики в школе, и проводится в рамках внеурочной деятельности. Углубление материала достигается путем обучения методам и приемам решения математических задач, которые требуют высокой логической и операционной культуры и развивают научно-теоретическое мышление учащихся. Занятия дают возможность ученикам более полно изучить программный материал, решить задачи повышенной сложности и развить свои творческие способности, не ограничивая уровень сложности задачного материала заранее. Этот курс также поможет повысить уровень математической подготовки учащихся.
Практическая значимость:

Курс алгебры 7-8 классов, который входит в программу школьного образования, имеет высокую практическую значимость в нашем современном обществе. В процессе изучения курса учащиеся развивают абстрактное мышление, логическое и алгоритмическое мышление, а также такие качества мышления, как сила и гибкость, конструктивность и критичность. Курс также способствует формированию математического стиля мышления, который включает различные методы, такие как индукция, дедукция, анализ, синтез, классификация, систематизация, абстрагирование и аналогия. Особое внимание уделяется мотивации и объяснению основных понятий, методов и идей, а также демонстрации возможностей их применения на практике. Курс построен на теории развивающего обучения и включает упражнения, направленные на сравнение, анализ, выделение главного, установление связей, классификацию, обобщение и систематизацию.

Курс внеурочной деятельности по данной программе составляет 38 учебных часов в год, с проведением занятий по 1 часу в неделю. Он является Изучение данного курса способствует- развитию личностных, метапредметных и предметных результатов обучения, соответствующих требованиям ГОСО РК.
Программа направлена на:

развитие ответственного отношения у учащихся к учению, их готовности и способности к саморазвитию и самообразованию на основе мотивации к обучению и познанию;
формирование осознанного выбора и построения дальнейшей индивидуальной траектории образования на базе ориентировки в мире профессий и профессиональных предпочтений с учетом устойчивых познавательных интересов, а также на основе формирования уважительного отношения к труду, развитие опыта участия в социально значимом труде;
развитие критичного мышления, инициативы, находчивости и активности при решении математических задач.

Кроме того, программа направлена на развитие у учащихся метапредметных результатов, таких как:

умение самостоятельно определять цели своего обучения, ставить и формулировать для себя новые задачи в учебе, развивать мотивы и интересы своей познавательной деятельности;
осуществлять контроль своей деятельности в процессе достижения результата, определять способы действий в рамках предложенных условий и требований, корректировать свои действия в соответствии с изменяющейся ситуацией;
развитие компетентности в области использования информационно-коммуникационных технологий;
формирование первоначальных представлений об идеях и методах математики как об универсальном языке науки и техники, а также как средстве моделирования явлений и процессов.

Предметные результаты обучения по данному курсу включают:

Развитие математических знаний и навыков, необходимых для решения олимпиадных и нестандартных задач, таких как анализ и синтез информации, обобщение, классификация, алгоритмизация, логическое и аналитическое мышление, решение задач на соответствие, нахождение закономерностей и зависимостей, создание и анализ математических моделей и т.д.
Формирование умения применять математические знания и навыки на практике в реальных жизненных ситуациях, включая решение задач в различных областях знания, таких как физика, химия, биология, экономика и т.д.

Развитие умения работать в коллективе, обмениваться знаниями и опытом с другими учениками, а также умения самостоятельно и эффективно работать над математическими задачами.
Подготовка учеников к участию в олимпиадах по математике и других научных конкурсах, а также к продолжению обучения в профильных классах в старших классах.

В целом, данная программа по Месту курса внеурочной деятельности в учебном плане направлена на развитие учеников в широком спектре компетенций, включая не только математические знания и навыки, но и личностные и метапредметные результаты обучения.

Критерии оценивания данного курса:

В рамках данной образовательной программы оцениваются планируемые результаты курса, которые включают подготовку школьников к участию в различных математических мероприятиях, таких как конференции, олимпиады и турниры. В процессе обучения ученики развивают навыки работы с научной литературой, узнают о новых областях математики и учатся применять свои знания в смежных областях. В конце курса они приобретают навыки логического мышления, умение работать в команде и знания в теории остатков, сравнений и методах математической индукции. Они также развивают навыки математической аргументации и стройности суждений, которые могут быть применены в различных областях жизни. Результаты обучения оцениваются на итоговой олимпиаде и на других мероприятиях на различных уровнях.

Алгебра - это раздел математики, который изучает операции с числами, переменными, функциями и многочленами. В подготовке к олимпиаде важно уделить внимание алгебраическим формулам и уравнениям, работе с функциями, а также графическому представлению алгебраических зависимостей.

Геометрия - это раздел математики, который изучает пространственные формы, их свойства и взаимоотношения. В подготовке к олимпиаде важно уделить внимание геометрическим фигурам, теоремам, связанным с углами, длинами и площадями, а также геометрическим преобразованиям и пространственной геометрии.

Теория чисел - это раздел математики, который изучает свойства чисел и их взаимоотношения. В подготовке к олимпиаде важно уделить внимание теоремам, связанным с делением, наибольшим общим делителем, наименьшим общим кратным и простыми числами.

Комбинаторика - это раздел математики, который изучает методы подсчета и анализа комбинаций и перестановок объектов. В подготовке к олимпиаде важно уделить внимание задачам на подсчет различных комбинаций, задачам на перестановки и сочетания, а также задачам на графы и деревья.

Содержание курса

Раздел 1. Алгебра. (10 часов)

1.1 Диофантовы уравнения - это уравнения, в которых необходимо найти целочисленные решения. Они названы в честь античного математика Диофанта Александрийского, который занимался изучением этого типа уравнений. Обычно диофантовы уравнения связаны с теорией чисел и алгеброй.

Примеры диофантовых уравнений для 7 класса могут включать уравнения вида:

x + y = 7, где x и y - целые числа

2x + 3y = 14, где x и y - целые числа

х² + y² = 25, где x и y - целые числа

x³ + y³ = 728, где x и y - целые числа

Решение диофантовых уравнений может быть достаточно сложным, но для подготовки к олимпиаде важно знать, как работать с целыми числами и решать простые диофантовы уравнения.

1.2 Уравнения с модулем - это уравнения, содержащие модуль (абсолютную величину) переменной. Пример: |x-3| + |x+2| = 5.

1.3 Уравнения с параметрами - это уравнения, которые содержат один или несколько параметров, которые могут быть произвольными числами.

Пример: x² + (a+b)x + ab = 0.

1.4 Уравнения в целых и натуральных числах относятся к разделу алгебры и изучаются на математических олимпиадах различного уровня. Одним из ключевых понятий в этом разделе является метод остатков, который позволяет решать различные задачи, связанные с целыми числами. Кроме того, при подготовке к олимпиаде необходимо уметь составлять уравнения в числовых задачах, которые могут включать в себя такие понятия, как проценты, доли, пропорции и другие. Важно не только уметь решать уравнения, но и анализировать их свойства и особенности, например, наличие или отсутствие целочисленных решений.

Раздел 2. Геометрия. (10 часов)

2.1 Задачи на построение с помощью циркуля и линейки.

Круг задач, рассматриваемых в геометрии, очень широк. Среди них особое место занимают задачи на построение, которые способствуют развитию определенности, последовательности и обоснованности мышления. На этих задачах можно научиться таким методам познания, как анализ и синтез.

Структура решения задачи на построение.

Решение задач на построение с помощью циркуля и линейки, состоит не в том, чтобы выполнить соответствующие построения, а в том, чтобы найти алгоритм решения, то есть, описать решение задачи в виде последовательности уже известных стандартных построений. Правильное, осмысленное решение задач на построение состоит из основных этапов: анализ, построение, доказательство (синтез), исследование.

Анализ. Составляется план решения. Для этого поступают так: предполагают задачу решенной, делают от руки примерный чертеж искомой. Нужно найти такую зависимость между данными и искомыми величинами, которая позволила бы определить положение искомой точки (отрезка или угла), на нахождение которых нацелено решение задачи.

Построение – механическое выполнение тех приемов, которые были выведены из плана решения задачи, т.е. анализа. При построении используют основные приемы (задачи на построение), т.е. любая задача на построение разбивается на конечное число шагов (простейших задач на построение).

Доказательство. Когда искомая фигура построена, необходимо доказать, что она удовлетворяет всем требованиям задачи. При этом ход рассуждений будет обратный тому, который применялся при анализе. Поэтому иногда доказательство называют синтезом.

Исследование имеет целью выяснить, всегда ли задача разрешима, сколько решений допускается (одно или несколько). Необходимо рассмотреть всевозможные частные случаи, причем нужно выяснить, меняется ли ход решения в них и как именно.
Основные построения с помощью циркуля и линейки.

Для выполнения основных построений с помощью циркуля и линейки используется метод решения, при котором искомую точку строят как точку пересечения множеств (геометрических мест), определяемых некоторыми условиями. Данный метод так и называется – метод пересечения множеств или метод геометрических мест. С помощью этих инструментов мы можем выполнить огромное множество построений. Какие простейшие построения являются стандартными? Авторы учебников [1], [6] к основным построениям в 7 классе относят:

построить отрезок, равный данному отрезку; построить середину отрезка.
построить перпендикуляр к прямой, построить серединный перпендикуляр.
построить угол, равный данному углу; построить биссектрису угла.
построить треугольник (по трём сторонам, по двум сторонам и углу между ними, по стороне и двум прилежащим к ней углам, по двум сторонам и углу, противолежащему одной из сторон).
построить прямоугольный треугольник (по гипотенузе и катету, по гипотенузе и острому углу).
построить прямую, проходящую через данную точку параллельно данной прямой.

Раздел 3. Теория чисел. (8 часов)

Олимпиадные задачи «Теория чисел»

Задача 1. Петин счет в банке содержит 500 долларов. Банк разрешает совершать операции только двух видов: снимать 300 долларов или добавлять 198 долларов.
Какую максимальную сумму Петя может снять со счета, если других денег у него нет?

Задача 2. Наибольший общий делитель (НОД) натуральных чисел m и n равен 1. Каково наибольшее возможное значение НОД чисел m+2000n и n+2000m?

Задача 3. Докажите, что произведение любых трёх последовательных натуральных чисел делится на 6.

Задача 4. Найдите все натуральные n > 1, для которых n³ – 3 делится на n – 1.

Задача 5. Докажите, что любое натуральное число, десятичная запись которого состоит из 3-х одинаковых цифр, делится на 37.

Задача 6^*. Сумма трёх различных наименьших делителей некоторого числа A равна 8. На сколько нулей может оканчиваться число A?

Задача 7^*. Докажите, что число, имеющее нечётное число делителей, является точным квадратом.

Задача 8 ^*.Найдите наименьшее натуральное n, для которого

(n + 1)(n + 2)(n + 3)(n + 4) делится на 1000.

Задача 9^*. Даны числа: 4, 14, 24, ..., 94, 104. Докажите, что из них нельзя вычеркнуть сперва одно число, затем из оставшихся ещё два, затем ещё три и, наконец, ещё четыре числа так, чтобы после каждого вычёркивания сумма оставшихся чисел делилась на 11.

Задача 10^*. Докажите, что все числа 10017, 100117, 1001117, ... делятся на 53.

Задача 11^*. Доказать, что 7 + 7² + ... + 7⁴^K, где K - любое натуральное число, делится на 400.

Задача 12^* Найдите все такие числа a, что для любого натурального n число an(n + 2)(n + 3)(n + 4) будет целым.

Задача 13^* Назовём натуральное число хорошим, если среди его делителей есть ровно два простых числа.
Могут ли 18 подряд идущих натуральных чисел быть хорошими?

Задача 14^*. Доказать, что 1¹⁹⁸³ + 2¹⁹⁸³ + ... + 1983¹⁹⁸³ делится на 1 + ... + 1983.

Задача 15^*. Сумма кубов трёх последовательных натуральных чисел оказалась кубом натурального числа. Докажите, что среднее из этих трёх чисел делится на 4.
Решения к задачам

Решение задачи 1: Поскольку 300 и 198 делятся на 6, Петя сможет снять лишь сумму, кратную 6 долларам. Максимальное число, кратное 6 и не превосходящее 500, - это 498.

Докажем, что снять 498 долларов возможно. Произведем следующие операции: 500-300=200, 200+198=398, 398-300=98, 98+198=296, 296+198=494. Сумма, лежащая в банке, уменьшилась на 6 долларов.

Проделав аналогичную процедуру 16 раз, Петя снимет 96 долларов. Затем он может снять 300, положить 198 и снова снять 300. В результате у него будет 498 долларов.

Решение задачи 2: Пусть a=2000m+n, b=2000n+m, d - наибольший общий делитель a и b. Тогда d делит также числа

2000a-b=(2000²-1)m и 2000b-a=(2000²-1)n.

Поскольку m и n взаимно просты, то d делит 2000²-1. С другой стороны, при m=2000²-2000-1, n=1, получаем a=(2000²-1)(2000-1), b=2000²-1=d.

Ответ: 2000²-1.

Решение задачи 3: Среди этих трёх чисел есть хотя бы одно чётное число. Значит, в разложении произведения на простые множители есть множитель 2.
Среди этих трёх чисел одно число делится на 3. Значит, в разложении произведения на простые множители есть множитель 3.
В разложении произведения на простые множители есть простые числа 2 и 3. Значит, оно делится на их произведение, то есть на 6.

Решение задачи 4 : n3 – 3 = (n3 – 1) – 2. Первое слагаемое делится на n – 1, значит, и 2 делится на n – 1. Следовательно, n – 1 = 1 или , n – 1=2.

Ответ: n = 2, 3.

Решение задачи 5: Такое число делится на 111 = 3·37.

Решение задачи 6*: Число 8 можно представить в виде суммы трёх различных натуральных чисел двумя способами: 8 = 1 + 2 + 5 = 1 + 3 + 4. Числа 1, 3 и 4 не могут быть тремя наименьшими делителями числа A: если A делится на 4, то оно делится и на 2. Значит, три наименьших делителя A – это 1, 2 и 5. Таким образом, A делится на 10, но не делится на 4. Следовательно, число A оканчивается ровно на один нуль.
Ответ: На один нуль.

Решение задачи 7*: Если d – делитель числа n, то n/d – также делитель. Таким образом, все делители числа делятся на пары. Если число имеет нечётное число делителей, то делители какой-то пары совпадают. Тогда d = n/d, откуда n = d 2, то есть число n – квадрат целого числа.

Решение задачи 8 *: При любом натуральном n данное произведение делится на 8, так как среди любых четырёх последовательных натуральных чисел одно делится на 4 и еще одно – на 2. Следовательно, достаточно найти наименьшее n, для которого данное произведение делится на 125 = 53. Так как на 5 может делиться только один из множителей, то n – наименьшее, если множитель, делящийся на 125, – наибольший. Значит, n + 4 = 125, то есть n = 121.

Ответ: n = 121.

Решение задачи 9*: Всего дано 11 чисел, а нужно вычеркнуть 10 чисел. Поэтому в конце должно остаться одно число, кратное 11, то есть число 44. С другой стороны, число 44 мы должны вычеркнуть самым первым. Действительно, сумма всех данных чисел равна 11·108 : 2, поэтому она делится на 11. Следовательно, если после вычёркивания одного числа сумма оставшихся чисел делится на 11, то вычеркнутое число тоже делится на 11.

Решение задачи10*: Умножив такое число на 9, получим число 9010...053, которое делится на 53, так как 901 = 53·17. Значит, и исходное число делится на 53.

Решение задачи11*: Данную сумму можно сгруппировать следующим образом:
(7 + 72 + 73 + 74) + (75 + 76 + 77 + 78) + ... + (74K–3 + 74K–2 + 74K–1 + 74K) = (7 + 72 + 73 + 74)(1 + 74 + 78 + ... + 74K–4). Сумма (7 + 72 + 73 + 74) = 7·400 делится на 400, откуда и вытекает доказываемое.
Решение задачи 12^*: Подставив n = 1, n = 3 и n = 4, получаем, что числа 2²·3·5a, 2·3²·5·7a и 2⁶·3·7a – целые. Значит, a – рациональное число, имеющее несократимую запись ^p/_q, где q является делителем числа НОД(2²·3·5, 2·3²·5·7, 2⁶·3·7) = 6. Итак, a = ^k/₆ при некотором целом k.
Осталось показать, что все числа такого вида подходят. Действительно, одно из трёх последовательных чисел n + 2, n + 3, n + 4 делится на 3, а одно из последовательных чисел n + 2, n + 3 делится на 2; значит, n(n + 2)(n + 3)(n + 4) делится на 6. Поэтому

– целое число.
Ответ : , где k – любое целое число.

Решение задачи 13*: Предположим, что нашлись 18 хороших чисел подряд.

Среди них найдутся три числа, делящихся на 6. Пусть это числа 6n, 6(n + 1) и

6(n + 2). Поскольку эти числа – хорошие, и в разложение каждого из них на

простые множители входят двойка и тройка, других простых делителей у них

быть не может. Лишь одно из трёх подряд идущих натуральных чисел n, n + 1,

n + 2 может делиться на 3. Значит, остальные два являются степенями двойки.

Но пары степеней двойки, отличающихся не более чем на два, – это только (1, 2)

и (2, 4); поэтому n ≤ 2. Однако тогда среди наших 18 чисел есть простое

число 13 (так как 6n ≤ 13 ≤ 6(n + 2)), не являющееся хорошим. Противоречие.

Ответ: Не могут.

Решение задачи 14*:  Докажем, что для произвольного нечётного n = 2m – 1 сумма S = 1n + 2n + ... + nn делится на 1 + 2 + ... + n = nm. Числа n и m взаимно просты, поэтому достаточно проверить, что S делится на n и на m.
   S = (1n + nn) + (2n + (n – 1)n) + ... + ((m – 1)n + (m + 1)n) + mn. Сумма в каждой скобке, кроме последней, делится на n + 1 = 2m, поэтому S делится на m.
   С другой стороны, S = (1n + (n – 1)n) + (2n + (n – 2)n) + ... + ((m – 1)n + mn) + nn, поэтому S делится на n.

Решение задачи 15*: В решении латинскими буквами везде обозначены натуральные числа.
По условию, (x – 1)3 + x3 + (x + 1)3 = y3, или 3x(x2 + 2) = y3. Значит, y делится на 3, y = 3z и   x(x2 + 2) = 9z3. Очевидно, НОД(x, x2 + 2) ≤ 2.
Пусть НОД(x, x2 + 2) = 1. Тогда либо x = 9u3 и x2 + 2 = v3, либо x = u3,  x2 + 2 = 9v3 при некоторых натуральных u, v. В первом случае 81u6 + 2 = v3, что невозможно, так как куб целого числа при делении на 9 дает остаток 0 или ±1. Аналогично, второе равенство влечёт, что u6 + 2 = 9v3, что невозможно по тем же причинам.
Итак, НОД(x, x2 + 2) = 2,  x(x2 + 2) = 9z3. Тогда x (и, следовательно, z) чётно, поэтому x(x2 + 2) делится на 8. Поскольку x2 + 2 не делится на 4, получаем, что x делится на 4.

Раздел 4. Комбинаторика. (10 часов)

На примере решенных задач видно практическое применение "Комбинаторики" в различных сферах деятельности человека, т. е. где в реальной жизни можно встретиться с комбинаторикой.

Комбинаторика играет большую роль в практической деятельности человека. Области применения комбинаторики:

учебные заведения (составление расписаний)
сфера общественного питания (составление меню)
лингвистика (рассмотрение вариантов комбинаций букв)
география (раскраска карт)
спортивные соревнования (расчёт количества игр между участниками)
производство (распределение нескольких видов работ между рабочими)
агротехника (размещение посевов на нескольких полях)
азартные игры (подсчёт частоты выигрышей)
биология (расшифровка кода ДНК)

Математика это оружие, с помощью которого человек познаёт и покоряет себе окружающий мир. Чтобы сделать в математике что-то действительно ценное, надо любить её так, как многие великие математики.

Например: Сколько двузначных чисел можно составить, используя цифры 1, 4 и 7?

Решение. Для того чтобы не пропустить и не повторить ни одно из чисел, надо выписывать их в порядке возрастания. Сначала вписываем числа, начинающиеся с цифры 1, затем с цифры 4 и, наконец, с цифры 7. Получаем следующий расклад.

11	14	17
41	44	47
71	74	77

Таким образом, из трех данных цифр можно составить всего 9 различных двузначных чисел.

Существует единый подход к решению самых разных комбинаторных задач с помощью составления специальных схем. Внешне такая схема напоминает дерево, отсюда название – дерево возможных вариантов. Решение комбинаторных задач методом составления дерева вариантов с применением правила умножения. Так, например, “дерево возможностей” помогает решать разнообразные задачи, касающиеся перебора вариантов происходящих событий. Каждый путь по этому “дереву” соответствует одному из способов выбора, число способов выбора равно числу точек в нижнем ряду “дерева”. Правило умножения заключается в том, что для того, чтобы найти число всех возможных исходов независимого проведения двух испытаний А и В, следует перемножить число всех исходов испытания А и число всех исходов испытания В.

Например: Сколько двузначных чисел можно составить, используя цифры 1, 5 и 8?

*

П

ервая цифра 1 5 8

Вторая цифра 1 5 8 1 5 8 1 5 8

Число 11 15 18 51 55 58 81 85 88

Э

та схема действительно похожа на дерево, правда, «вверх ногами» и без ствола. Знак «*» изображает корень дерева, ветви дерева – различные варианты решения. Чтобы получить двузначное число, надо сначала выбрать первую его цифру, а для нее есть три варианта: 1, 5 или 8. Поэтому из точки * проведены три отрезка и на концах поставлены цифры 1, 5 и 8.

Теперь надо выбрать вторую цифру, а для этого также есть три варианта: 1, 5 или 8. Поэтому от каждой первой цифры проведено по три отрезка, на концах которых снова записано 1, 5 или 8. Итак, получено всего 9 различных двузначных чисел. Других двузначных чисел из этих трех цифр составить невозможно.

В задачах по комбинаторике часто применяется такое понятие как факториал (в переводе с английского “factor” - “множитель”).
Факториал числа — это произведение всех натуральных чисел до этого числа включительно.

Обозначается с восклицательным знаком в конце. n! = 1 · 2 · 3 · 4 · … · (n-2) · (n-1) · n

Случай 0! определен и имеет значение 0!=1, соответствующее комбинаторной интерпретации комбинации нуля объектов, другими словами, есть единственная комбинация нуля элементов, а именно: пустое множество.

Ниже приведены значения факториалов от 0 до 10.

0! = 1
1! = 1
2! = 1 · 2 = 2
3! = 1 · 2 · 3 = 6
4! = 1 · 2 · 3 · 4 = 24
5! = 1 · 2 · 3 · 4 · 5 = 120
6! = 1 · 2 · 3 · 4 · 5 · 6 = 720
7! = 1 · 2 · 3 · 4 · 5 · 6 · 7 = 5040
8! = 1 · 2 · 3 · 4 · 5 · 6 · 7 · 8 = 40320
9! = 1 · 2 · 3 · 4 · 5 · 6 · 7 · 8 · 9 = 362880
10! = 1 · 2 · 3 · 4 · 5 · 6 · 7 · 8 · 9 · 10 = 3628800

Свойство факториала: (n + 1)! = (n + 1) · n!

Например: (5 + 1)! = (5 + 1) · 5!

Действительно 6! = (1 · 2 · 3 · 4 · 5) · 6 = 720

А значение (1 · 2 · 3 · 4 · 5) = 5! = 120

В комбинаторике решаются задачи, связанные с рассмотрением множеств и составлением различных комбинаций из элементов этих множеств. В зависимости от правил составления можно выделить три типа комбинаций: перестановки, размещения, сочетания.

2. Примеры решения задач

1. В школьной столовой на первое можно заказать борщ, солянку, грибной суп, на второе - мясо с макаронами, рыбу с картошкой, курицу с рисом, а на третье - чай и компот. Сколько различных обедов можно составить из указанных блюд?

1 способ. Перечислим возможные варианты

Чай(Ч) Компот (К)	Мясо с макаронами(М)	Рыба с картошкой(Р)	Курица с рисом(Кр)
Борщ (Б)	БМЧ/ БМК	БРЧ/БРК	БКрЧ/БКрК
Солянка(С)	СМЧ/ СМК	СРЧ/СРК	СКрЧ/СКрК
Грибной суп(Г)	ГМЧ/ГМК	ГРЧ/ГРК	ГКрЧ/ГКрК

18 вариантов.

2 способ. Дерево возможностей.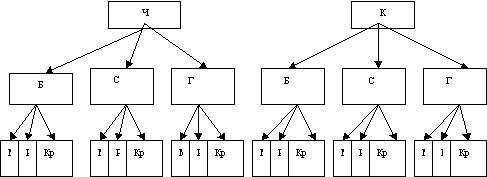

3 способ. Используя правило умножения, получаем: 3х3х2=18

2. Свете на день рождения подарили 4 плюшевых игрушки, 2 мяча и 5 кукол. Мама положила все игрушки в большую коробку. Сколькими способами Света сможет достать из коробки 1 плюшевую игрушку, 1 мяч и 1 куклу?

1 способ. Обозначим мячи - М1, М2, игрушки- И1,И2,И3, И4, куклы- К1,К2, К3, К4, К5. Перечислим возможные варианты:

М1-И1-К1, М1-И1-К2, М1-И1-К3, М1-И1-К4, М1-И1-К5,
М1-И2-К1, М1-И2-К2, М1-И2-К3, М1-И2-К4, М1-И2-К5,
М1-И3-К1, М1-И3-К2, М1-И3-К3, М1-И3-К4, М1-И3-К5,
М1-И4-К1, М1-И4-К2, М1-И4-К3, М1-И4-К4, М1-И4-К5
М2-И1-К1, М2-И1-К2, М2-И1-К3, М2-И1-К4, М2-И1-К5,
М2-И2-К1, М2-И2-К2, М2-И2-К3, М2-И2-К4, М2-И2-К5,
М2-И3-К1, М2-И3-К2, М2-И3-К3, М2-И3-К4, М2-И3-К5,
М2-И4-К1, М2-И4-К2, М2-И4-К3, М2-И4-К4, М2-И4-К5

Ответ: 40 вариантов.

2 способ. Используя правило умножения, получаем: 2х4х5= 40

3. Сколько четных двузначных чисел можно составить из цифр 0, 2, 3, 6, 7, 9?

1 способ. Перечислим возможные варианты.

	0	2	6
2	20	22	26
3	30	32	36
6	60	62	66
7	70	72	76
9	90	92	96

2 способ. Дерево возможностей.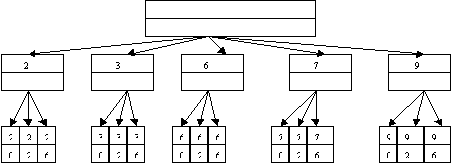

3 способ. Используя правило умножения, получаем: 5х3=15 .

4. Саша, Петя, Денис, Оля, Настя часто ходят в кафе. Каждый раз, обедая там, они рассаживаются по-разному. Сколько дней друзья смогут это сделать без повторения?

1 способ. Пронумеруем стулья, на которых должен сесть каждый, и будем считать, что они рассаживаются поочередно:

№1 - Саша - есть возможность выбрать из 5 вариантов (стульев)
№2 - Петя - 4 варианта
№3- Денис - 3 варианта
№4- Оля - 2 варианта
№5 - Настя- 1 вариант

Используя правило умножения, получаем: 5х4х3х2х1=120

2 способ. Решаем, используя понятие факториала: 5!=120

6. Из учащихся пяти 11 классов нужно выбрать двоих дежурных. Сколько пар дежурных можно составить (ученики в паре не должны быть из одного класса)?

1 способ. Перечислим возможные варианты состава пары:

11А-11Б, 11А-11В, 11А-11Г, 11А-11Д,
11Б-11В, 11Б-11Г, 11Б-11Д, 11В-11Г, 11В-11Д, 11Г-11Д

Ответ: 10 пар.

2 способ. Из пяти классов нужно выбрать 2 дежурных.
Число элементарных событий =

= 10

7. В 8 “а” классе лучше всех математику знают 5 учеников: Вася, Дима, Олег, Катя и Аня. На олимпиаду по математике нужно отправить пару, состоящую из 1 мальчика и 1 девочки. Сколькими способами учительница может эту пару выбрать?

1 способ. Обозначим имена детей первыми заглавными буквами.
Получаем следующие пары:
В-К, В-А, Д-К, Д-А, О-К, О-А.

Ответ: 6 пар.

2 способ. Мальчиков 3, из них 1 можно выбрать

, девочек 2, из них можно 1 выбрать

, используя правило умножения, получаем:

= 6

8. В соревнованиях по фигурному катанию принимали участие россияне, итальянцы, украинцы, немцы, китайцы и французы.

Сколькими способами могут распределится места по окончании соревнований?
Обозначим участников по первой заглавной букве страны и пронумеруем: Р1, И2, У3, Н4,К5, Ф6
Р1 - имеют возможность занять с1-6 места, т.е. 6 вариантов
И2 - 5 вариантов
У3- 4 варианта
Н4- 3 варианта
К5- 2 варианта
Ф6- 1 вариант
Используя правило умножения, получаем: 6х5х4х3х2х1= 720

2 способ. Используя понятие факториала, получаем: 6!=720

9. В 9 “б” классе 6 человек (Галя, Света, Катя, Оля, Максим, Витя) учатся на все пятерки. Департамент образования премировал лучших учащихся путевками в Анапу. Но, к сожалению, путевок всего четыре. Сколько возможно вариантов выбора учеников на отдых?

Обозначим первыми заглавными буквами имен учащихся.
Возможны следующие тройки:
Г-С-К-О, Г-С-К-М, Г-С-К-В,
Г-С-О-М, Г-С-О-В, Г-С-М-В
С-К-О-М, С-К-О-В, С-К-М-В,
К-О-М-В, С-О-М-В, Г-К-О-В,
Г-К-О-В, Г-О-М-В, Г-К-М-В

2 способ. Из 6 человек нужно выбрать 4, число элементарных событий равно

= 15

10. Пете на день рождения подарили 7 новых дисков с играми, а Вале папа привез 9 дисков из командировки. Сколькими способами они могут обменять 4 любых диска одного на 4 диска другого?

Вычислим, сколько четверок из 7 дисков можно составить у Пети:

=35, число четверок у Вали из 9 дисков -

= 126
По правилу умножения находим число обменов 35х126=4410

11. Войсковое подразделение состоит из 5 офицеров, 8 сержантов и 70 рядовых. Сколькими способами можно выделить отряд из 2 офицеров, 4 сержантов и 15 рядовых?

Из 5 офицеров выбрать 2 можно с помощью числа сочетаний

=10 способами, из 8 сержантов 4 -

=70, из 70 рядовых 15 -

. По правилу умножения находим число выбора отряда:
10х70х

= 700х

12. В ювелирную мастерскую привезли 6 изумрудов, 9 алмазов и 7 сапфиров. Ювелиру заказали браслет, в котором 3 изумруда, 5 алмазов и 2 сапфиров. Сколькими способами он может выбрать камни на браслет?

Из 6 изумрудов 3 он может выбрать

=20 способами, из 9 алмазов 5 -

=126, из 7 сапфиров 2 -

=21. По правилу умножения находим число вариантов 20х126х21=52920

13. На выборах победили 9 человек - Сафонов, Николаев, Петров, Кулаков, Мишин, Гусев, Володин, Афонин, Титов. Из них нужно выбрать председателя, заместителя и профорга. Сколькими способами это можно сделать?

Здесь речь идет о размещениях

Можно было решать по-другому. На должность председателя выбираем из 9 человек, на заместителя - из 8, на профорга - из 7
По правилу умножения получаем 9х8х7=504

14. В районе построили новую школу. Из пришедших 25 человек нужно выбрать директора школы, завуча начальной школы, завуча среднего звена и завуча по воспитательной работе. Сколькими способами это можно сделать?

На должность директора выбираем из 25 человек, на завуча начальной - из 24, завуча среднего звена - из 23, завуча по воспитательной работе - 22. По правилу умножения получаем:
25х24х23х22 = 303600
Или, зная формулу размещения, получаем

15. В студенческом общежитии в одной комнате живут трое студентов Петя, Вася и Коля. У них есть 6 чашек, 8 блюдец и 10 чайных ложек (все принадлежности отличаются друг от друга). Сколькими способами ребята могут накрыть стол для чаепития (так, что каждый получит чашку, блюдце и ложку)?

Для Пети набор можно набрать 6х8х10=480 способами, для Васи - 5х7х9=315, для Коли - 4х6х8=192. По правилу умножения получаем
480х315х192=29030400 способами.

16. В кабинете заведующего ювелирного магазина имеется код, состоящий из двух различных гласных букв русского алфавита, за которой следуют 3 различные цифры. Сколько вариантов придется перебрать мошеннику, чтобы раздобыть драгоценности, которые там хранятся?

В русском языке 9 гласных букв - а, е, е, и, о, у, э, ю, я. Выбрать из них 2 можно

=36 способами. Из 10 цифр выбрать 3 можно

=120 способами. Применяя правило умножения, получаем:
36х120=4320

17. Сколькими способами можно составить трехцветный флаг из полос разной ширины, если имеются материи из 8 тканей?
Эта задача на размещение

Другой способ решения.
1цвет выбирается из 8 тканей 8 способами
2цвет выбирается 7 способами
3 цвет - 6способами
Используя правило умножения, получаем 8х7х6=336 способов.

18. В 9 классе 15 предметов. Завучу школы нужно составить расписание на субботу, если в этот день 5 уроков. Сколько различных вариантов расписания можно составить, если все уроки различные?

Из 15 предметов 5 любых можно выбрать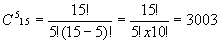

19. В огороде у бабушки растут 3 белые, 2 алые и 4 чайных розы. Сколькими различными способами можно составить букет из трех роз разного цвета?

1 способ. Обозначим белые - Б1, Б2, Б3, алые - А1,А2, чайные - Ч1, Ч2, Ч3,Ч4
Перечислим возможные варианты
Б1-А1-Ч1, Б1-А1-Ч2, Б1-А1-Ч3, Б1-А1-Ч4, Б1-А2-Ч1,Б1-А2-Ч2, Б1-А2-Ч3, Б1-А2-Ч4
Б2- А1-Ч1, Б2-А1-Ч2, Б2-А1-Ч3, Б2-А1-Ч4, Б2-А2-Ч1,Б2-А2-Ч2, Б2-А2-Ч3, Б2-А2-Ч4
Б3- А1-Ч1, Б3-А1-Ч2, Б3-А1-Ч3, Б3-А1-Ч4, Б3-А2-Ч1,Б3-А2-Ч2, Б3-А2-Ч3, Б3-А2-Ч4

Ответ: 24 варианта.

2способ. Дерево возможностей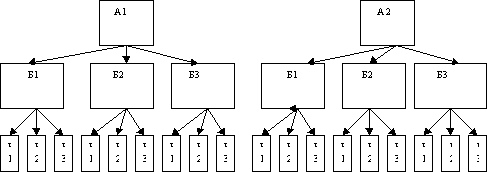

3 способ. Используя правило умножения, получаем: 2х3х4=24

20. К 60-летию Победы группа школьников отправилась по местам боевых действий в Смоленской области. Они планировали осуществить поход по маршруту деревни Сосновка-Быковка- Масловка- Видово. Из С в Б можно проплыть по реке или пройти пешком, из Б в М- пешком или на автобусе, из М в В - по реке, пешком или автобусе. Сколько вариантов похода есть у щкольников?

1 способ. Обозначим СБ - путь из Сосновки в Бытовку, ВГ - путь из Быковки в Масловку, МВ - путь из Масловки в Видово.
По реке -Р, пешком - П, на автобусе - А
Перечислим возможные варианты:
СБР- БМП-МВР, СБР- БМП-МВП, СБР- БМП-МВА
СБР-БМА-МВР, СБР-БМА-МВП, СБР-БМА-МВА
СБА- БМП-МВР, СБА- БМП-МВП, СБА- БМП-МВА
СБА-БМА-МВР, СБА-БМА-МВП, СБА-БМА-МВА
Ответ: 12 вариантов.

2 способ. Дерево возможностей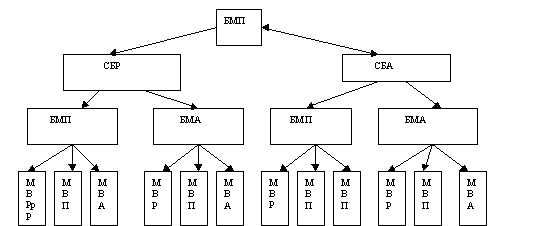

Список использованной литературы:

Бахтина, Т. П. Готовимся к олимпиадам, турнирам и математическим боям / Т. П. Бахтина. — Мн.: АВЕРСЭВ, 2002. — 253 с.
Горбачев, Н.В. Сборник олимпиадных задач по математике / Н. В. Горбачев. — Москва: Просвещение, 2004. — 600 с.
Клименченко, Д. В. Задачи по математике для любознательных / Д. В. Клименченко. — Москва: Просвещение, 1992. — 192 с.
Шарыгин, И. Ф. Задачи на смекалку / И. Ф. Шарыгин, А. В. Шевкин. — М.: Просвещение, 2003. — 93 с.
Петраков А.С.«Математика для любознательных», Москва:Просвещение, 2002г.
Атанасян Л.С. Геометрия 7-9. М.: Просвещение, 2005. - 335 с.
Гусев В.А., Медяник А.И. Дидактические материалы по геометрии для 7 класса. М.: Просвещение, 1991. – 80с.
Далингер В.А. Планиметрические задачи на построение. Омск: Изд-во ОГПИ, 1999. - 78 с.
Ильина Н.И. Геометрические построения на плоскости. М.: Школа - пресс, 1997. - 172 с.
Манин И.Ю. О разрешимости задач на построение с помощью циркуля и линейки // Энциклопедия элементарной математики. М.: Физматгиз, 1963. Т. 4: Геометрия. С. 205-227.
Олимпиадные задания по математике. 5–8класс/авт.-сост. С.П. Ковалева.–Волгоград: Учитель, 2007.–88с.
Погорелов А.В. Геометрия, 7–11. М.: Просвещение, 1992
Прасолов В.В. Три классические задачи на построение. М.: Наука, 1992. 80 с.
Энциклопедия для детей. Т. 11. Математика/Ред. коллегия: М.Аксенова, В.Володин и др. – М.: Аванта+, 2005.
Коренева В.Е. Решение задач на построение методом спрямления. Математика в школе.1995г. №5
Клименченко С.В., Цикунова Т.Д. Задачи на построение треугольников по некоторым данным точкам. Математика в школе. 1990г. №1
Белошистая А.В. Задачи на построение в школьном курсе геометрии. Математика в школе. 2002г. №9