Блок 2.Методы соц исследований. Программа соц исследования
 Скачать 108.54 Kb. Скачать 108.54 Kb.
|
|
20. Меры вариаций рядов распределений. Меры вариации – это показатели, которые учитывают количество отклонений от мер центральной тенденции (Меры центральной тенденции – это показатели, которые характеризуют всю изучаемую совокупность респондентов одним числом.Например, средний возраст, модальная национальность, медианный доход.). Меры вариации — показатели колеблемости значений некоторого признака у индивидов данной совокупности. Одна из простейших мер — вариационный размах, равный разности крайних (наибольшего и наименьшего) значений признака в данной совокупности. Важнейшим показателем колеблемости является дисперсия. Т. к. из-за компенсации отклонений индивидуальных значений от М ( Меры центральной тенденции), имеющих разные знаки, сумма всех отклонений равна нулю, в качестве М. в. используется сумма квадратов отклонений, приходящаяся на одно наблюдение. Эта величина и называется дисперсией (D). Дисперсия – это среднеарифметическое квадратов отклонений вариантов от среднего арифметического значения признака для данной совокупности, т.е. - Среднее арифметическое отклонение *100% - процент отклонения от среднего арифметического ( - коэффициент вариации) Различают: - общую дисперсию - измеряет вариацию признака по всей совокупности в целом под влиянием всех факторов, обуславливающих эту вариацию. Она равняется среднему квадрату отклонений отдельных значений признака х от общего среднего значения х и может быть определена как простая дисперсия или взвешенная дисперсия. - внутригрупповая дисперсию - Внутригрупповая дисперсия характеризует случайную вариацию, т.е. часть вариации, которая обусловлена влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Внутригрупповая дисперсия измеряет вариацию признака внутри группы и определяется по формуле: 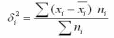 где хi — групповая средняя; ni — число единиц в группе. - среднюю из внутригрупповых дисперсий - средняя из внутри групповых дисперсий отражает случайную вариацию, т. е. ту часть вариации, которая происходила под влиянием всех прочих факторов, за исключением фактора группировки. Она рассчитывается по формуле: 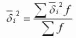 - межгрупповая дисперсию - характеризует систематическую вариацию результативного признака, которая обусловлена влиянием признака-фактора, положенного в основание группировки. Она равняется среднему квадрату отклонений групповых средних от общей средней. Межгрупповая дисперсия рассчитывается по формуле:  Согласно правилу сложения дисперсий общая дисперсия равна сумме средней из внутригрупповых и межгрупповых дисперсий: 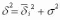 Смысл этого правила заключается в том, что общая дисперсия, которая возникает под влиянием всех факторов, равняется сумме дисперсий, которые возникают под влиянием всех прочих факторов, и дисперсии, возникающей за счет фактора группировки. Пользуясь формулой сложения дисперсий, можно определить по двум известным дисперсиям третью неизвестную, а также судить о силе влияния группировочного признака. Свойства дисперсии: 1. Если все значения признака уменьшить (увеличить) на одну и ту же постоянную величину, то дисперсия от этого не изменится. 2. Если все значения признака уменьшить (увеличить) в одно и то же число раз n, то дисперсия соответственно уменьшится (увеличить) в n^2 раз. Особаяценность Д., вычисленной по выборке, состоит в том, чтоонаявляетсянесмещеннойоценкой Д. генеральнойсовокупности - ср.: выборочноестандартноеотклонениеявляетсясостоятельной, носмещеннойоценкой стандартного отклонениягенеральнойсовокупности. 21. Корреляционная зависимость между признаками Конспект Корреляционная зависимость – это вид статистической зависимости, когда каждому значению х соответствует целый ряд значений у, но с изменением значений х меняется не только ряд распределения у, но и его средняя. Предположительно, корреляционную зависимость можно установить на основании корреляционной таблицы. Но также следует проводить корреляционный анализ. Это статистическая процедура установления зависимостей между признаками. Применяется к 2-мерным распределениям. Требования к корреляционному анализу: должно быть не менее 100 опрошенных внутриклеточные частоты не должны быть нулевыми (должно быть не менее 5 опрошенных) нужно проследить, для каких типов признаков годится тот или иной коэффициент корреляции необходимо обращать внимание на уровень значимости того или иного коэффициента корреляционная зависимость между признаками не тождественная причинно-следственной (логической) зависимости. При помощи корреляционного анализа мы можем найти значения различных коэффициентов корреляции. Как правило, все они принимают значения от -1 до + 1. Отрицательные значения свидетельствуют о наличии полной обратной зависимости, а положительные значения говорят нам о полной прямой зависимости. 0 – означает отсутствие связи между признаками. Критерий хи-квадрат принимает значения от 0 до + бесконечности. Он используется только при большом числе наблюдений. Для того чтобы определить, насколько тесная связь между признаками, используются статистические таблицы и вычисляется погрешность. Принципы построения коэффициентов корреляции: принцип сравнения эмпирической таблицы с теоретической. Теоретическая таблица – таблица, где связь между признаками нулевая, а внутриклеточные частоты располагаются пропорционально маргиналам. принцип ковариации – как изменение одного признака влияет на изменение другого. 22. Коэффициенты корреляции и способы их построения Корреляционная зависимость – вид статистической зависимости, где каждому значению Х соответствует целый ряд значений У, но в корреляционной зависимости с изменением значения Х меняется не только ряд значений У, но и его средние. Корреляция устанавливает факт зависимости (изменения одного признака вызовет ли изменения второго). Коэффициенты корреляции стремятся получить значения от -1 до +1: -1 – полная обратная зависимость (увеличение одного признака ведёт к уменьшению другого) +1 – увеличение одного признака ведёт к увеличению другого признака. 0 – связь отсутствует. Коэффициенты корреляции — меры плотности корреляционной связи, когда каждому значению одного признака соответствуют различные, но близкие значения другого признака, т. е. тесно располагающиеся около своей средней величины,— связь более плотная. Коэффициент Пирсона—Браве r является мерой связи при линейной корреляции. Все его значения заключены между —1 и +1, причем крайние значения соответствуют линейной функциональной связи между признаками. Значение r =0 означает отсутствие линейной связи, по при r=0 может иметь место нелинейная связь, даже функциональная. Мерой плотности нелинейной связи является корреляционное отношение R принимающее значения между 0 и 1. Значение 0 соответствует отсутствию связи. Чем больше R тем теснее связь между признаками. Значение 1 соответствует функциональной связи. Модуль r всегда не превосходит R (для одной и той же корреляционной таблицы), r и R применяются дляописании количественных признаков. Если изучаемые индивиды охарактеризованы лишь по относительной интенсивности свойства (признака), т. е. только ранжированы, то для описания связи используются коэффициенты ранговой корреляции. Если при описании объектов удается определить лишь наличие или отсутствие у них признака, либо если изучается связь между альтернативными признаками, то корреляционные таблицы становятся четырехклеточнымпи. В таких случаях можно применять коэффициенты ассоциации Q и контингенции Ф. Ряд К. к. основан на критерии Пирсона. Это коэффициент сопряженности Пирсона С, теоретически более предпочтительный коэффициент Чупрова Т. Коэффициенты частной корреляции позволяют изучать связи между признаками при элиминировании влияния некоторых других признаков. Если устраняется влияние одного признака, то говорят о частных К. к. первого порядка. Они выражаются через обычные коэффициенты парной корреляции. Логика частной корреляции такова: если при устранении некоторого признака коэффициент корреляции двух данных признаков увеличивается, то такой признак ослабляет связь, если же коэффициент корреляции уменьшается, то устраняемый признак в определенной мере обуславливает связь. (В предельном случае, если устранение признака обращает коэффициент корреляции в нуль, то данный признак обуславливает связь данных признаков, т. е. это связь сопутствия). Например, при изучении корреляции между производительностью труда и возрастом рабочих была установлена положительная связь. На производительность влияет и стаж работы, который оказывается в положительной корреляции и с возрастом, и с производительностью. При элиминировании стажа оказалось, что связь между производительностью и возрастом отрицательная, а между производительностью труда и стажем (при элиминировании возраста) — положительная и еще более тесная. Коэффициент корреляции Пирсона (r-Пирсона) - коэффициент, используемый для установления меры взаимосвязи между значениями переменных изучаемых выборок, численность которых достаточно большая, а распределение соответствует нормальному. Коэффициент корреляции Спирмена (r-Спирмена) - коэффициент, используемый для установления меры взаимосвязи между значениями переменных изучаемых выборок, численность которых незначительная ( 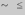 40 человек в обеих выборках), и распределение не соответствует нормальному (в случае ненормальности распределения одной из выборок принимается решение о выборе именно r-Спирмена). 40 человек в обеих выборках), и распределение не соответствует нормальному (в случае ненормальности распределения одной из выборок принимается решение о выборе именно r-Спирмена).Принципы построения: принцип сравнения эмпирической таблицы с теоретической ( в последней связи пока нет). Теоретическая таблица – внутриклеточные частоты должны располагаться пропорционально маргиналам. Принцип ковариации (принцип одновременного изменения признака – как изменения одного признака вызывают изменения другого. 23. Кластерный анализ данных в социологическом исследовании. Кластерный анализ - это разбиение совокупности опрошенных на однородные группы таким образом, чтобы различия между представителями разных групп были максимальными. Если, например, мы хотим построить группы опрошенных по признакам x, y и z, то каждого респондента мы рассматриваем как точку в признаковом пространстве xyz, где координатами этой точки являются ответы на вопросы x, y, z. Картина может вырисовываться самая разнообразная: от облака точек, равномерно распределенных в этом пространстве, до выделяющихся групп, в которых точки находятся достаточно близко друг к другу. Процедура построения кластеров с помощью SPSS. Первое, что нужно определить – это выбор расстояния между объектами (a2+b2) (эвклидово расстояние) В качестве меры близости можно использовать эвклидову метрику. Далее выбираем алгоритм поиска кластеров: - алгомеративные алгоритмы - дивизимные алгоритмы Указываем также количество раз (итерация), которое будет работать этот алгоритм. Основные показатели, которые участвуют при результатах кластерного анализа. 1) % дисперсии ряда (% опрошенных, которые попали в кластеры). Оптимальный вариант 60-70 % 2) кластерная переменная (это еще один признак, который взаимодействует со всеми вопросами кластеров. 24. Факторныйанализ в социологии. Факторный анализ это процедура, с помощью которой большое число переменных, относящихсяк имеющимся наблюдениям сводит к меньшему кол-ву независимых влияющих величин,называемых факторами. При этом в один фактор объединяются переменные, сильнокоррелирующие между собой. Т. о., целью Ф. А. явл-я нахождение таких комплексныхфакторов, которые как можно более полно объясняют наблюдаемые связи между переменными,имеющимися в наличии. Факторный анализ позволяет решить две важные проблемы исследователя: описать объект измерения всесторонне и в то же время компактно. С помощью факторного анализа возможно выявление скрытых переменных факторов, отвечающих за наличие линейных статистических связей корреляций между наблюдаемыми переменными. Можно выделить 2 цели Факторного анализа: определение взаимосвязей между переменными, их классификация. сокращение числа переменных. Для выявления наиболее значимых факторов и, как следствие, факторной структуры, наиболее оправданно применять метод главных компонентов (МГК). Суть данного метода состоит в замене коррелированных компонентов некоррелированными факторами. Другой важной характеристикой метода является возможность ограничиться наиболее информативными главными компонентами и исключить остальные из анализа, что упрощает интерпретацию результатов. Достоинство МГК также в том, что он — единственный математически обоснованный метод факторного анализа. Факторный анализ может быть: 1) разведочным — он осуществляется при исследовании скрытой факторной структуры без предположения о числе факторов и их нагрузках; 2) конфирматорным, предназначенным для проверки гипотез о числе факторов и их нагрузках. Практическое выполнение факторного анализа начинается с проверки его условий. В обязательные условия факторного анализа входят: все признаки должны быть количественными; число признаков должно быть в два раза больше числа переменных; выборка должна быть однородна; исходные переменные должны быть распределены симметрично; факторный анализ осуществляется по коррелирующим переменным. Главной проблемой факторного анализа является выделение и интерпретация главных факторов. При отборе компонент исследователь обычно сталкивается с существенными трудностями, так как не существует однозначного критерия выделения факторов, и потому здесь неизбежен субъективизм интерпретаций результатов. Существует несколько часто употребляемых критериев определения числа факторов. Некоторые из них являются альтернативными по отношению к другим, а часть этих критериев можно использовать вместе, чтобы один дополнял другой: Критерий Кайзера или критерий собственных чисел. Этот критерий предложен Кайзером, и является, вероятно, наиболее широко используемым. Отбираются только факторы с собственными значениями равными или большими 1. Этоозначает, что если фактор не выделяет дисперсию, эквивалентную, по крайней мере, дисперсии одной переменной, то он опускается. Критерий каменистой осыпи или критерий отсеивания. Он является графическим методом, впервые предложенным психологом Кэттелом. Собственные значения возможно изобразить в виде простого графика. Кэттел предложил найти такое место на графике, где убывание собственных значений слева направо максимально замедляется. Предполагается, что справа от этой точки находитсятолько «факториальная осыпь» — «осыпь» является геологическим термином, обозначающим обломки горных пород, скапливающиеся в нижней части скалистого склона. Однако этот критерий отличается высокой субъективностью и, в отличие от предыдущего критерия, статистически необоснован. Недостатки обоих критериев заключаются в том, что первый иногда сохраняет слишком много факторов, в то время как второй, напротив, может сохранить слишком мало факторов; однако оба критерия вполне хороши при нормальных условиях, когда имеется относительно небольшое число факторов и многопеременных. На практике возникает важный вопрос: когда полученное решение может быть содержательно интерпретировано. В этой связи предлагается использовать ещё несколько критериев. Критерий значимости. Он особенно эффективен, когда модель генеральной совокупности известна и отсутствуют второстепенные факторы. Но критерий непригоден для поиска изменений в модели и реализуем только в факторном анализе по методу наименьших квадратов или максимального правдоподобия. Критерий доли воспроизводимой дисперсии. Факторы ранжируются по доле детерминируемой дисперсии, когда процент дисперсии оказывается несущественным, выделение следует остановить. Желательно, чтобы выделенные факторы объясняли более 80 % разброса. Недостатки критерия: во-первых, субъективность выделения, во-вторых, специфика данных может быть такова, что все главные факторы не смогут совокупно объяснить желательного процента разброса. Поэтому главные факторы должны вместеобъяснять не меньше 50,1 % дисперсии. Критерий интерпретируемости и инвариантности. Данный критерий сочетает статистическую точность с субъективными интересами. Согласно ему, главные факторы можно выделять до тех пор, пока будет возможна их ясная интерпретация. Она, в свою очередь, зависит от величины факторных нагрузок, то есть если в факторе есть хотябы одна сильная нагрузка, он может быть интерпретирован. Возможен и обратный вариант — если сильные нагрузки имеются, однако интерпретация затруднительна, от этой компоненты предпочтительно отказаться. Методы факторного анализа: метод главных компонент; корреляционный анализ; метод максимального правдоподобия. |
