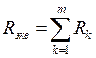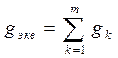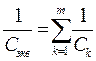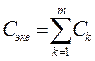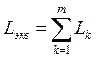Электротехника ответы. Простейшая эл цепь и отношения в ней

• Название: Простейшая эл цепь и отношения в ней
• Дата: 27.06.2022
• Размер: 5.18 Mb.
• Имя файла: Электротехника ответы.docx
• Тип: Документы; #616641
• страница: 1 из 3

• 
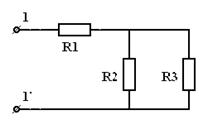
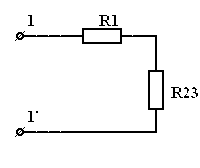
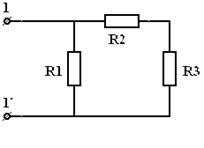
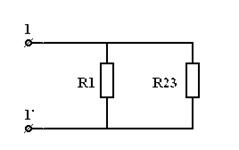
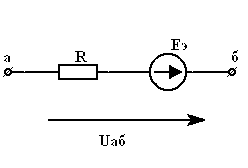
  1. простейшая эл цепь и отношения в ней.
  

Электрическая цепь – это совокупность устройств, по которым течет электрический ток.
По какому фундаментальному признаку можно разделить все цепи электрического тока? По тому же, что и ток! Есть цепи постоянного тока, а есть – переменного. В цепи постоянного тока он не меняет своего направления, полярность источника постоянна. Переменный же ток периодически изменяется во времени как по направлению, так и по величине.
Все элементы электрических цепей можно разделить на активные и пассивные. Активные элементы цепи – это те элементы, которые индуцируют ЭДС. К ним относятся источники тока, аккумуляторы, электродвигатели. Пассивные элементы – соединительные провода и электроприемники. Приемники и источники тока, с точки зрения топологии цепей, являются двухполюсными элементами (двухполюсниками). Для их работы необходимо два полюса, через которые они передают или принимают электрическую энергию. Устройства, по которым ток идет от источника к приемнику, являются четырехполюсниками. Чтобы передать энергию от одного двухполюсника к другому им необходимо минимум 4 контакта, соответственно для приема и передачи. Резисторы – элементы электрической цепи, которые обладают сопротивлением. Вообще, все элементы реальных цепей, вплоть до самого маленького соединительного провода, имеют сопротивление. Однако в большинстве случаев этим можно пренебречь и при расчете считать элементы электрической цепи идеальными. Существуют условные обозначения для изображения элементов цепи на схемах.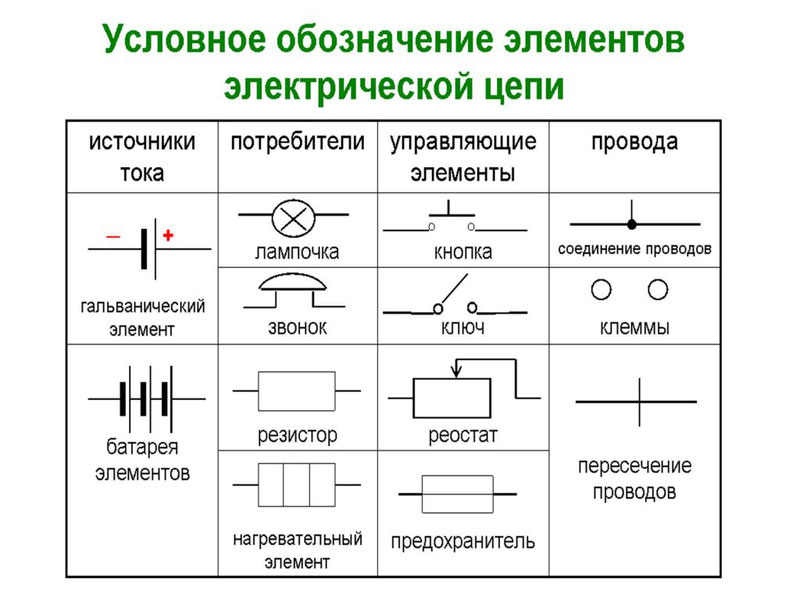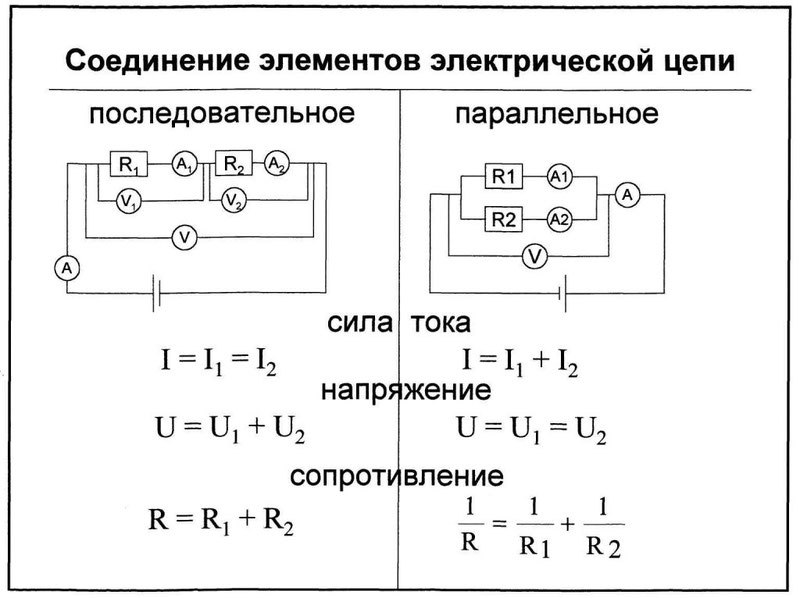

При решении задач и анализе схем используют следующие понятия: Ветвь – такой участок цепи, вдоль которого течет один и тот же ток; Узел – соединение ветвей цепи; Контур – последовательность ветвей, которая образует замкнутый путь. При этом один из узлов является как началом, так и концом пути, а другие узлы встречаются в контуре только один раз.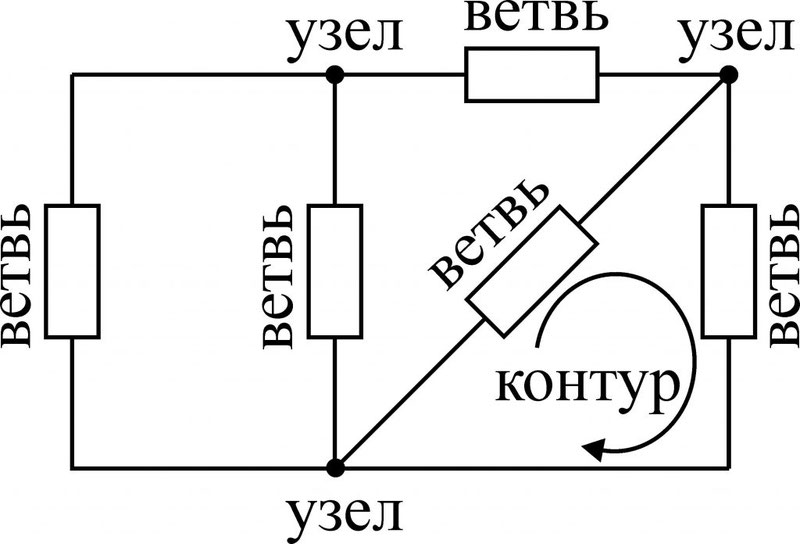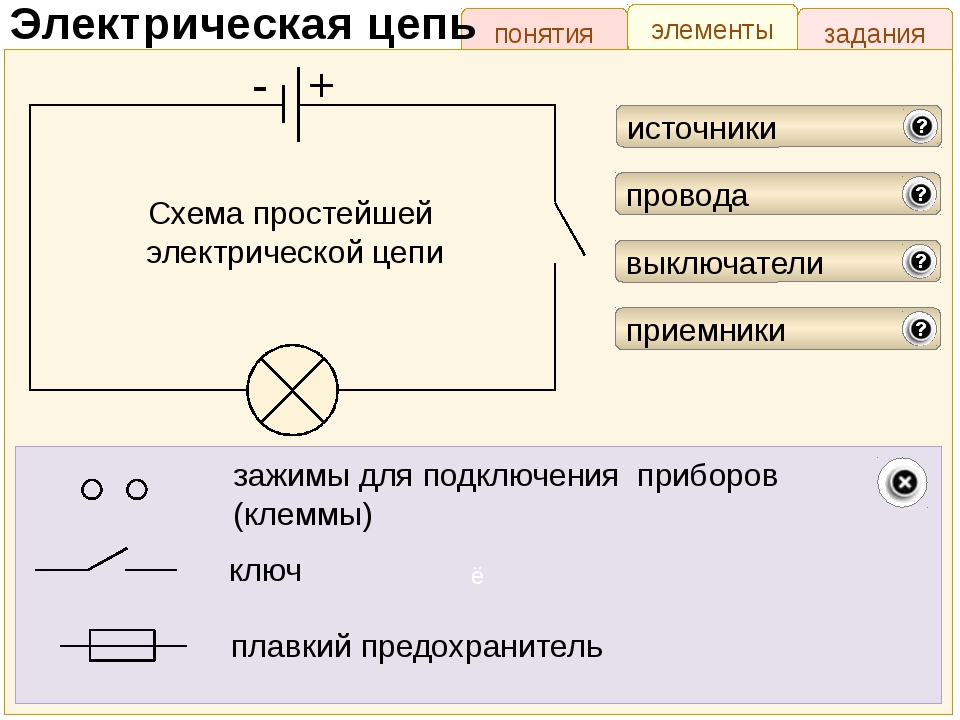

• 
  2) режимы работы эл цепи
  

Различают четыре основных режима работы электрической цепи:

- номинальный режим;

- режим холостого хода; - режим короткого замыкания;

- согласованный режим работы.

1. Номинальный режим характеризуется тем, что токи, напряжения, мощности всех элементов электрической цепи соответствуют их номинальным значениям Iном, Uном, Pном, установленным заводом-изготовителем. В этом режиме гарантируется надежная работа электрооборудования в течение длительного времени. Номинальные значения напряжения, тока и мощности берут за основу при расчетах электрических схем. По номинальному напряжению рассчитывают изоляцию проводов и отдельных устройств. По номинальному току определяют допустимый нагрев всех элементов. Нормально работает устройство когда ном I ≤ I . Для источника электроэнергии номинальная мощность Pном – это мощность, которую он отдает потребителю при Uном и Iном. На внешней характеристике источника (рис.1.8) его номинальному режиму работы соответствует точка 2. Номинальная мощность приемных устройств - это электрическая мощность, потребляемая при номинальном напряжении, т.е. ном ном ном P = U I .

2. Режим холостого хода возникает при отключении нагрузки, при обрывах цепи. В этом режиме можно принять сопротивление приемника Rпр бесконечно большим, а ток в цепи Iх = 0. Напряжение на зажимах генерирующего устройства в режиме холостой ход в соответствии с (1.15) Uх = E. На внешней характеристике источника (рис.1.8) режиму холостой ход соответствует точка 1. Этот режим используется на практике для измерения Е источника, которую определяют, подключив к его выходным зажимам электроизмерительный прибор – вольтметр. 16

3. Режим короткого замыкания создается при замыкании накоротко выходных зажимов источника или входных зажимов приемного устройства (точки А и Б или а и б на рис.1.7). В этом режиме можно принять сопротивление приемника Rпр , равным нулю Rпр = 0. При этом напряжение на зажимах генератора также равно нулю Uг = 0. Тогда ток короткого замыкания определяется только небольшим внутренним сопротивлением источника: Iк = E / R0 и значительно превышает номинальный ток. На внешней характеристике источника (рис.1.8) режиму короткого замыкания соответствует точка 4. Большой ток короткого замыкания приводит к быстрому чрезмерному нагреву генератора и выходу его из строя. В большинстве электротехнических устройств короткие замыкания нежелательны, т.к. возрастание тока ведет к резкому увеличению выделения тепла в токоведущих частях и, следовательно, к выходу из строя электроустановок. Поэтому режим короткого замыкания является аварийным режимом и недопустим при эксплуатации электротехнических устройств и электрических цепей.

4. Согласованный режим характеризуется максимально возможной мощностью передача энергии от источника к потребителю. Это возможно только при определенном соотношения сопротивлений приемника и источника. Если пренебречь величиной Rл, то есть принять Rл=0, то ток в цепи




3)эквивалентное преобразование цепей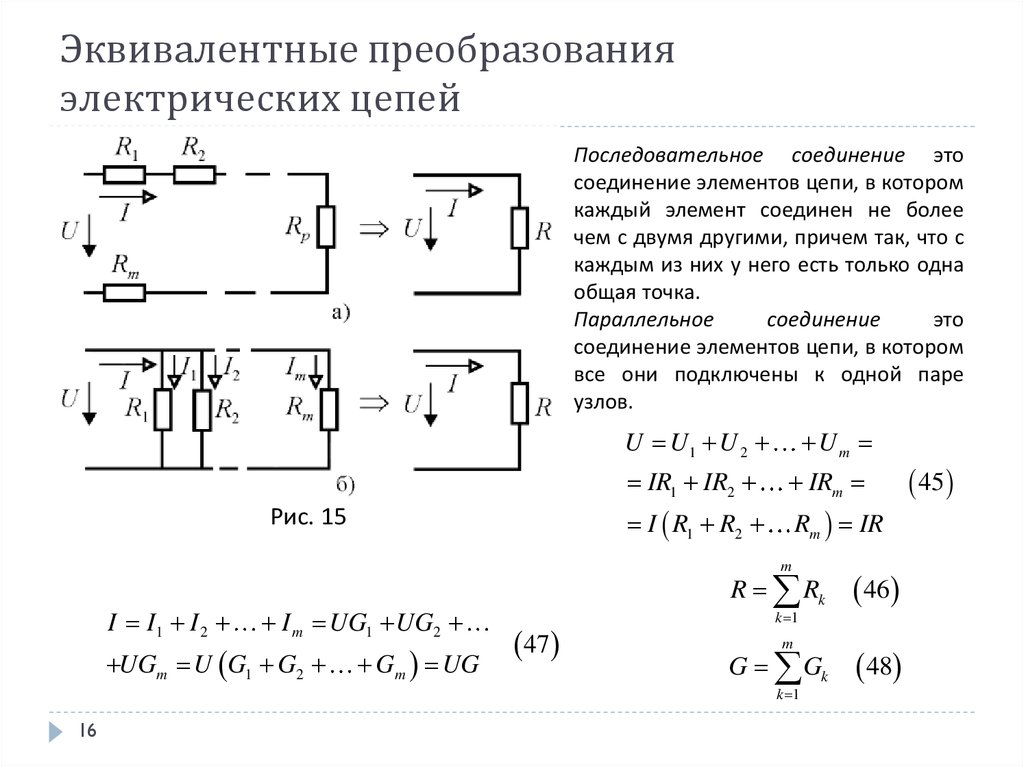

• 
  4)Эквивалентное преобразование цепей
  
• 
  Преобразование электрической цепи считается эквивалентным, в том случае, если при замене участка рассматриваемой электрической цепи более простыми электрические токи и напряжения участка, который не был преобразован, остаются неизменными. На практике, при расчетах электрических цепей используется преобразование со смешанным соединением элементов, представляющее собой сочетание простых параллельных и последовательных соединений.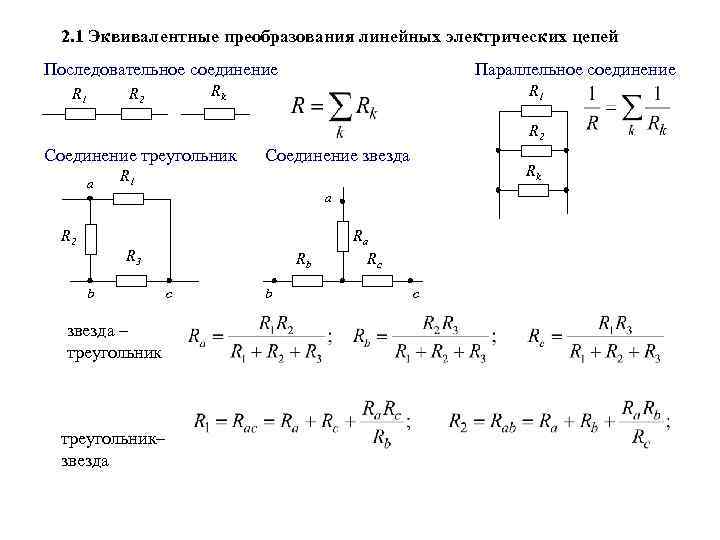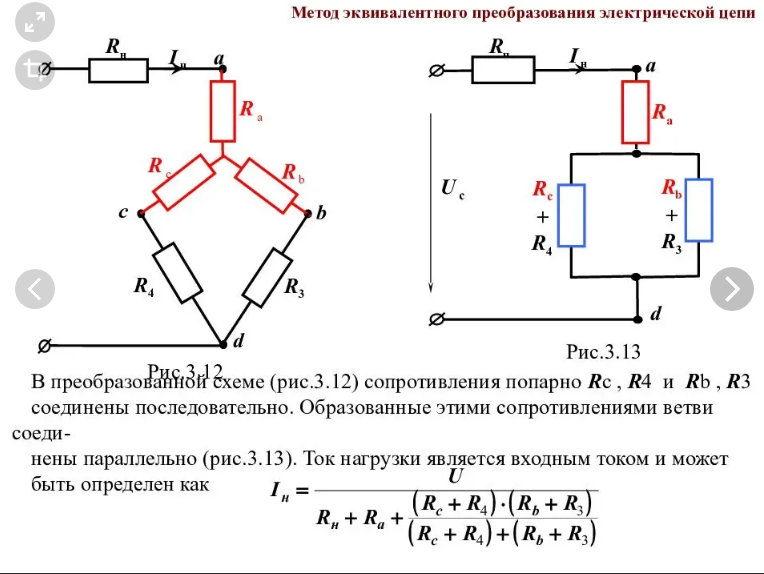
  

Метод эквивалентного преобразования схемы используют при расчете простых электрических цепей. В отдельных случаях имеется возможность применить его и для расчета сложных электрических цепей.

Суть метода эквивалентного преобразования схемы заключается в упрощении схемы, когда два (или несколько) однотипных элемента электрической цепи замещаются одним эквивалентным элементом того же типа. Под термином "эквивалентный элемент" подразумевается такой элемент, замещение на который не меняет значений токов и напряжений в остальной части электрической цепи.

Схематичный пример использования метода эквивалентного преобразования схемы для расчета сложной электрической цепи изображен ниже: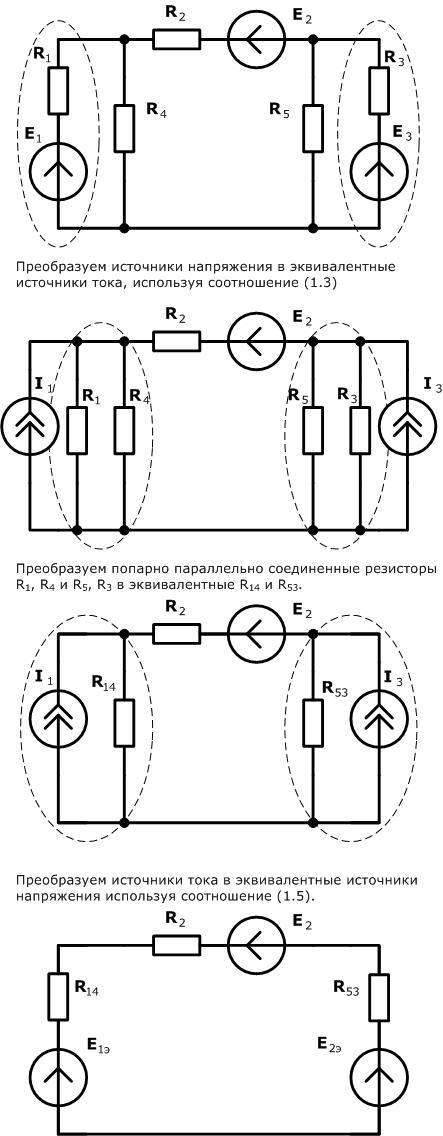


Например, после замены источника тока источником напряжения (рис. 1.3) в обобщенной ветви последняя будет выглядеть так:

	=
Рис.3.1		Рис.3.2

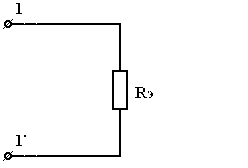
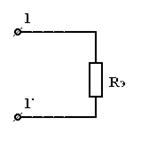
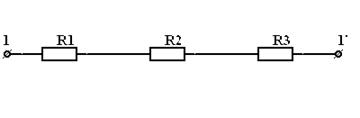
где   . Обратите внимание, направление эквивалентного источника ЭДС   совпадает с напряжением источника тока   . Ниже будет показано, что данный участок цепи можно упростить, как показано на рис. (3.2), где   .

3.2. Последовательное соединение резисторов при эквивалентной замене суммируется: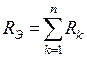

 ,

где   – число последовательно соединенных резисторов. При данном соединении   всегда больше большего из   сопротивлений. В частном случае, если каждое из   сопротивлений равно   , то   .

Пример. Определить эквивалентное сопротивление цепи на зажимах   .

a)

 .

	=
Рис 3.4		Рис 3.5

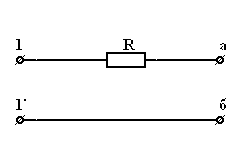
б)

	.
Рис 3.6

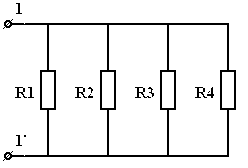
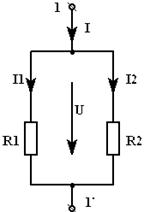
Здесь  , т.к. разрыв цепи между точками   и   имеет бесконечно большое сопротивление.

3.3. При параллельном соединении резистора суммируется их проводимость   , где   - число параллельно соединенных резисторов,   и  . При параллельном соединении   всегда меньше меньшего из   сопротивлений. В частном случае, если каждое из   сопротивлений равно   , то   . В случае двух параллельно соединенных сопротивлений   и   :

	=
Рис 3.7		Рис 3.8
,
	или	.

Пример. Определить   на зажимах   .

а)

	=
Рис 3.9		Рис 3.10

а)

 .

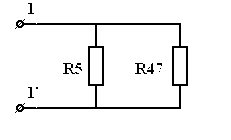
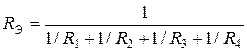б)

	.
Рис 3.10

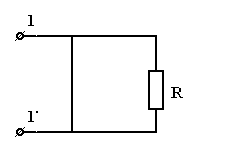
Здесь   , т.к. сопротивление закоротки равно нулю.

РАСЧЕТНЫЕ ФОРМУЛЫ

Тип элемента	Последовательное соединение m-элементов	Параллельное соединение m-элементов
Резисторы
Конденсаторы
Катушки индуктивности

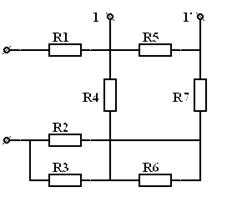
3.4. При смешанном соединении резисторов эквивалентное сопротивление   цепи определяет последовательным упрощением схемы и «сворачиванием» ее к одному сопротивлению, равному   . При расчете токов в отдельных ветвях ЭЦ «разворачивают» в обратной последовательности.

Пример. Определить   относительно зажимов   .

а)

	=		=
Рис 3.11		Рис 3.12		Рис 3.12

 , 

а)

.

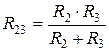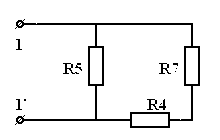
б)

	=		=
Рис 3.13		Рис 3.14		Рис 3.15

б)

 ,   .

	=
Рис 3.16		Рис 3.17
	=
Рис 3.18		Рис 3.19

в)

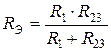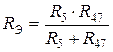 , где   .

• 
  5) энергетические соотношения в цепях постоянного тока
  
• 
  Для любой замкнутой электрической цепи должен соблюдаться баланс мощностей (энергетический баланс): алгебраическая сумма мощностей, развиваемых источниками электрической энергии, равна алгебраической сумме мощностей, расходуемых в приемниках энергии. При этом в качестве приемников электрической энергии необходимо учитывать как внешние сопротивлении (сопротивления нагрузки), так и внутренние сопротивления источников энергии.
  
• 
  Если направление ЭДС и тока   в источнике совпадают, их произведение при составлении баланса мощности записывается со знаком «+», если же их направления противоположны — со знаком «-».
  
• 
  Баланс мощности для схемы, приведенной на рис. 1.30 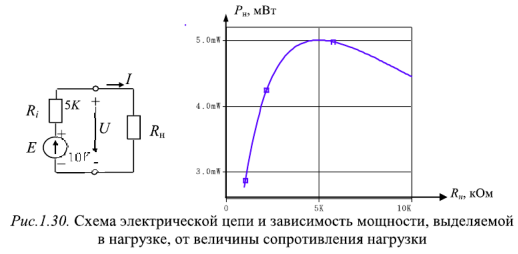 . Согласно этому уравнению, развиваемая источником мощность   состоит из потерь мощности на внутреннем сопротивлении источника   и мощности  , передаваемой источником вот внешнюю цепь.
  
• 
  
  
• 
  Ток   имеет максимальное значение при коротком замыкании   и равен пулю при холостом ходе  . Потери мощности на внутреннем сопротивлении источника максимальны при коротком замыкании.
  
• 
  Мощность, отдаваемая источником во внешнюю цепь, равна нулю, как при коротком замыкании, так и при холостом ходе. Она имеет максимальное значение, равное половине мощности развиваемой источником, когда сопротивление внешней цепи равно внутреннему сопротивлению источника (рис. 1.30), т.е. когда внешняя цепь источник работают в согласованном режиме.
  
• 
  Коэффициент полезного действия источника равен отношению мощности, расходуемой во внешней цепи, к мощности, развиваемой источником. В согласованном режиме он имеет максимальное значение и равен 0,5.
  

• 
  6) источник ЭДС напряжения и тока
  
• 
  В электротехнике пользуются понятиями источников ЭДС или напряжения и тока. При этом источником напряжения называется такой источник электроэнергии, у которого внутреннее сопротивление R₀ мало (С₀ - велика), поэтому напряжение на его зажимах практически не зависит от тока нагрузки; у источника тока R₀ велико (G₀ — мала), поэтому ток нагрузки практически не зависит от напряжения на его зажимах. Условные изображения реальных источников представлены на рис. 1.5, а, д.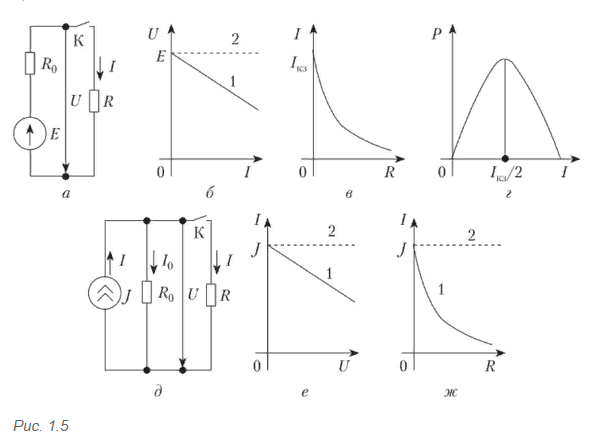
  
• 
  
  
• 
  Рис. 1.5
  
• 
  Важнейшей характеристикой источников напряжения и тока являются внешние характеристики, под которыми понимают: для источников ЭДС - зависимость напряжения от тока при постоянных ЭДС и внутреннем сопротивлении, снятые с использованием схемы по рис. 1.5, а (ключ К замкнут) т.е. U = F(I) при Е = const и R₀ = const; для источников тока — зависимость тока нагрузки от напряжения при постоянных токе источника и его внутренней проводимости, снятые с использованием схемы по рис. 1.5, д (ключ К замкнут), т.е. I = F(U) при J = const и G₀ = const. Практический интерес также представляют зависимости токов нагрузок от их сопротивлений, снятые с использованием схем по рис. 1.5, а и д (ключи К замкнуты) соответственно, т.е. I = F(R) при Е = const,/ = const, /?₀ = const.
  
• 
  Установим соотношения, описывающие указанные характеристики, и аппроксимируем (изобразим) их графически.
  
• 
  1. Реальными источниками ЭДС могут быть синхронные генераторы на электростанциях или аккумуляторные батареи, используемые во многих радиоэлектронных устройствах, мобильной технике (самолеты, автомобили, тракторы и др.). У них внутренние сопротивления малы.
  
• 
  Если но цепи, изображенной на рис. 1.5, а (ключ К замкнут), протекает ток /, то напряжение U на зажимах источника ЭДС будет равно ЭДС Е за вычетом падения напряжения на его внутреннем сопротивлении [/₀=/Д₀, т.е.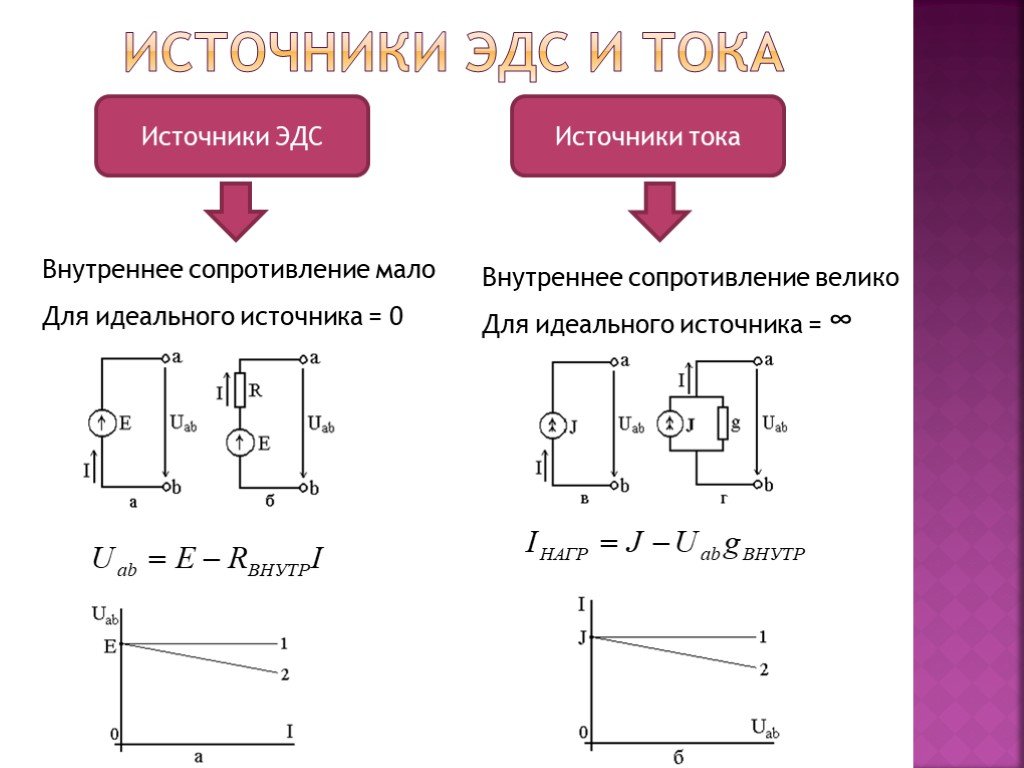
  
• 
  
  

• 
  7) последовательное соединение источников ЭДС
  

При последовательном соединении источников общая ЭДС равна алгебраиче-ской сумме ЭДС отдельных источников, общее внутреннее сопротивление рав-но сумме внутренних сопротивлений отдельных источников. Для определения знака ЭДС каждого источника нужно выбрать положительное направление движения на участке с этим источником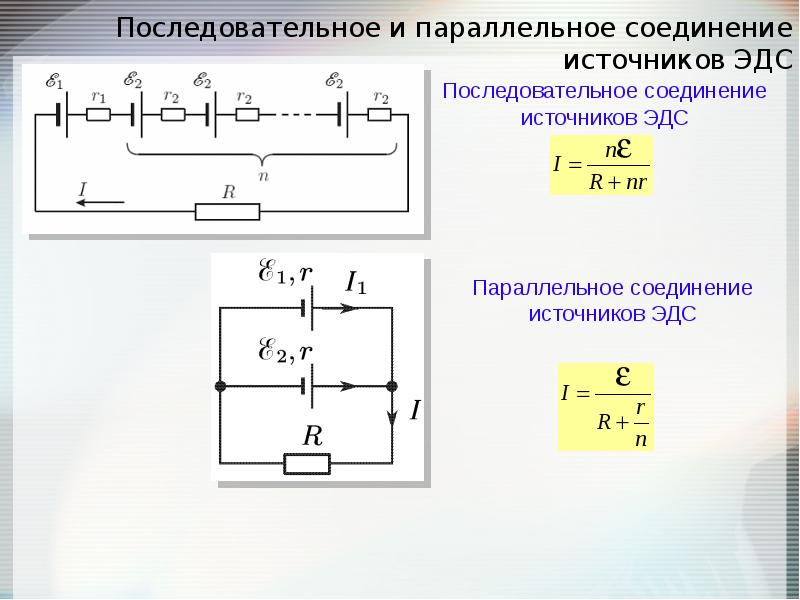

• 
  8) расчет цепей с помощью законов киркгофа
  

Принцип расчёта электрической цепи заключается в следующем:

Принимаем один из узлов цепи за базисный и присваиваем ему потенциал равный нулю

Для оставшихся узлов составляем уравнения по первому закону Кирхгофа, заменяя токи в ветвях по закону Ома через напряжение и сопротивление

После решения получившейся системы уравнений вычисляем токи в ветвях по обобщенному закону Ома




9)Метод контурных токов
Метод контурных токов:

Контурным током называют условный ток, протекающий внутри независимого контура.

Напомним, что контуры называются независимыми (подробнее см. разд. 2.1), если они отличаются друг от друга хотя бы одним элементом (ветвью). Направление отсчёта контурного тока выбирается произвольно и независимо от выбора направлений отсчётов контурных токов в других контурах. В отличие от метода токов ветвей, рассмотренного в лекции 4, данный метод позволяет уменьшить число уравнений, описывающих схему, до величины, равной числу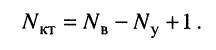 



Предварительно покажем, что при известных контурных токах можно найти токи всех ветвей, а потому и напряжения на всех элементах цепи. Действительно, ток в любом элементе (ветви) определяется по первому закону Кирхгофа (ЗТК) как алгебраическая сумма контурных токов, протекающих в этом элементе. Например, при выбранных в удлинителе (рис. 5.3) направлениях отсчётов токов элементов и контурных токов имеем: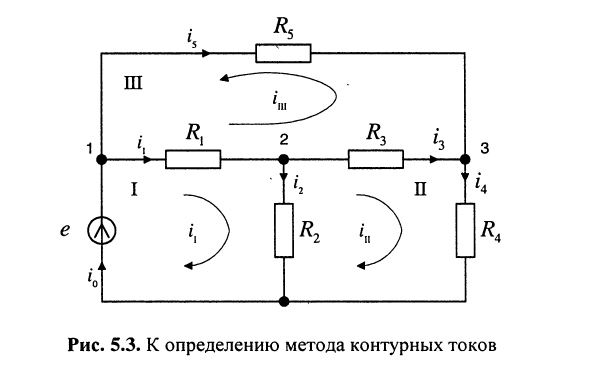





Зная токи, протекающие в элементах, можно по закону Ома определить напряжения на каждом из них.

Определение:

Метод анализа колебаний в электрических цепях, в котором неизвестными, подлежащими определению, являются контурные токи, называется методом контурных токов.

Составление контурных уравнений

При составлении системы контурных уравнений воспользуемся вторым законом Кирхгофа и будем полагать, что (рис. 5.4):

• 
  цепь согласно (5.4) содержит   независимых контуров;
  
• 
  в цепи имеются источники напряжения с ЭДС 
  
• 
  все   независимых контуров непосредственно связаны друг с другом, т. е. для к-го и 1-го контуров имеется хотя бы один                  элемент   который входит в оба эти контура, причём 
  

При этих условиях, выбранных независимых контурах и заданных направлениях отсчётов контурных токов запишем уравнение для первого контура (см. рис. 5.4) согласно второму закону Кирхгофа:

    (5.5)

Выразим напряжения на элементах 1-го контура через токи ветвей по закону Ома: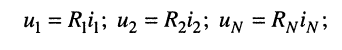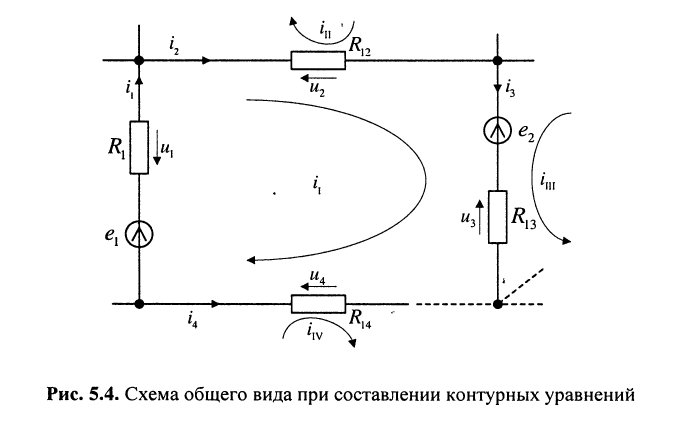





или в общем виде:

   (5.6)

• 
   — ток в  -ой ветви; 
  
• 
    — напряжение в  -ой ветви;
  
• 
     — сопротивление элемента, общего для 1-го и  -го контуров.
  

Подставим (5.6) в (5.5)

        (5.7)

и выразим токи ветвей через контурные токи, нумерация которых осуществляется римскими цифрами и прямыми латинскими буквами. Из рис. 5.4 видно, что: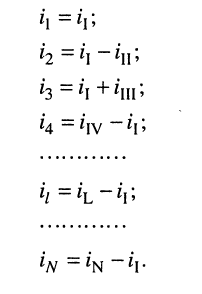



Произведём замену токов ветвей в выражении (5.7) через соотношения (5.8):



Умножим полученное уравнение на-1, раскроем скобки, приведём подобные члены и перенесём в правую часть известные значения напряжений источников; после выполнения этих действий контурное уравнение принимает вид



Подобное уравнение можно было бы составить и для любого другого контура, поэтому полученный результат позволяет сделать обобщающие выводы:

• 
  в левую часть каждого из уравнений входит N слагаемых, пропорциональных искомым контурным токам 
  
• 
  коэффициент при контурном токе  -го контура, для которого составляется уравнение, представляет собой арифметическую  сумму сопротивлений этого контура;
  
• 
  остальные слагаемые представляют собой произведение сопротивления элемента   общего для  -го и  -го контуров, на контурный ток 1-го контура; эти слагаемые входят в уравнение со знаком "+", если направления токов  -го и  -го контуров в элементе   совпадают; в противном случае они входят в уравнение с отрицательным знаком.
  

• 
  10) расчет цепей методом двух узлов
  

.

(это скорее всего не подходит)

• 
  11) параметры синусоидальных колебаний(векторная диаграмма) 
  

Теперь отложим вектор напряжения на катушке, масштаб для напряжения возьмем 5 В/см, получается, что нужно отложить шесть клеток вверх, так как напряжение в катушке опережает ток. Для наглядности обозначим синим цветом.

Далее мы будем откладывать вектор активного сопротивления, так как напряжение в одной фазе с током, то мы его откладываем из конца вектора U_L параллельно вектору тока I. Обозначим его красным цветом.

Следующим шагом отложим вектор напряжения на конденсаторе, так как оно запаздывает на 90°, мы его отложим вертикально вниз, из конца вектора U R . Обозначим желтым цветом.

И последним этапом мы отложим вектор общего напряжения, из начала координат в конец вектора U_C и обозначим его зеленым цветом.

Общее напряжение получилось равным 2,23 В, причем характер цепи емкостной, так как напряжение отстает от тока.

Аналогичным образом выполняется построение векторной диаграммы токов.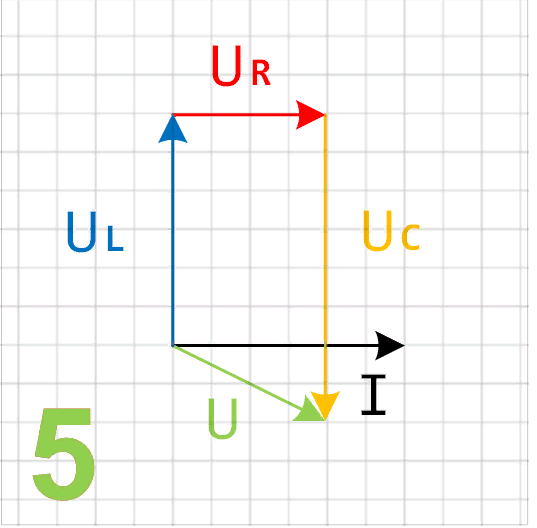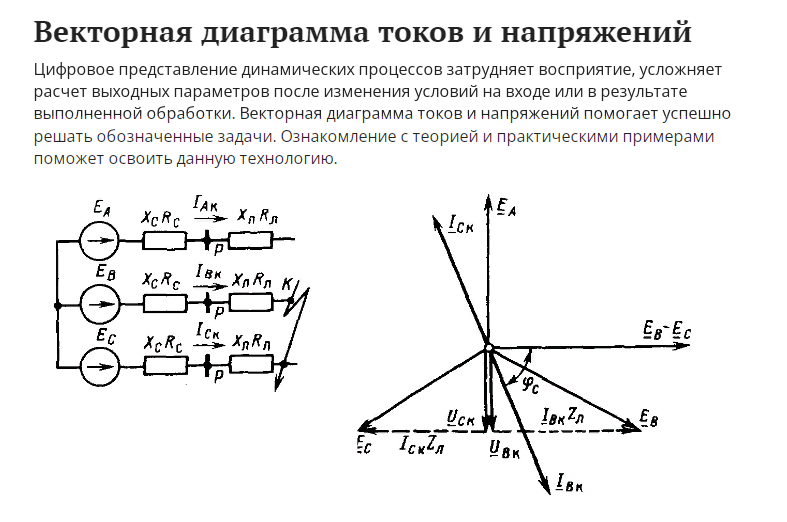
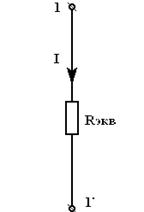
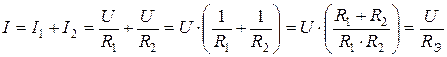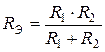
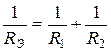