Электротехника ответы. Простейшая эл цепь и отношения в ней
 Скачать 5.18 Mb. Скачать 5.18 Mb.
|
Разновидности векторных диаграммДля корректного отображения переменных величин, которые определяют функциональность радиотехнических устройств, хорошо подходит векторная графика. Подразумевается соответствующее изменение основных параметров сигнала по стандартной синусоидальной (косинусоидальной) кривой. Для наглядного представления процесса гармоническое колебание представляют, как проекцию вектора на координатную ось. С применением типовых формул несложно рассчитать длину, которая получится равной амплитуде в определенный момент времени. Угол наклона будет показывать фазу. Суммарные влияния и соответствующие изменения векторов подчиняются обычным правилам геометрии. Различают качественные и точные диаграммы. Первые применяют для учета взаимных связей. Они помогают сделать предварительную оценку либо используются для полноценной замены вычислений. Другие создают с учетом полученных результатов, которые определяют размеры и направленность отдельных векторов. 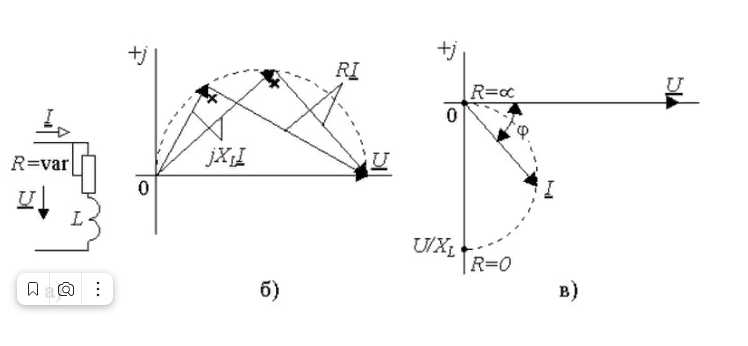  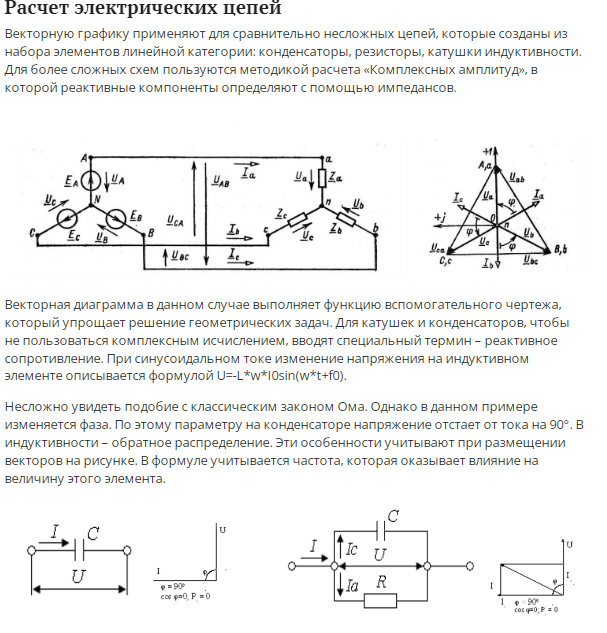 12)действующее значение переменных эдс и напряжения тока в цепи Мгновенное и максимальное значения. Величину переменной электродвижущей силы, силы тока, напряжения и мощности в любой момент времени называют мгновенными значениями этих величин и обозначают соответственно строчными буквами (e, i, u, p). Максимальным значением (амплитудой) переменной э. д. с. (или напряжения или тока) называется та наибольшая величина, которой она достигает за один период. Максимальное значение электродвижущей силы обозначается Еm, напряжения — Um, тока — Im. Действующим (или эффективным) значением переменного тока называется такая сила постоянного тока, которая, протекая через равное сопротивление и за одно и то же время, что и переменный ток, выделяет одинаковое количество тепла. Для синусоидального переменного тока действующее значение меньше максимального в 1,41 раз, т. е. в Аналогично действующие значения переменной электродвижущей силы и напряжения меньше их максимальных значений тоже в 1,41 раза. По величине измеренных действующих значений силы переменного тока, напряжения или электродвижущей силы можно вычислить их максимальные значения: Em = E · 1,41; Um = U · 1,41; Im = I · 1,41; Среднее значение= отношению количества эл энергии прошедшего через сечение проводника за половину периода к величине этого полупериода. Под средним значением понимают среднеарифметическое ее значение за половину периода. Источник Действующие значения тока и напряжения  Переменный синусоидальный ток в течение периода имеет различные мгновенные значения. Естественно поставить вопрос, какое же значение тока будет измеряться амперметром, включенным в цепь? Переменный синусоидальный ток в течение периода имеет различные мгновенные значения. Естественно поставить вопрос, какое же значение тока будет измеряться амперметром, включенным в цепь?При расчетах цепей переменного тока, а также при электрических измерениях неудобно пользоваться мгновенными или амплитудными значениями токов и напряжений, а их средние значения за период равны нулю. Кроме того, об электрическом эффекте периодически изменяющегося тока (о количестве выделенной теплоты, о совершенной работе и т. д.) нельзя судить по амплитуде этого тока. Наиболее удобным оказалось введение понятий так называемых действующих значений тока и напряжения . В основу этих понятий положено тепловое (или механическое) действие тока, не зависящее от его направления. Действующее значение переменного тока — это значение постоянного тока, при котором за период переменного тока в проводнике выделяется столько же теплоты, сколько и при переменном токе. Для оценки действия, производимого переменным током, мы сравним его действия с тепловым эффектом постоянного тока.  Мощность Р постоянного тока I , проходящего через сопротивление r , будет Р = Р 2 r . Мощность переменного тока выразится как средний эффект мгновенной мощности I 2 r за целый период или среднее значение от ( Im х sin ω t ) 2 х r за то же время. Пусть среднее значение t2 за период будет М. Приравнивая мощность постоянного тока и мощность при переменном токе, имеем: I 2 r = Mr, откуда I = √ M , Величина I называется действующим значением переменного тока. Среднее значение i2 при переменном токе определим следующим образом. Построим синусоидальную кривую изменения тока. Возведя в квадрат каждое мгновенное значение тока, получим кривую зависимости Р от времени. 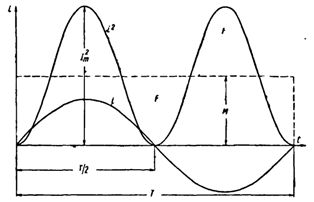 Обе половины этой кривой лежат выше горизонтальной оси, так как отрицательные значения тока (- i ) во второй половине периода, будучи возведены в квадрат, дают положительные величины. Построим прямоугольник с основанием Т и площадью, равной площади, ограниченной кривой i 2 и горизонтальной осью. Высота прямоугольника М будет соответствовать среднему значению Р за период. Это значение за период, вычисленное при помощи высшей математики, будет равно 1/2I 2 m . Следовательно, М = 1/2I 2 m Так как действующее значение I переменного тока равно I = √ M , то окончательно I = Im / √ 2 Аналогично зависимость между действующим и амплитудным значениями для напряжения U и Е имеет вид: U = Um / √ 2 E= Em / √ 2 Действующие значения переменных величин обозначаются прописными буквами без индексов ( I , U, Е). На основании сказанного выше можно сказать, что действующее значение переменного тока равно такому постоянному току, который, проходя через то же сопротивление, что и переменный ток, за то же время выделяет такое же количество энергии. 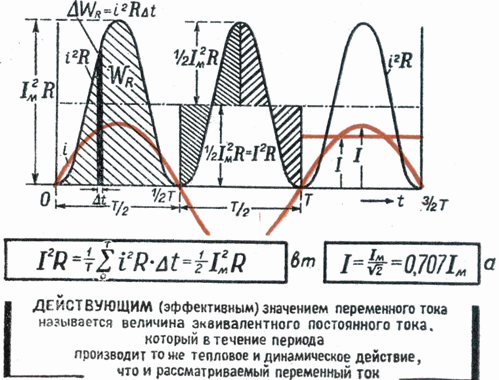 Электроизмерительные приборы (амперметры, вольтметры), включенные в цепь переменного тока, показывают действующие значения тока или напряжения.  13)Цепь переменного тока с активны сопротивлением и индуктивн 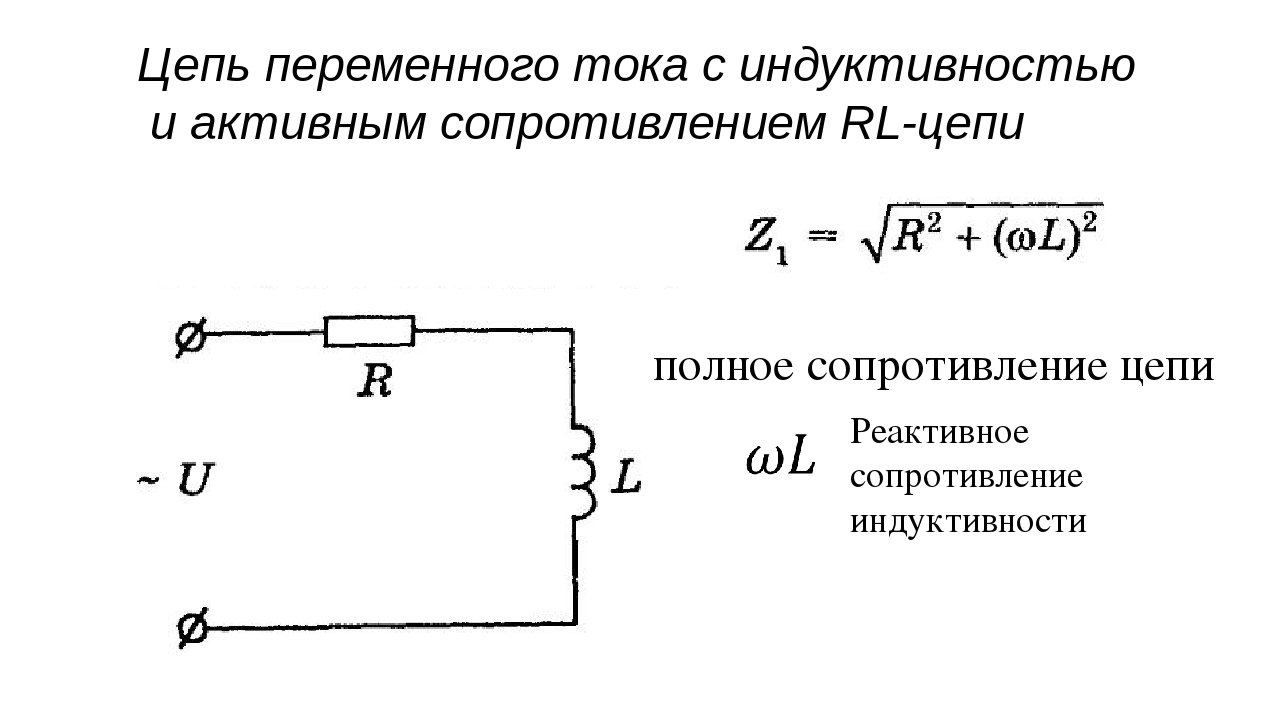 Рис.2.21 изображает неразветвлённую цепь с активным сопротивлением R и индуктивностью L. 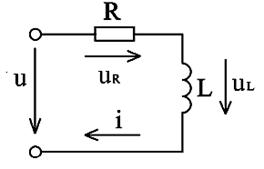 Рис.2.21. Цепь переменного тока с активным сопротивлением и индуктивностью Пусть мгновенный ток в цепи изменяется по закону . Тогда мгновенное напряжение на активном сопротивлении Построим для действующих значений напряжения и тока векторную диаграмму для рассматриваемой цепи (рис. 2.22). Векторы и образуют треугольник напряжений. Выведем закон Ома для этой цепи. Из треугольника напряжений имеем 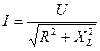 . (2.22) . (2.22)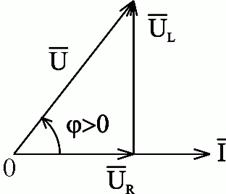 Рис.2.22. Векторная диаграмма действующих значений тока и напряжения цепи переменного тока с активным сопротивлением и индуктивностью Введем обозначение . (2.23) Полное сопротивление Z можно определить из треугольника сопротивлений (рис. 2.23). 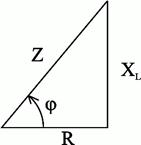 Рис.2.23. Треугольник сопротивлений цепи переменного тока с активным сопротивлением и индуктивностью Сдвиг фаз между током и напряжением определяется из треугольника сопротивлений: , (2.24) . (2.25) Поскольку вектор сдвинут по фазе относительно вектора на угол против часовой стрелки, этот угол имеет положительное значение. Если Таким образом, мгновенная мощность переменного тока может быть представлена в виде постоянной величины и, изменяющейся около неё с двойной частотой, величины Введем понятие средней или активной мощности: Активная мощность характеризует расход энергии на активном сопротивлении. Реактивная мощность характеризует обмен энергий между индуктивной катушкой и источником: Полная мощность оценивает предельную мощность нагрузки: 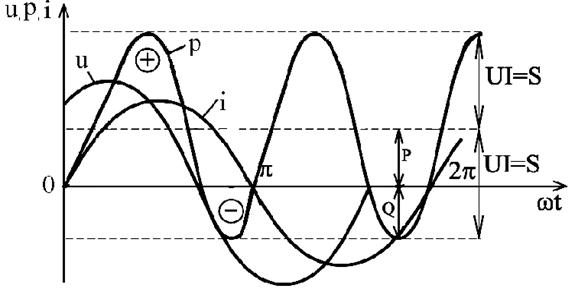 Рис.2.24. Зависимости мгновенных значений напряжения, тока и мощности цепи переменного тока с активным сопротивлением и индуктивностью Совокупность всех мощностей можно определить из треугольника мощностей (рис. 2.25). 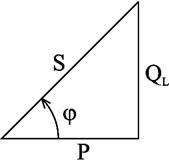 Рис.2.25. Треугольник мощностей Так: Коэффициент мощности cosφ изменяется от 0 до 1. По его величине судят, какую часть полной мощности составляет активная мощность. На практике стремятся к увеличению cosφ. 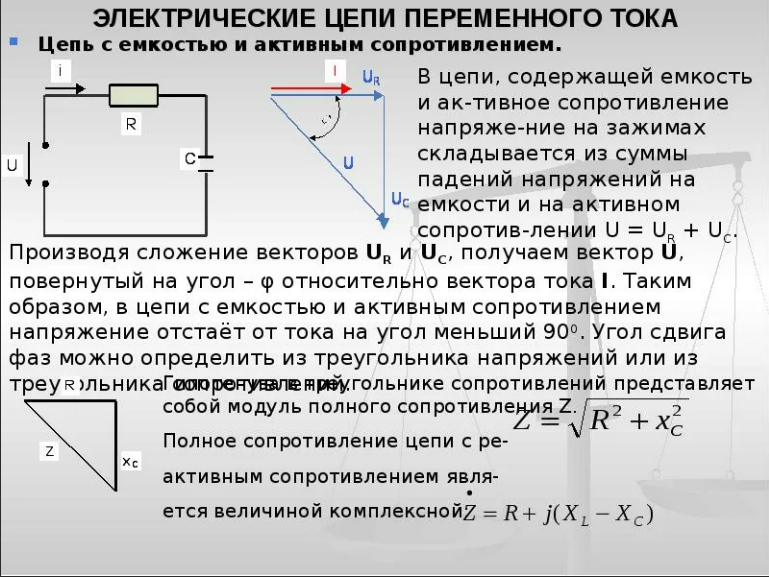 14) цепь с активным сопротивлениме и емкостью Цепь с ёмкостью – это электрическая цепь, состоящая из генератора переменного тока и идеального C – элемента - конденсатора. Условия идеальности цепи: · Ёмкость конденсатора не равна нулю, а его активное сопротивление и индуктивность равны нулю. 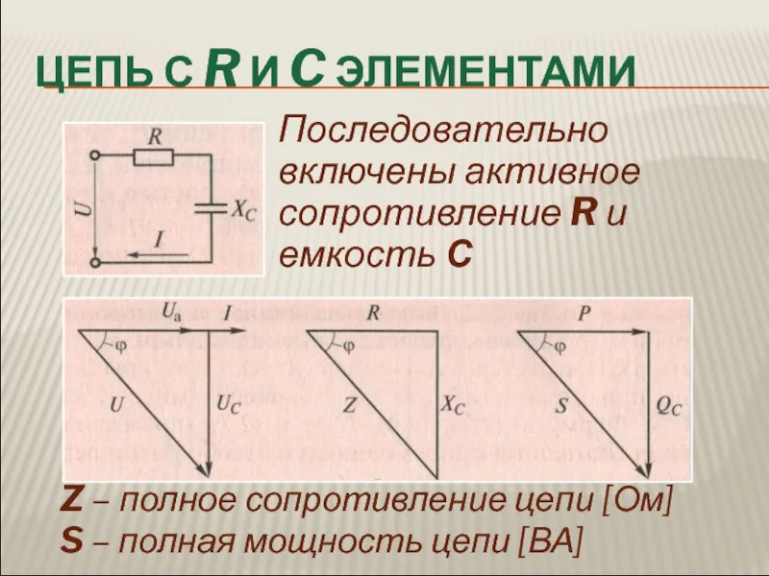 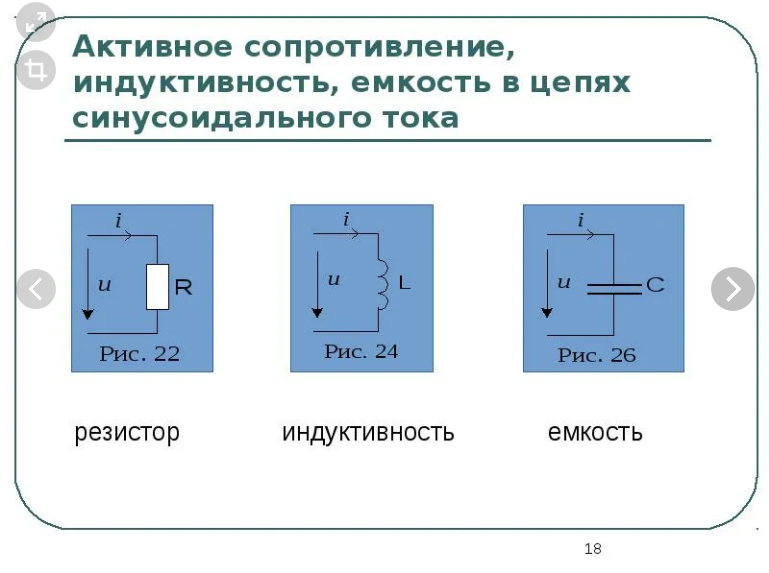 1.3. Цепь с активным сопротивлением, индуктивностью и емкостью 1.3. Цепь с активным сопротивлением, индуктивностью и емкостьюЦепь с R, L и С представляет собой общий случай последовательного соединения активных и реактивных сопротивлений и является последовательным колебательным контуром (рис. 5,а). Принимаем фазу тока нулевой: 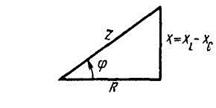 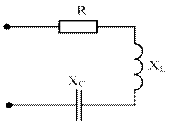 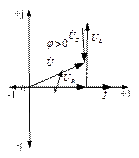 а) б) в) а) б) в)Рис. 5. Схема цепи переменного тока с R и L, ее векторная диаграмма, треугольник сопротивлений Тогда напряжение на активном сопротивлении Вектор результирующего напряжения U замыкает многоугольник векторов UR, ULи UС (рис. 5,б). Вектор UL+ Uc определяет напряжение на индуктивности и емкости. Как видно из диаграммы, это напряжение может быть меньше напряжения на каждом из участков в отдельности. Это объясняется процессом обмена энергией между индуктивностью и емкостью. Закон Ома для цепи с R, L и С. где – реактивное сопротивление цепи, Ом. При XL> Xc реактивное сопротивление положительно и сопротивление цепи носит активно-индуктивный характер, при XL< Xc реактивное сопротивление отрицательно и сопротивление цепи носит активно-емкостной характер. Таким образом, при XL≠XC преобладает или индуктивное, или емкостное сопротивление, т. е. с энергетической точки зрения цепь с R, L и С сводится к цепи с R, L или с R, С. Мощности: Знак сдвига фаз φ определяется по формуле |
