10781 ЗМУ Матем. Протокол от 05. 10. 2012 2 Председатель методической комиссии Маи ргппу а. В. Песков Директор Маи а. А. Жученко фгаоу впо Российский государственный профессионально педагогический университет
 Скачать 1.7 Mb. Скачать 1.7 Mb.
|
5. Неопределённый и определённый интегралы281-290. Найти неопределенные интегралы. В двух примерах (пункты а и б) проверить результаты дифференцированием. 281. а) 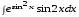 ; б) ; б) 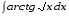 ; ;в) 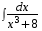 ; г) ; г) 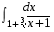 . .282. а) 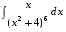 ; б) ; б) 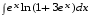 ; ;в) 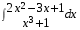 ; г) ; г) 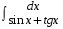 . .283. а) 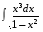 ; б) ; б) 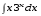 ; ;в) 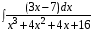 ; г) ; г) 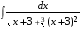 . .284. а) 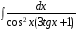 ; б) ; б) 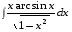 ; ;в) 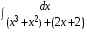 ; г) ; г) 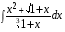 . .285. а) 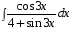 ; б) ; б) 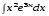 ; ;в) 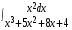 ; г) ; г) 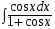 . .286. а) 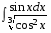 ; б) ; б) 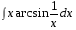 ; ;в) 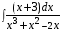 ; г) ; г) 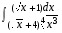 . .287. а) 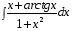 ; б) ; б) 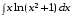 ; ;в) 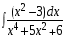 ; г) ; г) 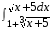 . .288. а) 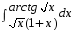 ; б) ; б) 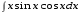 ; ;в) 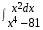 ; г) ; г) 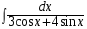 . .289. а) 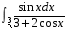 ; б) ; б) 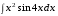 ; ;в) 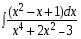 ; г) ; г) 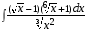 . .290. а) 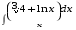 ; б) ; б) 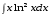 ; ;в) 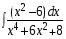 ; г) ; г) 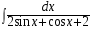 . .301-310. Вычислить несобственный интеграл или доказать его расходимость. 301. 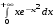 . 302. . 302. 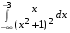 . .303. 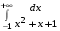 . 304. . 304. 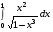 . .305. 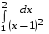 . 306. . 306. 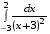 . .307. 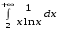 . . 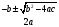 308. 308. 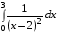 . .309. 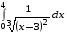 . 310. . 310. 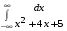 . . 6. Дифференциальные уравнения 321-330. Найти общее решение дифференциального уравнения. 321. 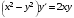 . 322. . 322. 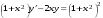 . .323. 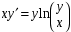 . 324. . 324. 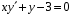 . .325. 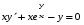 . 326. . 326. 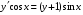 . .327. 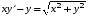 . 328. . 328. 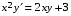 . .329. 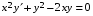 . 330. . 330. 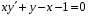 . .341-350. Найти частное решение дифференциального уравнения 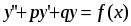 , удовлетворяющее начальным условиям , удовлетворяющее начальным условиям 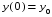 , , 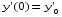 . .341. 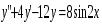 ; ; 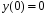 , , 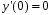 . .342. 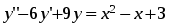 ; ; 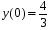 , , 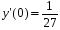 . .343. 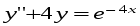 ; ; 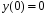 , , 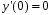 . .344. 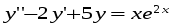 ; ; 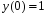 , , 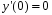 . .345. 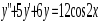 ; ; 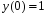 , , 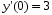 . .346. 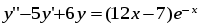 ; ; 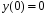 , , 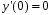 . .347. 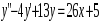 ; ; 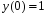 , , 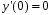 . .348. 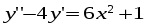 ; ; 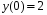 , , 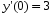 . .349. 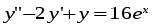 ; ; 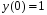 , , 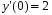 . .350. 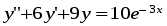 ; ; 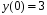 , , 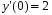 . .7. Двойные и криволинейные интегралы 351-360. Вычислить двойные интегралы по области D. 351. 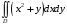 , где D – область, ограниченная линиям , где D – область, ограниченная линиям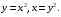 352. 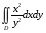 , где D – область, ограниченная линиями , где D – область, ограниченная линиями 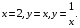 353. 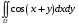 , где D – область, ограниченная линиями , где D – область, ограниченная линиями  354. 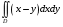 , где D – область, ограниченная линиями , где D – область, ограниченная линиями 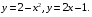 355. 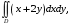 где D – область, ограниченная линиями где D – область, ограниченная линиями 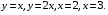 356. 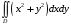 , где D – область, ограниченная линиями , где D – область, ограниченная линиями 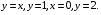 357. 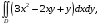 где D – область, ограниченная линиями где D – область, ограниченная линиями 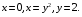 358. 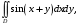 где D – область, ограниченная линиями где D – область, ограниченная линиями 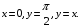 359. 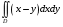 , где D – область, ограниченная линиями , где D – область, ограниченная линиями 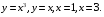 360. 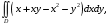 где D – область, ограниченная линиями где D – область, ограниченная линиями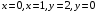 . . 361 – 370. Перейдя к полярным координатам, вычислить площадь фигуры, ограниченной областью D. 361. Область D ограниченна линиями: 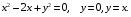 (І четв.) (І четв.)362. Область D ограниченна линиями: 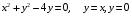 .(І четв.) .(І четв.)363. Область D ограниченна линиями: 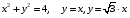 . (І четв.) . (І четв.)364. Область D ограниченна линиями: 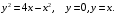 365. Область D ограниченна лемнискатой: 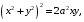 (І четв.) (І четв.)366. Область D ограниченна линиями: 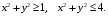 367. Область D ограниченна линиями: 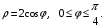 368. Область D ограниченна линиями: 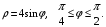 369. Область D ограниченна линиями: 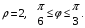 370. Область D ограниченна лемнискатой: 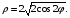 371 – 380. Вычислить криволинейные интегралы 371. 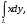 где L – контур треугольника, образованного осями координат и прямой где L – контур треугольника, образованного осями координат и прямой 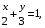 в положительном направлении, т.е. против движения часовой стрелки. в положительном направлении, т.е. против движения часовой стрелки.372. 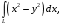 где L – дуга параболы где L – дуга параболы 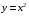 от точки О (0;0) до точки от точки О (0;0) до точки А(2;4). 373. 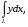 где L – контур прямоугольника, образованного прямыми где L – контур прямоугольника, образованного прямыми 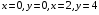 в положительном направлении (против часовой стрелки). в положительном направлении (против часовой стрелки).374. 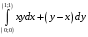 вдоль кривой вдоль кривой 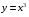 . .375. 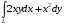 вдоль кривой вдоль кривой 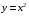 от точки О (0;0) до точки А(1;1). от точки О (0;0) до точки А(1;1).376. 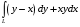 вдоль вдоль 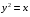 отточки О (0;0) до точки А(1;1). отточки О (0;0) до точки А(1;1).377. 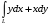 , где L – четверть окружности , где L – четверть окружности 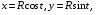 0 0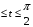 , против часовой стрелки. , против часовой стрелки.378. 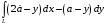 , где L – первая арка циклоиды , где L – первая арка циклоиды 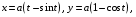 0 0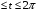 . .379. 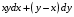 вдоль линии вдоль линии 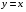 от точки О (0;0) до точки А(1;1). от точки О (0;0) до точки А(1;1).380. 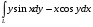 вдоль отрезка ОА, О (0;0), вдоль отрезка ОА, О (0;0), 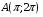 . . |
