Рабочая программа 10-11. РП 10-11 математика. Рабочая программа по математике (алгебра, геометрия) для 59 класса (базовый уровень), обучающегося по фгос ооо разработана на основе
 Скачать 88.84 Kb. Скачать 88.84 Kb.
|
|
МУНИЦИПАЛЬНОЕ АВТОНОМНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 8 ГОРОДСКОГО ОКРУГА ЩЕЛКОВО УТВЕРЖДЕНА приказом от 27.08.2021 № 121-ОД Рабочая программа по математике (алгебре, геометрии) на уровень среднего общего образования (базовый уровень) 10-11 классы Рабочая программа по математике (алгебра, геометрия) для 5-9 класса (базовый уровень), обучающегося по ФГОС ООО разработана на основе: - Положения « О рабочей программе учебных предметов, курсов», утвержденного приказом МБОУ СОШ №8 ЩМР МО, утверждённого приказом от 26.08.2021 № 120-ОД -Федерального государственного образовательного стандарта основного общего образования -Примерной ООП СОО по математике -Примерной программы воспитания - ООП СОО МАОУ СОШ № 8 ГОЩ Реализация учебной программы обеспечивается учебниками: 10 класс алгебра:Учебник для общеобразовательных учреждений: базовый и углубленный уровни/[Ю.М.Колягин, М.Ф.Ткачева, Н.Е.Федорова и др]. – 5-е изд. –М.: «Просвещение»,2018 г., геометрия: Геометрия, 10-11: учеб. для общеобразоват. учреждений: базовый и углубл. уровни / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – М.: Просвещение, 2018г. 11 класс алгебра:Учебник для общеобразовательных учреждений: базовый и углубленный уровни/[Ю.М.Колягин, М.Ф.Ткачева, Н.Е.Федорова и др]. – 5-е изд. –М.: «Просвещение»,2018 г., геометрия: Геометрия, 10-11: учеб. для общеобразоват. учреждений: базовый и углубл. уровни / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – М.: Просвещение, 2018г. Форма организации учебных занятий: классно-урочная. Формы промежуточной аттестации: Промежуточная аттестация в 10 классе будет проведена в форме итоговой контрольной работы в виде ЕГЭ (по алгебре и геометрии ) Промежуточная аттестация в 11 классе будет проведена в форме ЕГЭ (.Предмет математика (алгебра, геометрия) относится к предметной области Математика и информатика. Содержание учебного материала В соответствии с принятой Концепцией развития математического образования в Российской Федерации, математическое образование решает, в частности, следующие ключевые задачи: «предоставлять каждому обучающемуся возможность достижения уровня математических знаний, необходимого для дальнейшей успешной жизни в обществе»; «обеспечивать необходимое стране число выпускников, математическая подготовка которых достаточна для продолжения образования в различных направлениях и для практической деятельности, включая преподавание математики, математические исследования, работу в сфере информационных технологий и др.»; «в основном общем и среднем общем образовании необходимо предусмотреть подготовку обучающихся в соответствии с их запросами к уровню подготовки в сфере математического образования». Соответственно, выделяются три направления требований к результатам математического образования: практико-ориентированное математическое образование (математика для жизни); математика для использования в профессии; творческое направление, на которое нацелены те обучающиеся, которые планируют заниматься творческой и исследовательской работой в области математики, физики, экономики и других областях. Эти направления реализуются в двух блоках требований к результатам математического образования. На базовом уровне: Выпускник научится в 10–11-м классах: для использования в повседневной жизни и обеспечения возможности успешного продолжения образования по специальностям, не связанным с прикладным использованием математики. Выпускник получит возможность научиться в 10–11-м классах: для развития мышления, использования в повседневной жизни и обеспечения возможности успешного продолжения образования по специальностям, не связанным с прикладным использованием математики. На углубленном уровне: Выпускник научится в 10–11-м классах: для успешного продолжения образования по специальностям, связанным с прикладным использованием математики. Выпускник получит возможность научиться в 10–11-м классах: для обеспечения возможности успешного продолжения образования по специальностям, связанным с осуществлением научной и исследовательской деятельности в области математики и смежных наук. В соответствии с Федеральным законом «Об образовании в РФ» (ст. 12 п. 7) организации, осуществляющие образовательную деятельность, реализуют эти требования в образовательном процессе с учетом настоящей примерной основной образовательной программы Цели освоения программы базового уровня – обеспечение возможности использования математических знаний и умений в повседневной жизни и возможности успешного продолжения образования по специальностям, не связанным с прикладным использованием математики. Внутри этого уровня выделяются две различные программы: компенсирующая базовая и основная базовая. Компенсирующая базовая программа содержит расширенный блок повторения и предназначена для тех, кто по различным причинам после окончания основной школы не имеет достаточной подготовки для успешного освоения разделов алгебры и начал математического анализа, геометрии, статистики и теории вероятностей по программе средней (полной) общеобразовательной школы. Программа по математике на базовом уровне предназначена для обучающихся средней школы, не испытывавших серьезных затруднений на предыдущего уровня обучения. Обучающиеся, осуществляющие обучение на базовом уровне, должны освоить общие математические умения, необходимые для жизни в современном обществе; вместе с тем они получают возможность изучить предмет глубже, с тем чтобы в дальнейшем при необходимости изучать математику для профессионального применения. При изучении математики на углубленном уроне предъявляются требования, соответствующие направлению «математика для профессиональной деятельности»; вместе с тем выпускник получает возможность изучить математику на гораздо более высоком уровне, что создаст фундамент для дальнейшего серьезного изучения математики в вузе. Примерные программы содержат сравнительно новый для российской школы раздел «Вероятность и статистика». К этому разделу относятся также сведения из логики, комбинаторики и теории графов, значительно варьирующиеся в зависимости от типа программы. Во всех примерных программах большое внимание уделяется практико-ориентированным задачам. Одна из основных целей, которую разработчики ставили перед собой, – создать примерные программы, где есть место применению математических знаний в жизни. При изучении математики большое внимание уделяется развитию коммуникативных умений (формулировать, аргументировать и критиковать), формированию основ логического мышления в части проверки истинности и ложности утверждений, построения примеров и контрпримеров, цепочек утверждений, формулировки отрицаний, а также необходимых и достаточных условий. В зависимости от уровня программы больше или меньше внимания уделяется умению работать по алгоритму, методам поиска алгоритма и определению границ применимости алгоритмов. Требования, сформулированные в разделе «Геометрия», в большей степени относятся к развитию пространственных представлений и графических методов, чем к формальному описанию стереометрических фактов. Базовый уровень Компенсирующая базовая программа Алгебра и начала математического анализа Натуральные числа, запись, разрядные слагаемые, арифметические действия. Числа и десятичная система счисления. Натуральные числа, делимость, признаки делимости на 2, 3, 4, 5, 9, 10. Разложение числа на множители. Остатки. Решение арифметических задач практического содержания. Целые числа. Модуль числа и его свойства. Части и доли. Дроби и действия с дробями. Округление, приближение. Решение практических задач на прикидку и оценку. Проценты. Решение задач практического содержания на части и проценты. Степень с натуральным и целым показателем. Свойства степеней. Стандартный вид числа. Алгебраические выражения. Значение алгебраического выражения. Квадратный корень. Изображение числа на числовой прямой. Приближенное значение иррациональных чисел. Понятие многочлена. Разложение многочлена на множители, Уравнение, корень уравнения. Линейные, квадратные уравнения и системы линейных уравнений. Решение простейших задач на движение, совместную работу, проценты. Числовые неравенства и их свойства. Линейные неравенства с одной переменной и их системы. Числовые промежутки. Объединение и пересечение промежутков. Зависимость величин, функция, аргумент и значение, основные свойства функций. График функции. Линейная функция. Ее график. Угловой коэффициент прямой. Квадратичная функция. График и свойства квадратичной функции. график функции 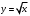 . График функции . График функции 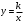 . . Нули функции, промежутки знакопостоянства, монотонность (возрастание или убывание) на числовом промежутке. Наибольшее и наименьшее значение функции. Периодические функции и наименьший период. Градусная мера угла. Тригонометрическая окружность. Определение синуса, косинуса, тангенса произвольного угла. Основное тригонометрическое тождество. Значения тригонометрических функций для углов 0, 30, 45, 60, 90, 180, 270. Графики тригонометрических функций 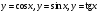 . .Решение простейших тригонометрических уравнений с помощью тригонометрической окружности. Понятие степени с действительным показателем. Простейшие показательные уравнения и неравенства. Показательная функция и ее график. Логарифм числа, основные свойства логарифма. Десятичный логарифм. Простейшие логарифмические уравнения и неравенства. Логарифмическая функция и ее график. Понятие степенной функции и ее график. Простейшие иррациональные уравнения. Касательная к графику функции. Понятие производной функции в точке как тангенс угла наклона касательной. Геометрический и физический смысл производной. Производные многочленов. Точки экстремума (максимума и минимума). Исследование элементарных функций на точки экстремума с помощью производной. Наглядная интерпретация. Понятие первообразной функции. Физический смысл первообразной. Понятие об интеграле как площади под графиком функции. Геометрия Фигуры на плоскости и в пространстве. Длина и площадь. Периметры и площади фигур. Параллельность и перпендикулярность прямых и плоскостей. Треугольники. Виды треугольников: остроугольные, тупоугольные, прямоугольные. Катет против угла в 30 градусов. Внешний угол треугольника. Биссектриса, медиана и высота треугольника. Равенство треугольников. Решение задач на клетчатой бумаге. Равнобедренный треугольник, равносторонний треугольник. Свойства равнобедренного треугольника. Соотношения между сторонами и углами в прямоугольном треугольнике. Тригонометрические функции углов в прямоугольном треугольнике. Теорема Пифагора. Применение теорем синусов и косинусов. Четырехугольники: параллелограмм, ромб, прямоугольник, квадрат, трапеция и их свойства. Средняя линия треугольника и трапеции. Выпуклые и невыпуклые фигуры. Периметр многоугольника. Правильный многоугольник. Углы на плоскости и в пространстве. Вертикальные и смежные углы. Сумма внутренних углов треугольника и четырехугольника. Соотношения в квадрате и равностороннем треугольнике. Диагонали многоугольника. Подобные треугольники в простейших случаях. Формулы площади прямоугольника, треугольника, ромба, трапеции. Окружность и круг. Радиус и диаметр. Длина окружности и площадь круга. Число . Вписанный угол, в частности угол, опирающийся на диаметр. Касательная к окружности и ее свойство. Куб. Соотношения в кубе. Тетраэдр, правильный тетраэдр. Правильная пирамида и призма. Прямая призма. Изображение некоторых многогранников на плоскости. Прямоугольный параллелепипед. Теорема Пифагора в пространстве. Задачи на вычисление расстояний в пространстве с помощью теоремы Пифагора. Развертка прямоугольного параллелепипеда. Конус, цилиндр, шар и сфера. Проекции фигур на плоскость. Изображение цилиндра, конуса и сферы на плоскости. Понятие об объемах тел. Использование для решения задач на нахождение геометрических величин формул объема призмы, цилиндра, пирамиды, конуса, шара. Понятие о подобии на плоскости и в пространстве. Отношение площадей и объемов подобных фигур. Вероятность и статистика. Логика и комбинаторика Логика. Верные и неверные утверждения. Следствие. Контрпример. Множество. Перебор вариантов. Таблицы. Столбчатые и круговые диаграммы. Числовые наборы. Среднее арифметическое, медиана, наибольшее и наименьшее значения. Примеры изменчивых величин. Частота и вероятность события. Случайный выбор. Вычисление вероятностей событий в опытах с равновозможными элементарными событиями. Независимые события. Формула сложения вероятностей. Примеры случайных величин. Равномерное распределение. Примеры нормального распределения в природе. Понятие о законе больших чисел. Основная базовая программа Алгебра и начала анализа Повторение. Решение задач с использованием свойств чисел и систем счисления, делимости, долей и частей, процентов, модулей чисел. Решение задач с использованием свойств степеней и корней, многочленов, преобразований многочленов и дробно-рациональных выражений. Решение задач с использованием градусной меры угла. Модуль числа и его свойства. Решение задач на движение и совместную работу с помощью линейных и квадратных уравнений и их систем. Решение задач с помощью числовых неравенств и систем неравенств с одной переменной, с применением изображения числовых промежутков. Решение задач с использованием числовых функций и их графиков. Использование свойств и графиков линейных и квадратичных функций, обратной пропорциональности и функции 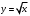 . Графическое решение уравнений и неравенств. . Графическое решение уравнений и неравенств.Тригонометрическая окружность, радианная мера угла. Синус, косинус, тангенс, котангенс произвольного угла. Основное тригонометрическое тождество и следствия из него. Значения тригонометрических функций для углов 0, 30, 45, 60, 90, 180, 270. ( 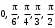 рад). Формулы сложения тригонометрических функций, формулы приведения, формулы двойного аргумента.. рад). Формулы сложения тригонометрических функций, формулы приведения, формулы двойного аргумента.. Нули функции, промежутки знакопостоянства, монотонность. Наибольшее и наименьшее значение функции. Периодические функции. Четность и нечетность функций. Сложные функции. Тригонометрические функции 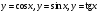 . Функция . Функция  . Свойства и графики тригонометрических функций. . Свойства и графики тригонометрических функций.Арккосинус, арксинус, арктангенс числа. Арккотангенс числа. Простейшие тригонометрические уравнения. Решение тригонометрических уравнений. Обратные тригонометрические функции, их свойства и графики. Решение простейших тригонометрических неравенств. Степень с действительным показателем, свойства степени. Простейшие показательные уравнения и неравенства. Показательная функция и ее свойства и график. Логарифм числа, свойства логарифма. Десятичный логарифм. Число е. Натуральный логарифм. Преобразование логарифмических выражений. Логарифмические уравнения и неравенства. Логарифмическая функция и ее свойства и график. Степенная функция и ее свойства и график. Иррациональные уравнения. Метод интервалов для решения неравенств. Преобразования графиков функций: сдвиг вдоль координатных осей, растяжение и сжатие, отражение относительно координатных осей. Графические методы решения уравнений и неравенств. Решение уравнений и неравенств, содержащих переменную под знаком модуля. Системы показательных, логарифмических и иррациональных уравнений. Системы показательных, логарифмических неравенств. Взаимно обратные функции. Графики взаимно обратных функций. Уравнения, системы уравнений с параметром. Производная функции в точке. Касательная к графику функции. Геометрический и физический смысл производной. Производные элементарных функций. Правила дифференцирования. Вторая производная, ее геометрический и физический смысл. Понятие о непрерывных функциях. Точки экстремума (максимума и минимума). Исследование элементарных функций на точки экстремума, наибольшее и наименьшее значение с помощью производной. Построение графиков функций с помощью производных. Применение производной при решении задач. Первообразная. Первообразные элементарных функций. Площадь криволинейной трапеции. Формула Ньютона-Лейбница. Определенный интеграл. Вычисление площадей плоских фигур и объемов тел вращения с помощью интеграла. |
