ОУД.08 Практика. Работа с программным обеспечением пк обучающихся
 Скачать 6.69 Mb. Скачать 6.69 Mb.
|
|
Тема: Представление информации в различных системах счисления Цель: освоить алгоритмы перевода числа из одной системы счисления в другую, познакомиться с действиями перехода между системами счисления с основаниями 2, 8, 16. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 1. Изучите краткие теоретические сведения. Рассмотрите примеры решения заданий. Системы счисления, используемые в компьютерах Двоичная система счисления. Для записи чисел используются только две цифры – 0 и 1. Выбор двоичной системы объясняется тем, что электронные элементы, из которых строятся ЭВМ, могут находиться только в двух хорошо различимых состояниях. По существу эти элементы представляют собой выключатели. Как известно выключатель либо включен, либо выключен. Третьего не дано. Одно из состояний обозначается цифрой 1, другое – 0. Благодаря таким особенностям двоичная система стала стандартом при построении ЭВМ. Восьмеричная система счисления. Для записи чисел используется восемь чисел 0,1,2,3,4,5,6,7. Шестнадцатеричная система счисления. Для записи чисел в шестнадцатеричной системе необходимо располагать шестнадцатью символами, используемыми как цифры. В качестве первых десяти используются те же, что и в десятичной системе. Для обозначения остальных шести цифр (в десятичной они соответствуют числам 10,11,12,13,14,15) используются буквы латинского алфавита – A,B,C,D,E,F. Перевод чисел из одной системы счисления в другую. Правилоперевода целых чисел из десятичной системы счисления в систему с основанием q: Последовательно выполнять деление исходного числа и получаемых частных на q до тех пор, пока не получим частное, меньшее делителя. Полученные при таком делении остатки – цифры числа в системе счисления q – записать в обратном порядке (снизу вверх). Пример 1. Перевести 2610 в двоичную систему счисления. А10->А2 Решение: 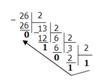 Ответ: 2610=110102 Пример 2. Перевести 1910 в троичную систему счисления. А10->А3. Решение: 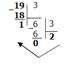 Ответ: 1910=2013. Пример 3. Перевести 24110 в восьмеричную систему счисления. А10->А8 Решение: 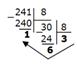 Ответ: 24110=3618. Пример4. Перевести 362710 в шестнадцатеричную систему счисления. А10->А16 Решение: 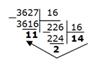 Т.к. в шестнадцатеричной системе счисления 14 – Е, а 11 – В, то получаем ответ Е2В16. Ответ: 362710=E2B16. Перевод чисел из любой системы счисления в десятичную. Правило: Для того чтобы число из любой системы счисления перевести в десятичную систему счисления, необходимо его представить в развернутом виде и произвести вычисления. Пример 5. Перевести число 1101102 из двоичной системы счисления в десятичную. Решение: 1101102 = 1*25 + 1*24 + 0*23+1*22+1*21+0*20=32+16+4+2=5410. Ответ: 1101102 = 5410. Пример 6. Перевести число 101,012 из двоичной системы счисления в десятичную. Решение: 101,012 = 1*22 + 0*21 + 1*20+0*2-1+1*2-2 =4+0+1+0+0,25=5,2510. Ответ: 101,012 = 5,2510. Пример 7. Перевести число 1221003 из троичной системы счисления в десятичную. Решение: 122013=1*34 + 2*33 + 2*32 + 0*31 + 1*30 = 81+54+18+1 = 15410. Ответ: 122013 = 15410. Пример 8. Перевести число 1637 из семеричной системы счисления в десятичную. Решение: 1637 = 1*72 + 6*71 + 3*70 = 49+42+3= 9410. Ответ: 1637 = 9410. Пример 9. Перевести число 2Е16 в десятичную систему счисления. Решение: 2Е16 = 2*161 +14*160 = 32 +14 = 4610. Ответ: 2Е16 = 4610. Перевод чисел из двоичной системы счисления в восьмеричную и шестнадцатеричную системы счисления Перевод целых чисел. Правило: Чтобы перевести целое двоичное число в восьмеричную (8=23) систему счисления необходимо: разбить данное число справа налево на группы по 3 цифры в каждой (триады); рассмотреть каждую триаду и записать ее соответствующей цифрой восьмеричной системы счисления, согласно таблице1. Таблица1
Пример 10. Перевести число 111010102 в восьмеричную систему счисления. Решение: 11 101 010 3 5 2 Ответ: 111010102 = 3528 . Пример 11. Перевести число 111100000101102 в восьмеричную систему счисления. Решение: 111 110 000 010 110 7 6 0 2 6 Ответ: 111100000101102= 760268. Правило:Чтобы перевести целое двоичное число в шестнадцатеричную (16=24) систему счисления необходимо: разбить данное число справа налево на группы по 4 цифры в каждой (тетрады); рассмотреть каждую тетраду и записать ее соответствующей цифрой шестнадцатеричной системы счисления, согласно таблице2: Таблица2
Пример 12. Перевести число 111000102 в шестнадцатеричную систему счисления. Решение: 1110 0010 Е 2 Ответ: 111000102 = Е216 . Перевод чисел из восьмеричной и шестнадцатеричной систем счисления в двоичную систему счисления. Правило: Для того, чтобы восьмеричное (шестнадцатеричное) число перевести в двоичную систему счисления, необходимо каждую цифру этого числа заменить соответствующим числом, состоящим из 3 (4) цифр двоичной системы счисления, согласно таблиц 1 и 2. Пример 13. Перевести число 5238 перевести в двоичную систему счисления. Решение: 5 2 3 101 010 011 Ответ: 5238 = 1010100112. Пример 14. Перевести число 4ВА3516 перевести в двоичную систему счисления. Решение: 4 В А 3 5 100 1011 1010 0011 0101 Ответ: 4ВА3516 = 100 1011 1010 0011 01012. 2. Практическая часть. Задания Задание 1. Переведите в десятичную систему счисления следующие числа из … системы счисления.
Задание 2. Переведите десятичные числа в заданные системы счисления.
Задание 3. Преобразуйте двоичные числа в восьмеричные и шестнадцатеричные.
Задание 4. Переведите в двоичную систему десятичные числа.
3. Содержание отчета. Отчет должен содержать: Название работы. Цель работы. Задания 1-4 и их решение. Вывод по работе. 4. Контрольные вопросы Что такое система счисления? Что такое основание системы счисления? Что такое непозиционная система счисления? Что такое позиционная система счисления? Из каких знаков состоит алфавит десятичной и двоичной систем? Почему в вычислительной технике взята за основу двоичная система счисления? Какое наибольшее десятичное число можно записать тремя цифрами: в двоичной системе; в восьмеричной системе; в шестнадцатеричной системе? Практическая работа №5 |
