РТЦиС_метода к лабам. Радиотехнические цепи и сигналы лабораторный практикум
 Скачать 1.84 Mb.
|
Содержание отчетаОтчет должен содержать краткие теоретические сведения об анализе преобразования радиосигналов избирательными цепями с использованием метода низкочастотного эквивалента и комплексной огибающей. Необходимо привести схему фильтра на основе одиночного параллельного колебательного контура, описать его характеристики и характеристики соответствующего низкочастотного эквивалента; привести схему лабораторного макета и структурную схему лабораторной установки. Отчет должен содержать следующие материалы экспериментальных исследований (с кратким пояснением вида зависимостей):
Контрольные вопросы
6. ПРЕОБРАЗОВАНИЕ СЛУЧАЙНЫХ ПРОЦЕССОВ В ЛИНЕЙНЫХ ЦЕПЯХЦель работы — изучение частотных и временных характеристик случайных процессов, их взаимосвязи и преобразования при прохождении через линейную цепь. 6.1. Теоретические сведенияВероятностные характеристики случайных процессов. Случайными называют сигналы, мгновенные значения которых заранее неизвестны и могут быть предсказаны лишь с некоторой вероятностью, меньшей единицы. Их характеристики могут быть только статистическими, т. е. иметь вероятностный вид. В радиоэлектронике все сигналы, несущие информацию, а также большинство помех и шум являются случайными. По отношению к случайной величине, изменяющейся во времени, например мгновенному значению напряжения случайного сигнала u(t), применяют термин случайный процесс. Этот термин объединяет случайные сигналы, помехи и шумы. Конкретный вид части случайного процесса на ограниченном интервале времени (например, в виде записи в запоминающем осциллографе) называют его реализацией. Большинство случайных процессов, встречающихся на практике, с достаточной точностью можно считать стационарными и эргодическими. Случайный процесс называется стационарным в широком смысле, если его двухмерная плотность вероятности удовлетворяет условию  , где  При этом одномерная плотность вероятности от времени не зависит:  Случайный процесс называется эргодическим, если любая его характеристика, полученная статистическим усреднением по множеству реализаций, совпадает с такой же характеристикой, полученной усреднением по времени одной реализации достаточно большой длины. Отклонения случайного процесса u(t) от его среднего значения 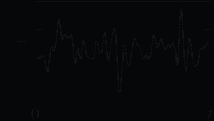 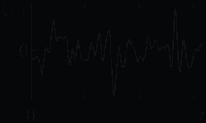(постоянной составляющей, рис. 6.1, а) называют флуктуациями (рис. 6.1, б) . (6.1)  а б Рис. 6.1 При исследовании стационарных эргодических процессов основной интерес представляют свойства их флуктуаций (t), для описания которых вводят корреляционную функцию (КФ) флуктуаций и спектральную плотность мощности. Корреляционно-спектральный анализ случайных процессов. Корреляционная функция R() является мерой статистической связи между мгновенными значениями случайного процесса, разделенными интервалом времени . Иными словами, она позволяет оценить, насколько существенно в среднем успеет измениться значение флуктуаций за время по сравнению с наблюдаемым мгновенным значением в исходный момент времени t. Для стационарного эргодического процесса КФ определяется соотношением  , (6.2)где (t) и (t + ) — мгновенные значения флуктуаций соответственно в моменты t и t + ; 2Т — длина реализации, на которой производится усреднение. Знак может быть любым. Чтобы лучше уяснить физический смысл этого выражения, рассмотрим следующую операцию предельного перехода. Возьмем реализацию случайного процесса (рис. 6.2) длиной 2Т и выберем на ней отсчетные моменты времени  , …, следующие с равным шагом. Зададимся интервалом времени и определим мгновенные значения:  ,  ;  ,  ;  ,  и т. д. Затем вычислим сумму (6.3)и разделим ее на длину реализации 2Т (в этом и заключается операция усреднения). Чтобы перейти к определению (6.2), надо брать моменты 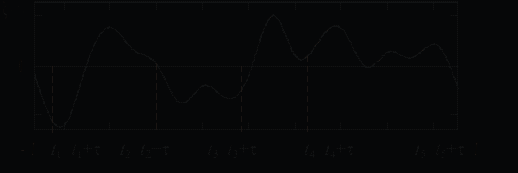 с бесконечно малым шагом dt, а длину реализации 2Т устремить к бесконечности. В результате получим одно значение КФ для выбранного значения . Если процесс во времени изменяется медленно, то за интервал его мгновенные значения существенно не изменятся (как, например, на рис. 6.2).  Рис. 6.2 Поэтому с большой вероятностью сомножители  ,  в сумме (6.3) окажутся с одним знаком; большинство слагаемых будут положительными и в результате вычисленное значение R() окажется существенно больше нуля.При более быстром изменении значений процесса во времени или при значительном увеличении интервала статистическая связь между значениями и ослабевает, их знаки с равной вероятностью могут оказаться как одинаковыми, так и разными. В результате сумма (6.3) и значение R() стремятся к нулю.Функция R() достигает максимума при = 0. Значение R(0) R() соответствует средней мощности флуктуаций (дисперсии):  .Чтобы располагать характеристикой временных свойств процесса, не зависящей от его мощности, КФ нормируют: r() = R()/R(0), (6.4) где r() — коэффициент корреляции, или нормированная КФ. Его основные свойства: r(0) = 1; r(–) = r(); |r()| r(0); r( . (6.5) Подчеркнем четность функций R() = R(–) и r() = r(–). Конкретный вид R() и r() однозначно определяется свойствами рассматриваемого случайного процесса, но с увеличением || обе функции стремятся к нулю, хотя и не всегда монотонно (например, в виде затухающих колебаний). Спектральная плотность мощности (СПМ) флуктуаций случайного процесса есть функция W, описывающая распределение средней мощности флуктуаций по частоте. Физический смысл СПМ состоит в следующем: W представляет собой среднюю мощность флуктуаций, приходящуюся на полосу частот 1 рад/с (или 1/(2) Гц) при заданной частоте = 2f. Формально W определяют, усредняя квадраты модулей спектральных плотностей напряжения большого числа реализаций случайного процесса:  , (6.6)где  — спектральная функция реализации с длительностью Т: .Эта операция возможна благодаря тому, что любая «состоявшаяся» реализация есть детерминированный сигнал. В (6.6) черта сверху означает усреднение по множеству реализаций. Заметим, что непосредственное усреднение спектральных функций приводит к нулевому результату из-за случайности и независимости фаз спектральных составляющих в различных реализациях. Функция W(), как и  , является четной, W() = W(–).В соответствии с теоремой Винера—Хинчина корреляционная функция и СПМ связаны преобразованиями Фурье:  ,  . (6.7)Принимая во внимание четность функций R() и W(), соотношения (6.7) можно представить в виде  ,  , (6.8)где F() = W()/ — «односторонняя» спектральная плотность мощности, существующая только при 0. Примерный вид СПМ и нормированных КФ для широкополосного и узкополосного случайных процессов приведен на рис. 6.3 и 6.4 соответственно, которые одновременно иллюстрируют соотношения (6.4), (6.5). Эффективной шириной функции СПМ называют значение  . (6.9)Определения  поясняет рис. 6.3, а: площадь штрихового прямоугольника должна быть равна площади под графиком функции СПМ, что следует из формулы (6.9).На практике обычно измеряют на уровне 0,5 от максимального значения СПМ, что удобнее. При этом  получается несколько меньше, чем , но близкой к ней.Ширину КФ (интервал корреляции  ) определяют как , (6.10)а измеряют по уровню 0,5 от ее максимального значения (рис. 6.3, б). КФ узкополосного процесса имеет колебательный характер, поэтому время корреляции в таком случае приближенно определяют по ее огибающей (рис. 6.4, б). В силу свойств преобразований Фурье (6.7), (6.8) время корреляции и ширина СПМ находятся в обратной зависимости:  или  , т. е. ши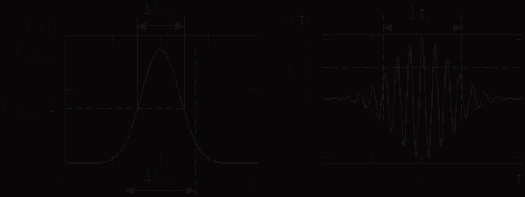рокополосному случайному процессу соответствует малый интервал корреляции и наоборот. а б Рис. 6.3  а б Рис. 6.4 Характеристики случайного процесса на выходе линейной цепи можно определить, используя спектральный или временной подход. При спектральном подходе функцию СПМ выходного процесса находят, умножая входную спектральную плотность мощности на коэффициент передачи по мощности. Этот коэффициент равен квадрату модуля комплексного коэффициента передачи цепи. Поэтому  , (6.11)где  — СПМ на выходе и входе цепи соответственно;  — комплексный коэффициент передачи. Справедливость (6.11) вытекает непосредственно из определения функции СПМ. Далее, используя соотношения (6.7) или (6.8), находят  — КФ выходного процесса.При временном подходе по известным КФ входного процесса и импульсной характеристике цепи h(t) определяют КФ процесса на выходе  (6.12)как свертку R() и  — КФ импульсной характеристики цепи h(t), причем .Справедливость выражения (6.12) следует из справедливости принципа суперпозиции для линейной цепи: выходные значения случайного процесса  можно найти методом интеграла наложения, зная входные значения  и импульсную характеристику h(t). Затем, подставив в общую формулу (6.2), получим (6.12). Далее, используя соотношения (6.7) или (6.8), находим  .В радиоэлектронике часто приходится иметь дело с прохождением случайных процессов через линейные цепи (колебательные контуры, фильтры и т. п.), полосы пропускания которых значительно меньше ширины функции СПМ входного сигнала. Для упрощения расчетов в этих случаях реальный входной шум без большой погрешности заменяют математической моделью — белым шумом. Белый шум — это случайный процесс, спектральная плотность мощности которого W() постоянна на всех частотах: W() = W0,  . Значение W0 выбирают равным значению СПМ реального входного шума в области полосы пропускания исследуемой цепи. Легко показать, что для белого шума  , где () — дельта-функция Дирака, откуда следуют соотношения: ,  , (6.13)имеющие непосредственное отношение к настоящей лабораторной работе. Наблюдение и измерение параметров случайных процессов с помощью осциллографа и анализатора спектра. Люминофор экранов осциллографа и анализатора спектра обладает определенной «памятью», послесвечением: зафиксированная за период развертки прибора осциллограмма отрезка процесса не сразу исчезает; на неё накладывается осциллограмма следующего отрезка и т. д., так что наблюдается, в сущности, сумма осциллограмм, соответствующих различным отрезкам наблюдаемого сигнала (для анализатора спектра — СПМ этих отрезков); иногда это свойство, аналогичное свойству инерционности подвижной части электромеханического прибора, используют для приближенного усреднения (интегрирования) поступающего на осциллограф сигнала. Например, в режиме автозапуска развертки и при подаче на осциллограф непрерывного случайного сигнала распределение яркости «шумовой дорожки» по Y-оси экрана будет примерно соответствовать функции плотности распределения случайного процесса (известное правило «трех сигм» для оценки дисперсии нормального случайного процесса). Аналогично объясняется наблюдение на экране спектроанализатора именно усредненной СПМ. Особый интерес представляет используемая в настоящей лабораторной работе возможность непосредственного наблюдения и оценки на экране осциллографа КФ случайного процесса. Если выбрать длительность развертки в пределах нескольких интервалов корреляции , подать на Y-вход осциллографа исследуемый сигнал, установить ждущий режим развертки осциллографа и отрегулировать уровень запуска развертки так, чтобы запуск происходил только от достаточно больших выбросов процесса (рис. 6.5, а), то изображение на экране  будет с точностью до постоянного множителя повторять КФ процесса, |
по пп. 2а, 5а;
подан АМ-сигнал 
, при этом 
, а полоса пропускания контура составляет 2; запишите выражение и постройте график выходного сигнала.
.
уровнем U значение 
становится детерминированным и дальнейшее поведение процесса определяется условной плотностью вероятности
,
. (6.14)
,
.
. (6.15)
.
. Начальный участок осциллограммы совпадает с формой КФ практически точно, так как дисперсия 
; далее, осциллограмма переходит в обычную шумовую дорожку, поскольку 
. Практически этот предел достигается при значении t, составляющем от одного до двух-трех интервалов корреляции 
процесса (t).