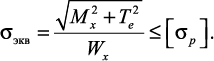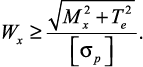|
|
СРС 5 Айбат Сарсенбаев ТПГС 20-2. Расчет элементов на внецентренное сжатие (большие эксцентриситеты)
Министерство образования и науки Республики Казахстан
Международная образовательная корпорация
Казахская головная архитектурно-строительная академия

РЕФЕРАТ
По дисциплине «Проектирование и расчет железобетонных и каменных конструкций I»
На тему: Расчет элементов на внецентренное сжатие (большие эксцентриситеты).
Выполнила: Сарсенбаев А.М.
Группа: ТПГС 20-2
Проверил: Ажгалиева Б.А.
ассоц профессор
Алматы 2022
Оглавление
Внецентренное сжатие………….………...…………………….3
Нулевая линия……………………………………………....……5 Нейтральная линия………………………………….…….........5 Ядро сечения ……………………...……………………….…….......6 Изгиб с кручением………………………………………….…….......6 Список к использованной литературы……….....……….…….......8
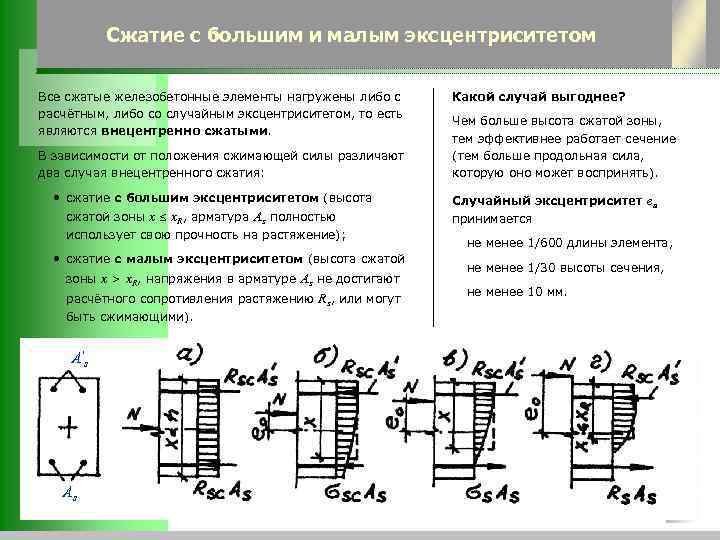
Внецентренное сжатие
Внецентренное сжатие – это вид деформации, при котором продольная сила в поперечном сечении стержня приложена не в центре тяжести. При внецентренном сжатии, помимо продольной силы (N), возникают два изгибающих момента (Mx и My).
Считают, что стержень обладает большой жесткостью на изгиб, чтобы пренебречь прогибом стержня при внецентренном сжатии.
Преобразуем формулу моментов при внецентренном сжатии, подставляя значения изгибающих моментов:
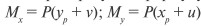
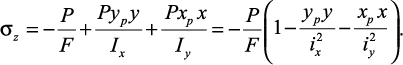
Обозначим координаты некоторой точки нейтральной (нулевой) линии при внецентренном сжатии xN, yN и подставим их в формулу нормальных напряжений при внецентренном сжатии. Учитывая, что напряжения в точках нейтральной линии равны нулю, после сокращения на P/F, получим уравнение нейтральной линии при внецентренном сжатии:
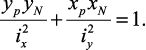
Нулевая линия при внецентренном сжатии и точка приложения нагрузки всегда расположены по разные стороны от центра тяжести сечения.
Отрезки, отсекаемые нулевой линией от осей координат, обозначенные ax и ay, легко найти из уравнения нулевой линии при внецентренном сжатии. Если сначала принять xN = 0, yN = ay, а затем принять yN = 0, xN = ax, то найдем точки пересечения нулевой линии при внецентренном сжатии с главными центральными осями:
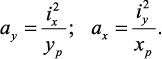
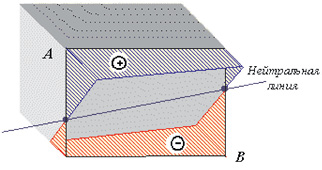
Нулевая линия
Нулевая линия при внецентренном сжатии и точка приложения нагрузки всегда расположены по разные стороны от центра тяжести сечения.

Отрезки, отсекаемые нулевой линией от осей координат, обозначенные ax и ay, легко найти из уравнения нулевой линии при внецентренном сжатии. Если сначала принять xN = 0, yN = ay, а затем принять yN = 0, xN = ax, то найдем точки пересечения нулевой линии при внецентренном сжатии с главными центральными осями:
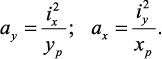
Нейтральная линия

Нейтральная линия при внецентренном сжатии разделит поперечное сечение на две части. В одной части напряжения будут сжимающими, в другой – растягивающими. Расчет на прочность, как и в случае косого изгиба, проводят по нормальным напряжениям, возникающим в опасной точке поперечного сечения (наиболее удаленной от нулевой линии).
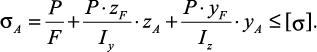
Ядро сечения 
Ядро сечения – малая область вокруг центра тяжести поперечного сечения, характерная тем, что любая сжимающая продольная сила, приложенная внутри ядра, вызывает во всех точках поперечного сечения сжимающие напряжения.
Примеры ядра сечения для прямоугольного и круглого поперечных сечений стержня.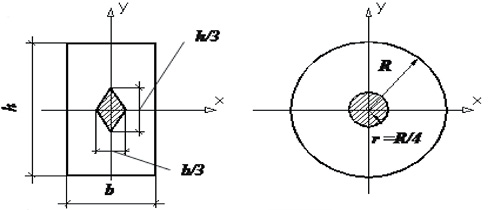
Изгиб с кручением.
Такому нагружению (одновременному действию крутящих и изгибающих моментов) часто подвержены валы машин и механизмов. Для расчета бруса необходимо прежде всего установить опасные сечения. Для этого строятся эпюры изгибающих и крутящих моментов.
Используя принцип независимости действия сил, определим напряжения, возникающие в брусе отдельно для кручения, и для изгиба.
При кручении в поперечных сечениях бруса возникают касательные напряжения, достигающие наибольшего значения в точках контура сечения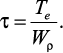 При изгибе в поперечных сечениях бруса возникают нормальные напряжения, достигающие наибольшего значения в крайних волокнах бруса При изгибе в поперечных сечениях бруса возникают нормальные напряжения, достигающие наибольшего значения в крайних волокнах бруса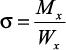 . .
Касательные напряжения значительно меньше напряжений от крутящего момента, поэтому ими пренебрегают. Опасное сечение бруса будет у заделки, где действуют максимальные напряжения от изгиба и кручения.
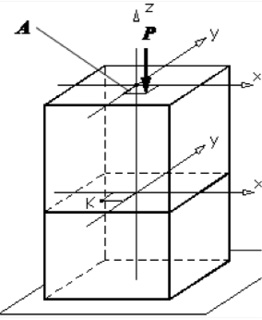
Исследуем напряженное состояние в наиболее опасной точке A (рис. 46). Так как напряженное состояние двухосное, то для проверки прочности применяем одну из гипотез.
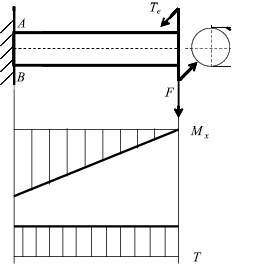
Рис. 46. Эпюры изгибающих и крутящих моментов
Применяя третью теорию прочности
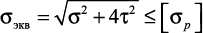
и учитывая, что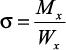 и и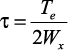 , получаем: , получаем:
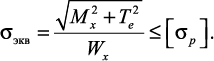
Для подбора сечения находим требуемый момент сопротивления
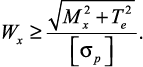
Список использованной литературы 
https://monographies.ru/ru/book/section?id=7041
http://normativa.ru/snips/section-2-design-standards/snip-2-05-03-84-mosty?start=31
https://present5.com/presentation/59349885_347176663/image-138.jpg |
|
|
 Скачать 417.11 Kb.
Скачать 417.11 Kb.


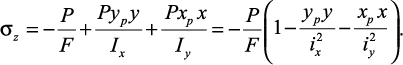
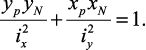

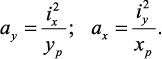

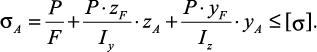


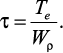 При изгибе в поперечных
При изгибе в поперечных 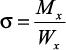 .
.
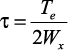 , получаем:
, получаем: