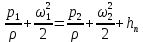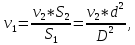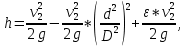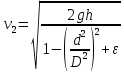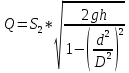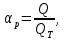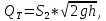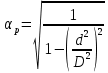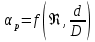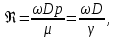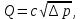Курсовая 30-62 ТИП. Расчет сужающего устройства
 Скачать 2.76 Mb. Скачать 2.76 Mb.
|
2.4 Уравнение БернуллиУравнение Даниила Бернулли, полученное в 1738г., является фундаментальным уравнением гидродинамики. Оно дает связь между давлением P, средней скоростью υ и пьезометрической высотой z в различных сечениях потока и выражает закон сохранения энергии движущейся жидкости. С помощью этого уравнения решается большой круг задач. При применении уравнения Бернулли для решения практических задач гидравлики следует помнить два основных условия: 1) уравнение Бернулли может быть применено только для тех живых сечений потока, в которых соблюдаются условия плавно изменяющегося движения. 2) гидродинамическое давление р и, следовательно, высоту положения z можно относить к любой точке живого сечения так как для любой точки живого сечения потока при плавно изменяющемся движении есть величина постоянная, что обычно приемлемо для горизонтальных участков трубопроводов. Разберем применение уравнения Бернулли на примере измерения скорости и расхода жидкости в трубопроводе. В практической деятельности используются различные способы измерения расхода жидкостей, однако, наибольшее распространение в настоящее время получили нормальные дроссельные расходомеры. Под термином «нормальные» следует понимать объединенные государственными нормалями геометрически подобные, как бы стандартные устройства. К нормальным дроссельных расходомерам относятся диафрагмы, сопла и трубы Вентури. Идея измерения расхода жидкости дроссельными расходомерами заключается в следующем. В потоке жидкости устанавливается сужающее поток устройство. При движении жидкости по такому каналу поток последовательно перемещается от широкого сечения к узкому. В соответствии с уравнением Бернулли в узком сечении потока, по сравнению с широким сечением доля кинетической составляющей энергии должна быть больше, а составляющей энергии меньше. Между разностью потенциальных энергий в широком и узком сечениях и величиной кинетической энергии в узком сечении (точнее приращением кинетической энергии) существует однозначная связь, обусловленная законом сохранения энергии (уравнение Бернулли). Запишем уравнение Бернулли для выбранных сечений, приняв за плоскость сравнения 0-0 (сечение, проходящее через ось трубы). Тогда уравнение Бернулли запишется так:
где 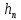 – потери напора между сечениями; р1 и р2 – давления соответственно в сечениях А и В; v1 и v2 – скорости потока соответственно в сечениях А и В; – потери напора между сечениями; р1 и р2 – давления соответственно в сечениях А и В; v1 и v2 – скорости потока соответственно в сечениях А и В; 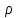 - плотность протекающего вещества; - плотность протекающего вещества; 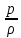 - статический напор или потенциальная энергия потока; - статический напор или потенциальная энергия потока; 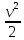 – скоростной напор, или кинетическая энергия потока. – скоростной напор, или кинетическая энергия потока.Используя уравнение расхода 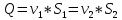 , получим: , получим:
где S2 - площадь широкого сечения, м2; S1 – площадь узкого сечения, м2. Совместное решение уравнений приводит к выражению:
откуда скорость жидкости в сечении 2-2:
Тогда объемный расход жидкости равен:
Отношение действительного расхода жидкости к теоретическому расходу называют коэффициентом расхода дроссельного расходомера:
а с учетом того, что:
для идеальной жидкости получаем:
Величина 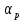 для реальной жидкости зависит также от критерия Рейнольдса, то есть: для реальной жидкости зависит также от критерия Рейнольдса, то есть:
Поскольку при прохождении вещества через сужающее устройство плотность вещества уменьшается и давление падает, в формулах (24) и (25) принимается плотность среды перед сужающим устройством. Полученные уравнения справедливы для тех случаев, когда скорость потока не достигает критической величины, т. е. скорости звука. Коэффициент расхода, определяемый опытным путем, зависит от числа подобия критерия Рейнольдса (Re) - величины, связывающей геометрические параметры потока, силы инерции (кинетической) и силы вязкости (работы сил внутреннего трения жидкости):
где ω - средняя скорость среды в трубопроводе; D - внутренний диаметр трубопровода; μ - коэффициент динамической вязкости; γ = 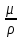 – коэффициент кинематической вязкости. – коэффициент кинематической вязкости.Параметр подобия Re является величиной безразмерной. При больших числах подобия коэффициенты расхода дроссельных органов становятся постоянными, т. е. не зависящими от скорости, вязкости и плотности протекающего вещества. Число подобия, при котором прекращается эта зависимость, называется предельным числом подобия Reпр. Оно зависит от формы сужающего устройства и величины m. Геометрически подобные сужающие устройства имеют одно и то же значение Reпр. Таким образом, коэффициент расхода для данного сужающего устройства является постоянной величиной только при условии Re 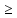 Reпp. Поэтому для определения исходного коэффициента расхода необходимо знать величину Re. Расходомер переменного перепада давления основан на изменении перепадов давления, которые возникают, когда поток жидкости, газа или пара проходит через шайбу или сопло. Преимущество данного расходомера заключается в отсутствии движущихся частей. Reпp. Поэтому для определения исходного коэффициента расхода необходимо знать величину Re. Расходомер переменного перепада давления основан на изменении перепадов давления, которые возникают, когда поток жидкости, газа или пара проходит через шайбу или сопло. Преимущество данного расходомера заключается в отсутствии движущихся частей.В случае измерения расхода жидкости при постоянной температуре, вычислив постоянные величины и приведя к единице измерения расхода, получаем:
где коэффициент с включает все величины, постоянные для данной установки и не изменяющиеся в процессе измерения. Одним из основных устройств является дифференциальный манометр, который будет выбран в конце расчета. Для определения сужающего устройства используем расчетную часть. |