Детали машин шпоры. Расчеты на прочность. Виды циклов. Контактное напряжение
 Скачать 1.33 Mb.
|
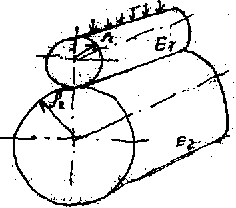 Расчет производится по формуле Герца-Беляева. Зависимость Герца-Беляева для нормальных напряжений в месте контакта двух сухих неподвижных цилиндров из изотропных материалов 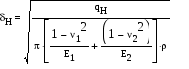 qH – удельная погонная сила по нормали к профилю; 1, 2 – коэффициент пуансона; E1, E2 – модуль упругости материала, – радиусы кривизны каждого цилиндра. 1/=1/1 1/2, «+» для внешного зацепления, «–» для внутренного зацепления. Формула Герца-Беляева для пары зубчатых колес   ZE – коэффициент, учитывающий свойства материалов   Z – коэффициент, учитывающий суммарную длину контактных линий  – для прямозуб. – для косозубыхРасчет передач на сопротивление усталости при изгибе Расчет выполняется при предположениях, что зуб нагружен силой FH, в зацеплении находится одна пара зубьев, а также силы трения отсутствуют. 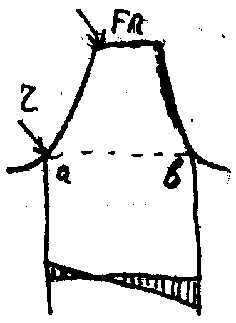 Наибольшее трение в точке b, однако растягивающий эффект в точке a, r – радиус выпуклости зуба,  []FYFS – коэффициент, учитывающий форму зуба и концентрацию напряжения Y – коэффициент, учитывающий угол наклона Y – коэффициент, учитывающий перекрытие зубьев. Y= 1/£ – для косозубой передачи, Y = 1 для прямозубой передачи. m выбрать по возможности меньше, z соответственно больше. m=(0,01 ... 0,02)aW. В случае открытой передачи 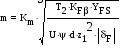 Расчет по модулю Если прочность на изгиб является основным критерием работоспособности. Расчет ведется в форме определения модуля по заданным числам зубьев с последующей проверкой контактной прочности (или формула выше) 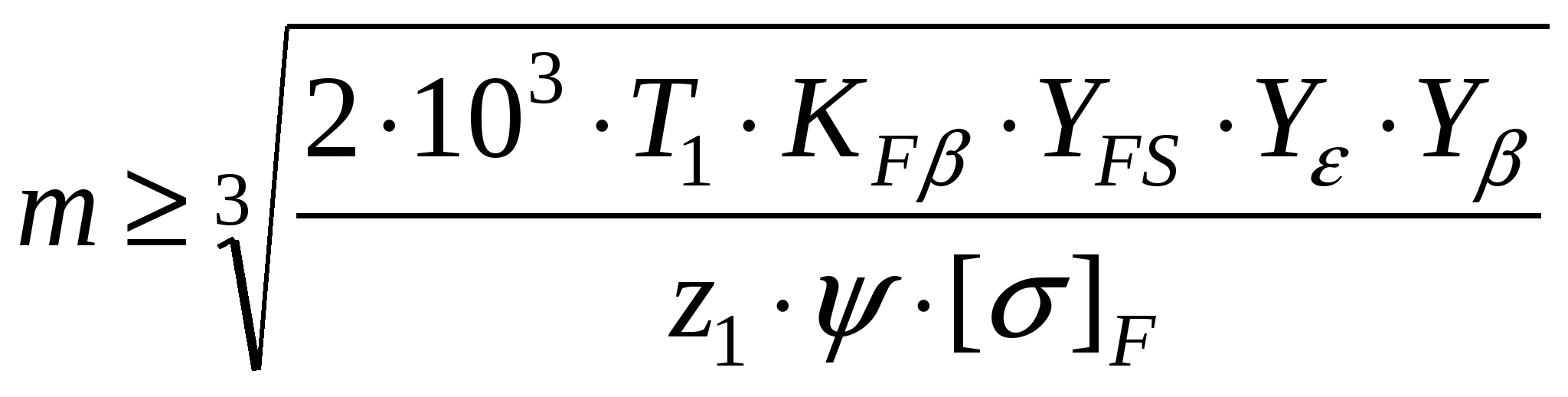 Допускаемые напряжения Для расчета переменный режим заменяем эквивалентным. 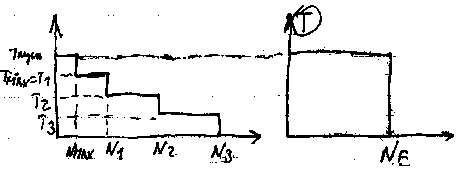 NE = N H , NFE=N F, N – суммарное число циклов = 60nnЗLh, где Lh – ресурс работы передачи, nЗ– число зубьев зацеплении, n– частота вращения.  p = qH/2, p = qF. Допускаемые контактные и изгибные напряжения устанавливаются на основе кривых усталости 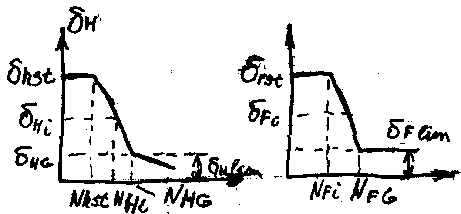 NHG = 30HB2,4, NFG = 4106. Если NHENHG, то qH=6,если NHE>NHG, то qH=20. Коэффициенты долговечности:  и  qF = 6 для нормальных умеренных колес, qF = 9 для поверхностно-закаленных колес. Методы повышения контактной и изгибной прочности Для повышения контактной прочности используется: 1. увеличение твердости рабочей поверхности зубьев путем: а) изменением материала б) изменением режима термообработки в) применением поверхностных обращений 2. исправление геометрического зацепления путем: а) увеличения смещения инструмента б) применением нестандартного зацепления в) увеличением угла наклона зуба 3. уменьшение расчетной нагрузки путем уменьшения коэффициента KH Для повышения изгибной прочности применяют: 1. увеличение модуля с одновременным уменьшением числа зубьев (без подрезания) 2. применить смещение инструмента, т.е. увеличить угол зацепления £. 3. применить смещение Х для шестерни за счет колеса 4. уменьшить коэффициент KF 5. поверхностное упрочнение у корня зуба (наклеп, цементация и т.д.) 6. увеличение радиуса кривизны переходной кривой у основания зуба. Определение основных размеров зубчатой передачи Начальный диаметр шестерни:  Расчетная ширина колеса:  Межосевое расстояние:  Принимаем стандартное межосевое расстояние Пересчитываем ширину колеса:  Принимаем стандартную ширину колеса. Находим ширину шестерни: bW1 = bW2 + 5 Определение геометрии зацепления зубчатой передачи Модуль: m=(0,01...0,02)aW Число зубьев шестерни:  Число зубьев колеса: Z2 = Z1U Угол наклона зуба:  Осевой шаг:  Коэффициент осевого перекрытия: = bW2/PX Начальный диаметр: dW=mz / cosW. Диаметр выступов: d a = dW + 2m Диаметр впадин: d f = dW – 2,5m Коэффициент торцевого перекрытия: 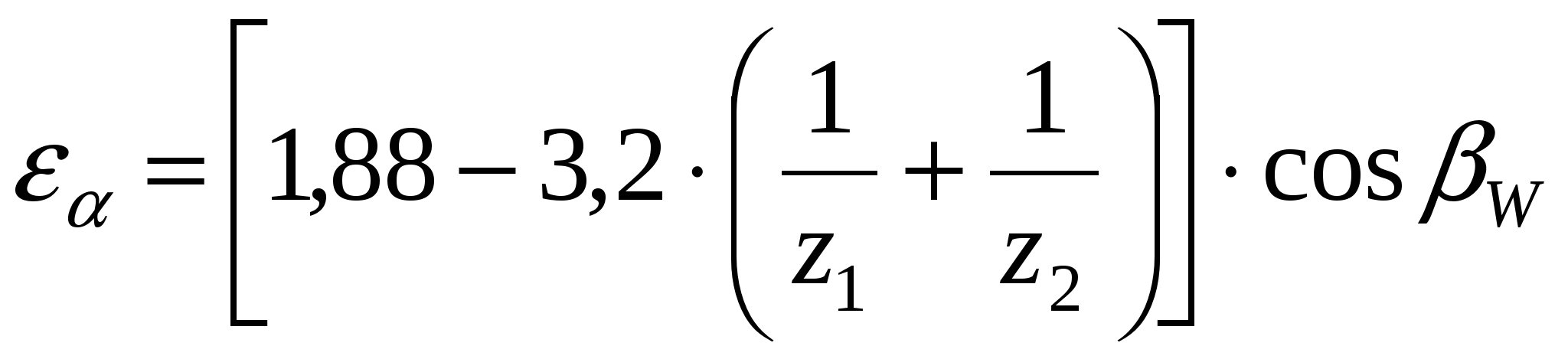 ЧЕРВЯЧНЫЕ ПЕРЕДАЧИ
Червяк – винт с трапециидальной или близкой по форме резьбой Достоинства: – Возможность получения больших передаточных отношений – Большая плавность работы – Малая шумность – Компактность Недостатки: – Большое трение в передачах большой нагрев из-за, большого скольжения, что требует применения дорогостоящей оловянной бронзы – Очень низкий КПД (60-95%) – Износ зубьев – Мощность не выше 50 кВт Геометрия червячной передачи Червяк является ведущим, колеса ведомым. Червячная передача бывает следующих типов: 1. Цилиндрическая – делительная и начальная поверхности червяка и колеса круговые цилиндры. 2. Глобоидные – делительная поверхность является частью вогнутой поверхности тора (глобоида)
Виды цилиндрических червяков Бывают линейчатые и нелинейчатые. Линейчатые образуются винтовым движением прямой линии, а нелинейчатые винтовым движением конической или тороидальной формы. К линейчатым относится 3 типа: 1. Архимедов ZA 2. Эвольвентный ZJ 3. Конвалютный ZN Нелинейные обозначаются как ZT Геометрические параметры червяка и колеса m – осевой модуль червяка p = m – расчетный осевой шаг червяка pX = p z1 – ход витка (шаг винтовой линии) = arctg (pX / d1) – делительный угол подъема линии витка Делительный диаметр червяка: d1 = mz1 / tg , причем z1 / tg = q – коэффициент диаметра червяка. d2 = mz2 – число зубьев колеса a = (d1 + d2) / 2 – межосевое расстояние Кинематика червячных передач U = 1/2 = n1/n2 = z2/z1 За 1 оборот червяк повернется на угол , а колесо на угол 2 = pX / d2. 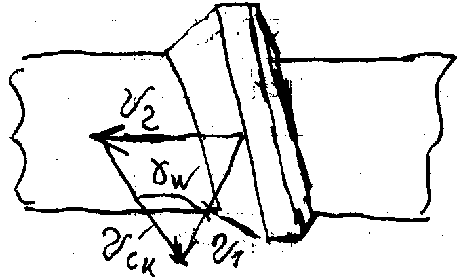 V1 – окружная скорость червяка на диаметре dW1, V2 – окружная скорость колеса на диаметре dW2, W – начальный угол подъема витка Силы червячном в зацеплении 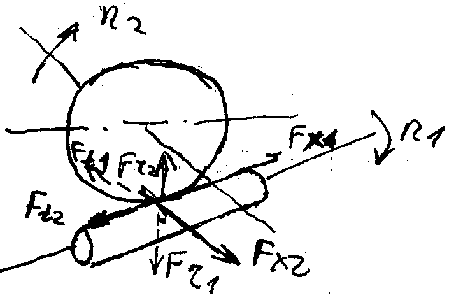 Окружная сила червяка (касательная к начальной окружности) Ft1 = 2000T1/dW1 Осевая червяка (вдоль оси) FX1= Ft2 Радиальная червяка (к центру окружности) FR1=FR2=Ft2tg £, Окружная колеса Ft2 = 2000T2/dW2 Осевая колеса FX2=Ft1. Приведенный коэффициент передачи и КПДчервячного редуктора КПД в червячном редукторе определяют по зависимости  Приведенный угол трения = arctg f, f = f / cos £, где f – приведенный коэффициент трения, f – коэффициент трения. Чем мягче материал колеса, тем более скорость скольжения, тем чище рабочая поверхность и меньше приведенный угол трения. При > W передача самотормозящая W = arctg (z1/(q+2X), где W – начальный угол подъема витка, q – коэффициент диаметра червяка, x – коэффициент смещения. Общий КПД передачи определяется как = зацепления разбрызг. масла Критерий рабососпособности Работоспособность червячной передачи ограничивается: 1) стойкостью рабочих поверхностей зубьев; 2) изгибной прочностью зубьев; 3) предельной допустимой температурой масла или корпуса; 4) прочностью и жесткостью червяка. Основные виды разрушений 1) усталостное выкрашивание 2) заедания 3) механическое изнашивание материалов червяка и венцов колес. Большое скольжение в зацеплении требует, чтобы материал червяка и венца являлся антифрикционной парой. Червяк изготавливают из углеродистых легированных сталей, реже из чугунов, а венец колеса из бронзы, латуни, чугуна и неметаллических материалов. Коэффициент нагрузки K = K + KV, где K – коэффициент равномерности распределения нагрузки вдоль линии контакта вследствие деформации червяка, KV – коэффициент, учитывающий динамическую нагрузку, возникающую в зацеплении. В формуле определения K (см. приложение) – коэффициент деформации червяка, ср – средняя относительная нагрузка. KV зависит от скорости скольжения, точности изготовления передачи. (Формула в приложении) nT – степень точности. Формула Герца-Беляева для червячной передачи  E1, E2 –модуль упругости, 1, v2 – коэффициент Пуассона, Wn – погонная нагрузка, – приведенный радиус кривизны. Формула Герца для червячного зацепления:  []H МПа, где ZM – коэффициент, учитывающий механические свойства материалов червячной пары, ZH – коэффициент, учитывающий форму рабочих поверхностей червячной пары, Z – коэффициент, учитывающий суммарную длину контактных линий, Z – коэффициент, учитывающий условный угол охвата, d2 – делительный диаметр колеса, dW1 – начальный диаметр червяка, K– коэффициент нагрузки. ZH = [cos2 W / sin2 £nW] при Архимедовом червяке (ZK), ZH = [cos2 W / (cos £n sin b cos )] при эвольвентном червяке (ZJ), где £nW – угол профиля в нормальном сечении на начальном цилиндре червяка, £n – угол профиля в нормальном сечении зуба рейки, сопряженной с червяком, b – основной угол подъема витка червяка, – делительный угол подъема. Z = [1 / (£ K)], где £ – коэффициент осевого перекрытия. Расчет рабочих поверхностей зубьев колес по контактным напряжениям Расчет []H базируется на кривых усталости. 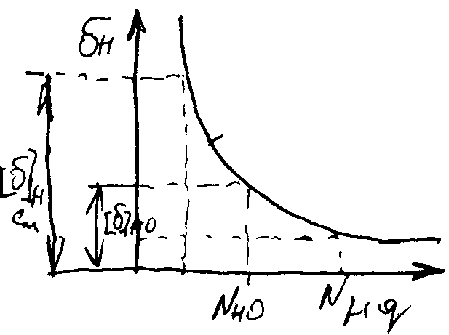 Hm N = const, где m – степень кривой усталости, m = 8 при контакте. []HO – допускаемое контактное напряжение при базовом числе циклов NHO=107. В передачах с венцами из оловянных бронз допускаемые напряжения контакта [H] определяется из отсутствия усталостного выкрашивания рабочей поверхности за рабочий срок службы LH: []H = []HO CV KHL 4T2 / KП, где CV – коэффициент, учитывающий влияние скорости скольжения на интенсивность изнашивания зубьев, KHL – коэффициент долговечности  NHE – эквивалентное число циклов нагружений, KП = Tпуск/Tmax– коэффициент перегрузки. В передачах с колесам и из безоловянной бронз, латуни и чугунов []H определяют из отсутствия заедания: []H = []HO CV, где CV – коэффициент, учитывающий влияние скорости скольжения на проявление заедания. Проверка зубьев на статическую контактную прочность H ПИК = HKП []H СТАТ , где KП – коэффициент перегрузки. Меры повышения контактной прочности 1. Увеличение твердости и чистоты обработки рабочей поверхности червяка; 2. Применение червяка с вогнутым профилем витков; 3. Выбор более современного способа отливки венца для оловянного способа; 4. Уменьшение коэффициента диаметра червяка q для венцов из безоловянной бронз, латуни, чугунов. Чем скорость скольжения выше, тем меньше опасность заедания. 5. Выбор смазочного материала, способного образовывать на поверхности контакта более прочные пленки. Расчет зубьев червячного колеса на изгиб  []F МПа, где Y – коэффициент, учитывающий суммарную длину контактных линий, Y – коэффициент, учитывающий угол охвата, Y – коэффициент, учитывающий форму зуба (зависит от приведенного числа зубьев ZV), K – коэффициент нагрузки. В передачах с большим передаточным числом (больше 70), а также открытые передачи при проектировании рассчитываются по изгибной прочности зубьев (по модулю): |
