Горизонтальный одноступенчатый редуктор. Вариант 8 - схема 3. Расшифровка подписи Члены комиссии подпись расшифровка подписи
 Скачать 0.65 Mb. Скачать 0.65 Mb.
|
3.2 Расчет тихоходного вала3.2.1 Предварительный расчет тихоходного вала Расчет выполняется на кручение по пониженным допускаемым напряжениям [𝜏𝑘] МПа. Ориентировочно определим диаметр вала в наименьшем сечении: 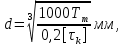 где 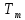 Нм – крутящий момент в опасном сечении вала,[𝜏𝑘]МПа – пониженные допускаемые напряжения на кручение, σb МПа – предел прочности материала вала. Нм – крутящий момент в опасном сечении вала,[𝜏𝑘]МПа – пониженные допускаемые напряжения на кручение, σb МПа – предел прочности материала вала.Твердость заготовки 179…207 HB; σb=600МПа. Тогда допускаемое напряжение на кручение [𝜏𝑘]= 0,025  σb = 0,025 σb = 0,025  600 = 15 МПа. 600 = 15 МПа.Тогда диаметр хвостовика вала 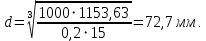 Принимаем диаметр d = 75 мм из нормального ряда линейных размеров. Консольная нагрузка: 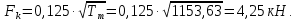 3.2.2 Определение опорных реакций Горизонтальная плоскость Σm(F)B= 0 Fa· 0,5d1 – Fr· L3 + RDг· L0 = 0 RDг = 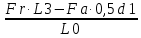 = = 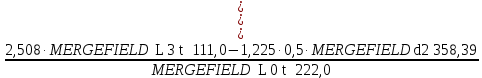 = 0,265 кН. = 0,265 кН.Σm(F)D= 0 Fr · L3 +Fa ·0,5d1 – RBг· L0 = 0 RBг = 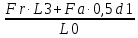 = = 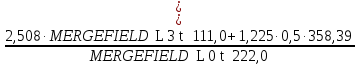 =2,243 кН. =2,243 кН.Проверка: ΣFу= 0 RВг– Fr + RDг = 0 2,243– 2,508 +0,265 = 0 Вертикальная плоскость Σm(F)D= 0 Ft· L3 – RBв· L0 +Fk· (Lk+ L0) = 0 RBв = 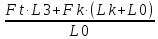 = = 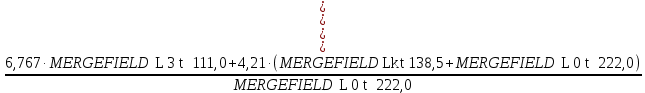 = 10,22 кН. = 10,22 кН.Σm(F)B =0 Fk· Lk –Ft· L3 + RDв· L0 = 0 RDв = 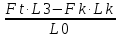 = = 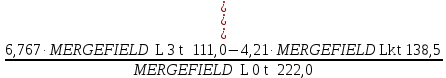 =0,76 кН. =0,76 кН.Проверка: ΣFу= 0 –Fk + RВв–Ft + RDв = 0 –4,21+ 10,22–6,767 +0,76= 0 3.2.3 Построение эпюр изгибающих и крутящих моментов для тихоходного вала Изгибающие моменты в сечении С (горизонтальная плоскость) МхСВ = L3· RBг = 111,0 · 2,243= 249 Нм; МхСD = МхСВ – 0,5d2 Fa = 249– 0,5·358,39· 1,225= 29,5 Нм. Изгибающие момент в сечении B (вертикальная плоскость) МуВ = –Lk·Fk = –138,5· 4,21=-583 Нм. Изгибающие момент в сечении С (вертикальная плоскость) МуС = –(Lk + L3)·Fk +L3·RBв = –(138,5 + 111)·4,21+111·10,22= 84 Нм. Суммарный изгибающий момент 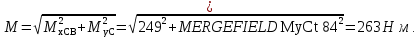 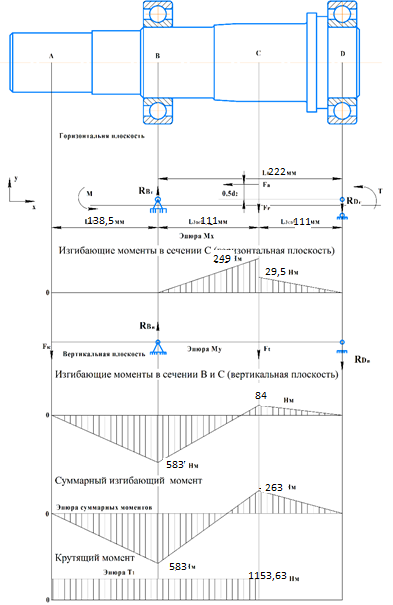 Рисунок 3 – Эпюры изгибающих и крутящих моментов на тихоходном валу 3.3 Расчет тихоходного вала в сечении В1) Определение нагрузок В сечении действуют: Изгибающий момент M= 583 Нм; Крутящий момент Тт = 1153,63 Нм; Осевая сила Fa= 1,225 кН. 2) Геометрические характеристики опасного сечения Значения площади поперечного сечения A, осевого 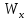 и полярного и полярного 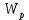 моментов сопротивлений для типовых поперечных сечений определяют по формулам. моментов сопротивлений для типовых поперечных сечений определяют по формулам.Осевой момент сопротивления: 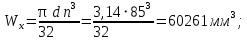 Полярный момент сопротивления: 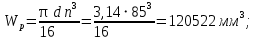 Площадь сечения: 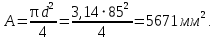 3) Определение напряжений Напряжения изгиба меняются по симметричному циклу с амплитудой: 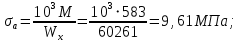 Средние нормальные напряжения: 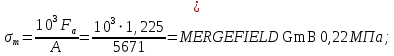 Касательные напряжения меняются по отнулевому циклу: 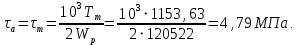 4) Пределы выносливости Пределы выносливости материала при симметричном цикле изгиба и кручения определяются по следующим формулам: для углеродистых сталей: 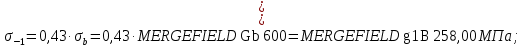 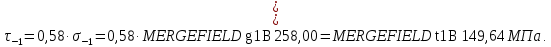 здесь 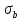 – предел прочности материала вала – предел прочности материала вала5) Эффективные коэффициенты концентрации напряжений и коэффициенты влияния размера поперечного сечения. Для посадки с натягом 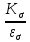 определяется из Табл. 7,5 определяется из Табл. 7,5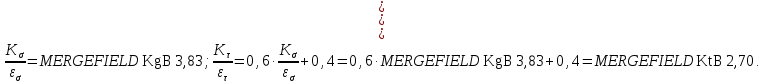 6) Коэффициент влияния шероховатости поверхности. Поверхность вала под подшипник получена чистовым шлифованием с 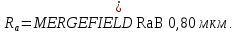 KF – коэффициент влияния шероховатости поверхности, определяется в зависимости от 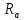 KF= KF=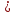 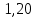 . .7)Коэффициентчувствительности к асимметрии цикла. 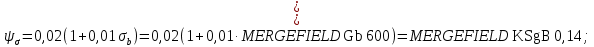 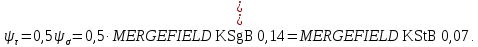 8) Коэффициент влияния упрочнения. Примем, что на участке вала с опасным сечением упрочнение отсутствует. KV - коэффициент влияния упрочнения, KV=1. 9) Коэффициенты перехода от пределов выносливости образца к пределам выносливости детали. 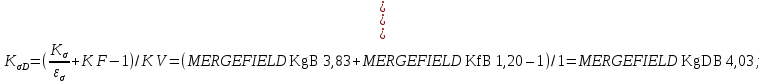 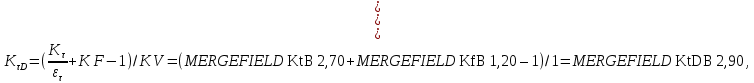 где 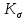 и и 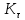 - эффективные коэффициенты концентрации напряжений - эффективные коэффициенты концентрации напряжений 10) Коэффициенты запаса прочности Значения 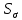 и и 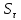 определяют по формулам определяют по формулам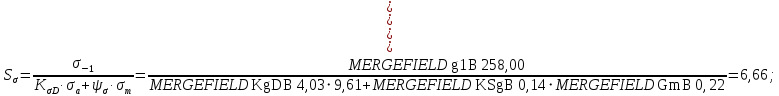 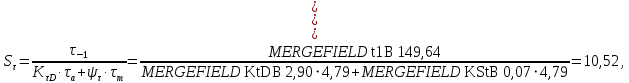 где 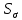 и и 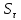 – коэффициенты запаса прочности по нормальным и касательным напряжениям. – коэффициенты запаса прочности по нормальным и касательным напряжениям.Суммарный коэффициент запаса прочности 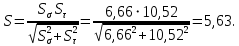 Условие прочности вала имеет вид 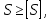 где [S] – допускаемый коэффициент запаса прочности. Рекомендуемое значение 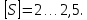 Усталостная прочность вала в сечении В обеспечена. |
