«Разработка программного комплекса моделирования оценок характер. Разработка программного комплекса моделирования оценок характеристик и точности навигационных параметров технических средств судовождения

• Название: Разработка программного комплекса моделирования оценок характеристик и точности навигационных параметров технических средств судовождения
• Дата: 27.05.2022
• Размер: 1.47 Mb.
• Имя файла: «Разработка программного комплекса моделирования оценок характер.doc
• Тип: Документы; #552928
• страница: 3 из 12

1.1.3 Теоретическая оценка

Для теоретической оценки параметров чувствительного элемента необходимо воспользоваться уравнением, характеризующим закон движения его главной оси в азимуте в режиме затухающих колебаний:
, (1.2)

параметры В, С, Н и выбираются для расчетов из этой же работы.

Так как характеристическое уравнение, соответствующее данному дифференциальному уравнению, является алгебраическим уравнением третьей степени, но необходимо, пользуясь формулой Кардана, или на ЭВМ рассчитать корня этого уравнения для заданной широты, т.е.

(1.3)

Приняв угол начального отклонения главной оси чувствительного элемента равным экспериментальному отклонению, и с учетом найденных значений найдем с помощью ЭВМ закон движения чувствительного элемента, используя следующую аналитическую зависимость:
(1.4)
где t изменяемся от 0 до 21600 с, с шагом 180 с (12 точек). Полученную траектория движения оси чувствительного элемента представить в виде графика и снять с него значения периода затухающих колебаний и фактора (средние значения). Затем сравнить эти значения со значениями, найденными по формулам , и со значениями, полученными при экспериментальном определении Т_ли f. Результаты представляются в виде таблице 1.

Таблица 1.1 Сравнительная оценка параметров

Параметры	Метод разработки		Расчет по формулам
	Экспериментальная кривая	Теоретическая кривая
f

1.2 ГИРОКОМПАС НА ПОДВИЖНОМ ОСНОВАНИИ

1.2.1 Влияние постоянного режима движения судна на параметры гирокомпаса

При движении судна по шарообразной поверхности Земли возникает дополнительное вращение плоскости горизонта, которое складывается с угловыми скоростями вращения Земли. Рассмотрим это явление для судна, идущего постоянными курсом и скоростью.

Как известно, вектор 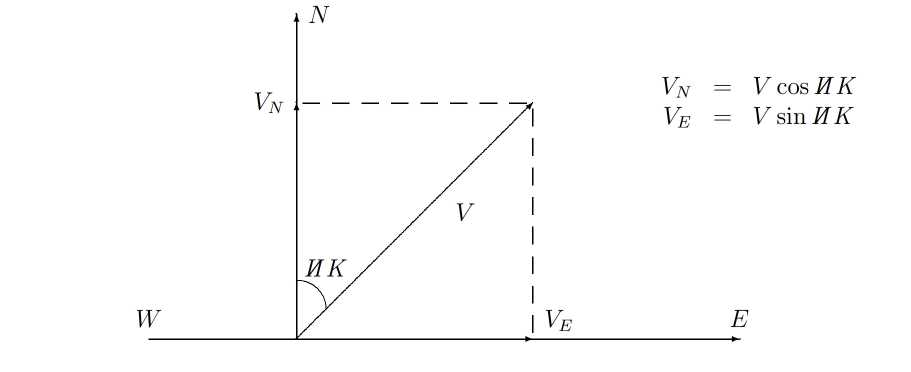скорости судна может быть разложен на северную и восточную составляющие (Рисунок 1.1).


Рисунок 1.1 – Вектор скорости
Так как радиус параллели , то угловая скорость движения судна по параллели будет

(1.5)

Очевидно, что вектор 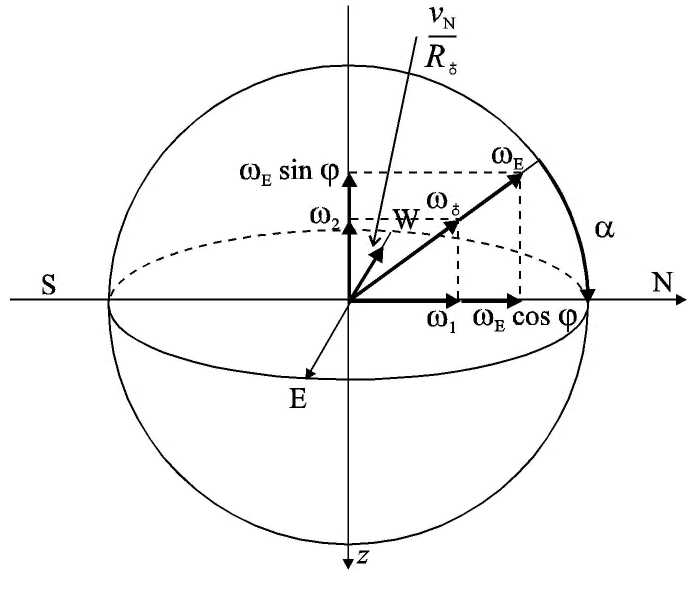направлен по земной оси, так как вокруг нее происходит вращение судна при его движении по параллели. Следовательно, произойдет сложение векторов . На Рисунке 2 показано, что эти векторы раскладываются на вертикальные и горизонтальные составляющие.



Рисунок 2.1- Составляющие горизонтального и вертикального вектора скорости
Таким образом, к вертикальной составляющей угловой скорости вра­щения Земли добавится:

(1.6)

а к горизонтальной составляющей добавится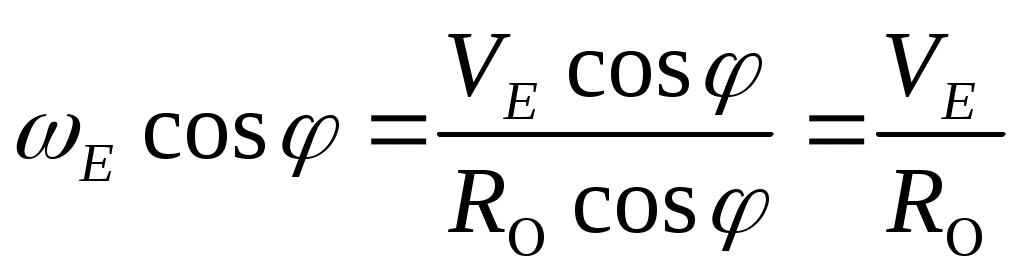

(1.7)

При движении судна по меридиану со скоростью возникает его дополнительное вращение вокруг параллели с угловой скоростью

(1.8)

При малом угле 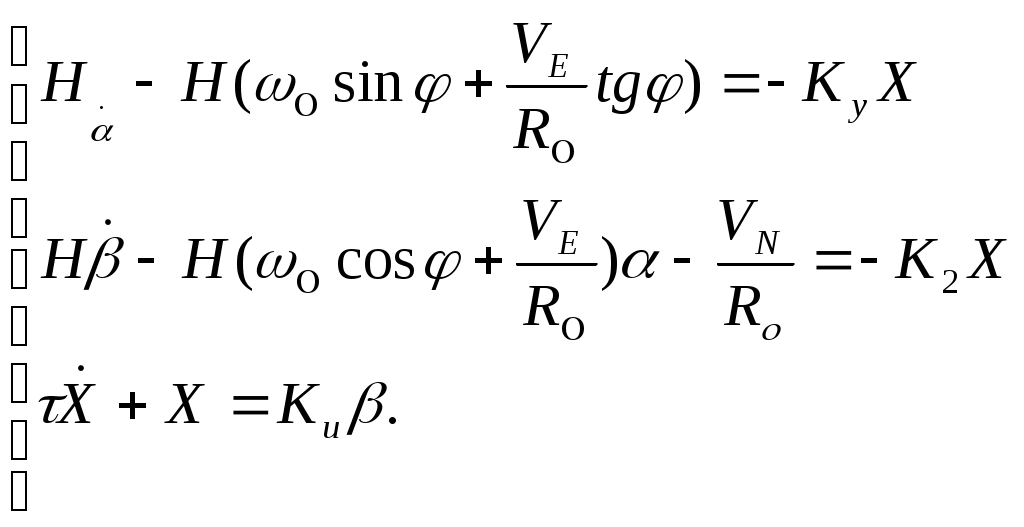проекция на ось у по величине практически равна длине самого вектора. Таким образом, в системе уравнений (1.9) к первому уравнению прибавится составляющая (1.6), а ко второму составляющие (1.7) и (1.8)

(1.9)

Получены уравнения движения ЧЭ гирокомпаса для случая, когда к нему не приложены корректирующие моменты. В уравнениях отобра­жено вращение горизонта в инерциальном пространстве, как вследствие вращения Земли, так и вследствие движения судна. Последнее обстоятельство вносит в показания гирокомпаса дополнительные погрешности. Данные погрешности, а также широтная девиация исключаются из его показаний с помощью корректирующих моментов. Также при движении судна с постоянными скоростью и курсом изменяется такие параметры компаса, как направляющий момент ( ), период собственных незатухающих ( ) и затухающих ( ) колебаний, время прихода в меридиан и точность показаний.

Так, для гирокомпаса типа “КУРС” расчетные формулы могут быть записаны в виде (2.0, 2.1, 2.2, 2.3, 2.4):

(2.0)
(2.1)
(2.2)
(2.3)
(2.4)