лекция. Лекция 13. Развертки поверхностей
 Скачать 1.4 Mb. Скачать 1.4 Mb.
|
|
13.1. Построение разверток поверхностей многогранников Напомним, что многогранником называют пространственную геометрическую фи-гуру, со всех сторон ограниченную плоскими многоугольниками (гранями). Развертка многогранника представляет собой плоскую фигуру, которая получается при совмеще-нии граней многогранника с плоскостью. Процесс построения развертки поверхности многогранника сводится к построению истинных величин его граней, что непосредст-венно связано с определением натуральной (истинной) длины каждого ребра много-гранника. Рассмотрим построение разверток наиболее распространенных многогран-ных поверхностей – поверхностей пирамид и призм. 13.1.1. Развертка пирамиды Поверхность n-угольной пирамиды включает в себя основание (плоский n-угольник) и боковую поверхность, состоящую из nтреугольников. Для построения раз-вертки пирамиды необходимо определить натуральные величины боковых ребер и сто-рон основания. На рис. 13.1, аизображена треугольная пирамида ABCS. Основанием пирамиды является треугольник АВС, расположенный в плоскости, параллельной гори-зонтальной плоскости проекций, поэтому стороны основания AB, BC, AC проецируются на П1в натуральную величину. Длины боковых ребер пирамиды определяются с помощью вспомогательных пря-моугольных треугольников. Вспомогательные треугольники имеют общий катет S2O0(разность высот концов боковых ребер пирамиды). Другой катет равен длине горизон-тальной проекции соответствующего ребра. Например, в треугольнике S2O0A0катет S2O0равен разности высот точек Sи А. Другой катет O0А0равен горизонтальной проек-ции ребра SA: O0A0=S1A1. Истинная длина ребра SAравна величине гипотенузы S2A0. Аналогично длина ребра SB равна S2B0, а длина ребра SC равна S2C0. 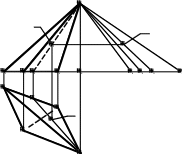 S2 S2 K2 K0 A A 1 K2 K0 A A 1A2 B B2 12 C2 O0 A1 11 C1K1 C0B010 A0 K A C B1 S1 а) Рис. 13.1 SK=S2K0 б) S Развертка боковой поверхности пирамиды состоит из трех примыкающих друг к другу треугольников (рис. 13.1, б), конгруэнтных соответствующим граням пирамиды. Например, треугольник ACS(развертка соответствующей грани пирамиды) построен по известной длине стороны ACи найденным на рис. 13.1, адлинам боковых ребер пира-миды AS и CS. К развертке боковых граней пирамиды пристраиваем ее основание ABC. Пусть на поверхности пирамиды отмечена точка K. Чтобы найти положение этой точки на развертке, проводим через Kвспомогательную прямую S-K-1, отмечаем на развертке точку 1и с помощью прямоугольного треугольника S2O010находим истин-ную длину отрезка SK=S2K0. Откладывая этот отрезок на развертке от точки Sвдоль прямой S-1, находим точку K. 13.1.2. Развертка призмы На рис. 13.2, аизображена наклонная призма. Призма расположена таким образом, что ее основание параллельно горизонтальной плоскости проекций, поэтому на П1ос-нование ABCпризмы проецируется в натуральную величину A1B1C1. Боковые ребра призмы параллельны фронтальной плоскости проекций, поэтому на П2они проециру-ются без искажения. Развертка боковой поверхности призмы может быть получена способомнормально-госечения.Для этого боковую поверхность призмы рассекают фронтально- проецирующей плоскостью Σ, перпендикулярной боковым ребрам призмы. Истинную форму нормального сечения 142434определяют способом замены плоскостей проекций. Чтобы построить развертку призмы, нормальное сечение 142434“разворачиваем” в прямую линию нормального сечения 1231и через каждую точку проводим перпенди-куляры к этой прямой (рис. 13.2, б). На каждом из построенных перпендикуляров от-кладываем по обе стороны от линии нормального сечения отрезки боковых ребер, из-меренные на плоскости П2до нормального сечения и после него. Например, отрезки A-1и 1-A′на развертке равны отрезкам A212и 12A′2на фронтальной проекции призмы. Точно так же B-2=B222, B′-2=B′222и C-3=C232, C′-3=C′232. Соединяя точки А,В,Си А′, В′, С′, получаем развертку боковой поверхности призмы. Присоединяя к развертке боковой поверхности призмы оба основания (треугольни-ки АВСи А′В′С′), получаем полную развертку призмы (см. рис. 13.2, б). На развертку призмы нанесена точка К, принадлежащая грани АВВ′А′. Для построения на развертке точки Kиспользована вспомогательная прямая EE′, проходящая через точку Kи парал-лельная ребрам призмы. 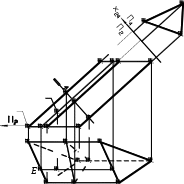 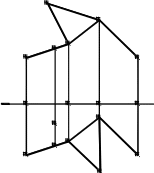 14 24 A′ C′ 14 24 A′ C′34 A′2 E′2 A′ Σ2B′2C′2 E′ B′ A′ K212A2  E2 B2A111 E2 B2A111 K′11 K′1122 32C2 A′1 C131  E′1 E′1Σ 1 2 3 1 C K C′1 A EB A A B1 21 B′1 а) б) Рис. 13.2 Кроме способа нормального сечения, для построения развертки поверхности приз-мы может быть использован способраскатки(частный случай способа нормальных сечений) или способтриангуляции, когда каждая грань призмы делится диагональю на два треугольника [6]. |
