лекция. Лекция 13. Развертки поверхностей
 Скачать 1.4 Mb. Скачать 1.4 Mb.
|
|
Рис. 13.8 Считая, что пирамида не усечена, построим ее развертку. Развертка каждой грани представляет собой треугольник, боковые стороны которого равны длинам соответст-вующих ребер неусеченной пирамиды (они определены на рис. 13.8, б), а длина осно-вания равна длине стороны 8-угольника, вписанного в круговое основание конуса. Раз-вертка поверхности неусеченной пирамиды представляет собой 8 примыкающих друг к другу треугольников с общей вершиной S (рис. 13.8, в). Пирамида усечена плоскостью, параллельной ее основанию, поэтому истинная фор-ма каждой грани усеченной пирамиды – трапеция. Развертка поверхности усеченной пирамиды представляет собой примыкающие друг к другу трапеции. Отложим на раз-вертке неусеченной пирамиды истинную длину какого-нибудь ребра усеченной пира-миды (например, длину ребра BC, изображенного на П2в натуральную величину). Че-рез точку Cна развертке проводим отрезок C-4, параллельный отрезку B-3. Затем из точки 4проводим отрезок 4-5, параллельный отрезку 3-2. Продолжая построение, по-лучаем развертку усеченной пирамиды в виде набора из восьми примыкающих друг к другу трапеций (см. рис. 13.8, в). Развертки нижнего и верхнего оснований усеченной пирамиды (не показанные на чертеже), имеют форму правильных 8-угольников, вписанных в нижнее и верхнее кру-говые основания данного усеченного конуса. 13.2.6. Приближенная развертка поверхности наклонного цилиндра Дан наклонный цилиндр с круговым основанием (рис. 13.9, а). Вписываем в ци-линдр 8-угольную наклонную призму (рис. 13.9, б). Точную развертку поверхности призмы будем считать приближенной разверткой поверхности наклонного цилиндра. 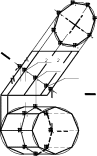  Г2 A′2 Г2 A′272 64 74 84 14 24 6=8 12=5222=42 54 44 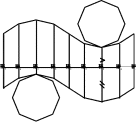 34 34A′ A2 32 Г 1 2 351 4 5 6 178 A1 71 61 41 31 A 81 21 11 а) б) в) Рис. 13.9 Развертку боковой поверхности призмы получают способом нормального сечения, в соответствии с которым боковую поверхность призмы рассекают фронтально-проецирующей плоскостью Г, перпендикулярной ее боковым ребрам (см. п. 13.1.2). Ис-тинная форма нормального сечения призмы 1424…84определена способом замены плоскостей проекций. Нормальное сечение 1424…84“разворачиваем” в прямую 1-2-…-8-1и через каждую точку проводим прямую, перпендикулярную линии нормального сечения (рис. 13.9, в). На каждом из построенных перпендикуляров откладываем отрез-ки боковых ребер, измеренные на П2до и после нормального сечения. Например, от-резки A-7и A′-7на развертке равны отрезкам A272и A′272на плоскости П2. Концы от-резков соединяем ломаными линиями. К развертке боковой поверхности призмы до-бавляем ее основания – два многоугольника (см. рис. 13.9, в). 13.3. Построение условных разверток неразвертывающихся поверхностей Многие сооружения часто ограничены неразвертывающимися поверхностями. Ме-жду тем условия их постройки заставляют изготавливать эти поверхности из листового материала. Поэтому составление условных разверток неразвертывающихся поверхно-стей представляет собой важную техническую задачу. Например, поверхность корпуса морского судна составляется из отсеков криволинейных поверхностей, которые вы-краивают из металлических листов, а затем склепывают друг с другом. Образуется кри-вая (а в сущности – многогранная) поверхность корпуса. Пусть требуется построить условную развертку некоторой неразвертывающейся поверхности Ф. Разбиваем поверхность Фна отдельные участки (отсеки). Каждый от-сек аппроксимируем (приближенно заменяем) отсеком какой-либо развертывающейся поверхности – многогранником, цилиндром или конусом (в зависимости от формы дан- ной поверхности Ф). В результате вместо исходной неразвертывающейся поверхности получаем поверхность Ф′, состоящую из участков развертывающихся поверхностей. Выполняем построение разверток всех участков составной поверхности Ф′. Совокуп-ность полученных разверток принимаем за условную развертку поверхности Ф. 13.3.1. Построение условных разверток способом триангуляции Напомним, что триангуляцией называют замену (аппроксимацию) данной поверх-ности многогранной поверхностью, состоящей из треугольных граней. Произвольная неразвертывающаяся поверхность Фможет быть аппроксимирована многогранной по-верхностью Ф′с треугольными гранями. Развертка полученной многогранной поверх-ности Ф′ принимается за условную развертку данной поверхности Ф. Пусть требуется построить условную развертку косой плоскости, “натянутой” на пространственный (неплоский) четырехугольник ABCD(рис. 13.10). Косая плоскость (гиперболический параболоид) – неразвертывающаяся поверхность, образованная пря-молинейной образующей, движущейся параллельно заданной плоскости параллелизма и пересекающей прямолинейные направляющие (см. п. 6.2.4). В рассматриваемом при-мере направляющие прямые – скрещивающиеся стороны ADи BCчетырехугольника ABCD, а плоскость П1– плоскость параллелизма. Горизонтальная образующая скользит по направляющим AD и BC, последовательно занимая положения AB, 1-1′, 2-2′, DC.  |C-2| |D-2| |C-2| |D-2|n A2 |C-2′| 1222 Δz ml D2 A111 m 21 D1 n  B2 B21′22′2 C2 |D-2| D B1C1 2′11′1 A 1 B 1′ 2 2′ C |C-2′| |C-2| |
