лекция. Лекция 13. Развертки поверхностей
 Скачать 1.4 Mb. Скачать 1.4 Mb.
|
|
Рис. 13.10 Чтобы выполнить триангуляцию, предварительно разбиваем отсек ABCDкосой плоскости на части с помощью образующих. Для упрощения построений поверхность разбита образующими AB, 1-1′, 2-2′, DCтолько на три части, каждая из которых огра-ничена пространственным четырехугольником. Проводя диагонали полученных неплоских четырехугольников, заменяем каждую часть поверхности двумя треугольниками. Например, нижний участок, ограниченный пространственным четырехугольником D-2-2′-C, заменен двумя треугольниками D2Cи C22′. В результате заданный отсек ABCDкосой плоскости заменен (аппроксимирован) многогранной поверхностью, состоящей из шести треугольников. При увеличении чис-ла разбиений точность аппроксимации возрастает. Для построения развертки полученной шестигранной поверхности надо определить истинные размеры сторон ее треугольных граней. На рис. 13.10 показано определение (способом прямоугольного треугольника) истинной величины отрезков D-2, C-2′и C-2. Для определения |D-2|построен вспомогательный прямоугольный треугольник с кате- тами Δzи m, где Δz– разность высот концов отрезка D-2, а m=D121– длина его гори-зонтальной проекции. Для определения |C-2′|построен прямоугольный треугольник с катетами Δzи l, где l=C12′1. Для определения |C-2|построен прямоугольный треуголь-ник с катетами Δzи n, где n=C121. Гипотенузы вспомогательных прямоугольных тре-угольников равны истинным величинам соответствующих отрезков. Истинные размеры остальных ребер аппроксимирующей многогранной поверхно-сти определяются аналогично (с учетом того, что горизонтальные отрезки AB, 1-1′, 2-2′, DCизображаются на П1в натуральную величину). После определения истинных раз-меров всех ребер выполняем построение развертки, состоящей из примыкающих друг к другу треугольников. Каждый из треугольников строится “по трем сторонам”. Полу-ченную точную развертку многогранной поверхности, состоящей из треугольных гра-ней, принимаем за условную развертку исходной неразвертывающейся поверхности. Примечание. Практически вся земная поверхность “покрыта” триангуляционной сетью опорных геодезических пунктов с таким расчетом, чтобы они являлись верши-нами треугольников, по возможности близких к равносторонним. В результате истин-ная поверхность земли аппроксимируется сетью треугольников (с размерами сторон на территории России 4…25 км). Геодезические пункты отмечаются заложенными в зем-лю бетонными пилонами, над которыми сооружаются вышки. Координаты каждого геодезического пункта (широта, долгота, высота над уровнем моря) определены с большой точностью. Сеть геодезических пунктов используется как для геодезических работ, так и в системах глобального позиционирования (GPS, ГЛОНАСС). 13.3.2. Построение условных разверток поверхностей вращения 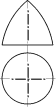 Для построения условных разверток неразвертывающихся поверхностей вращения за аппроксимирующие поверхности принимают цилиндры и конусы. В соответствии с этим различают два способа построения условных разверток поверхностей вращения: способ цилиндров и способконусов. Для построения условных разверток неразвертывающихся поверхностей вращения за аппроксимирующие поверхности принимают цилиндры и конусы. В соответствии с этим различают два способа построения условных разверток поверхностей вращения: способ цилиндров и способконусов. Пусть требуется построить условную развертку по-верхности вращения (рис. 13.11). При построении услов-ной развертки способомцилиндровданная поверхность мысленно разрезается меридиональными плоскостями Г, Г′,… (то есть плоскостями, проходящими через ее ось вращения), на несколько равных частей (рис. 13.12, а). Каждая часть заменяется отсеком цилиндрической по-верхности Ф, которая касается заданной поверхности вдоль ее меридиана m. В результате поверхность враще-ния приближенно заменяется (аппроксимируется) состав- Пусть требуется построить условную развертку по-верхности вращения (рис. 13.11). При построении услов-ной развертки способомцилиндровданная поверхность мысленно разрезается меридиональными плоскостями Г, Г′,… (то есть плоскостями, проходящими через ее ось вращения), на несколько равных частей (рис. 13.12, а). Каждая часть заменяется отсеком цилиндрической по-верхности Ф, которая касается заданной поверхности вдоль ее меридиана m. В результате поверхность враще-ния приближенно заменяется (аппроксимируется) состав-ной поверхностью, состоящей из одинаковых цилиндри- Рис. 13.11 ческих “лепестков” Фс горизонтальными образующими. Каждый лепесток можно приближенно развернуть на плоскость. Совокупность развер-ток всех лепестков составляет условную развертку поверхности вращения. При построении условной развертки поверхности вращения способомконусовдан-ная поверхность, как и при использовании способа цилиндров, мысленно разрезается на несколько частей. Но секущие плоскости Σ, Σ′,… проводят не через ось вращения, а перпендикулярно ей. Вся поверхность делится секущими плоскостями на несколько горизонтальных “поясков” (рис. 13.12, б). Каждый поясок заменяется отсеком кониче-ской поверхности Θ. В результате заданная поверхность вращения приближенно заме-няется (аппроксимируется) составной поверхностью, состоящей из разных конических поясков Θ, стыкующихся между собой по параллелям данной поверхности вращения. Каждый конический поясок, представляющий собой поверхность усеченного кругового конуса, можно развернуть на плоскость. Совокупность разверток всех поясков со-ставляет условную развертку поверхности.  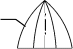 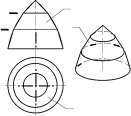 Ф2= m2 Σ2 Θ2Σ′2Θ Ф2= m2 Σ2 Θ2Σ′2Θ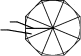  Г′1 Г′1Ф1m1 Ф  Г1 Г1Θ1 а) б) Рис. 13.12 Рассмотрим конструктивное построение условной развертки неразвертывающейся поверхности вращения способом цилиндров и способом конусов. 13.3.2.1. Способ цилиндров Данную поверхность вращения мысленно разрезаем меридиональными плоскостя-ми Г, Г′,… на равные участки (рис. 13.13, а). Развертки одинаковых участков поверхно- m2 D2 S2 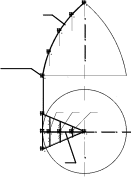 C2 C2B2 12=22=A2 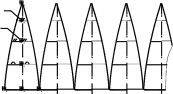 D S D SC B Г1′ 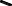 11 B1 11 B1A1 C1 D1 1 A 2 S1 |