лекция. Лекция 13. Развертки поверхностей
 Скачать 1.4 Mb. Скачать 1.4 Mb.
|
|
а) б) Рис. 13.13 сти одинаковы, поэтому достаточно построить условную развертку лишь одного участ-ка. На рис. 13.13, аповерхность разрезана на 8 участков. Показан только один участок, выделенный плоскостями Г, Г′. Отмечен средний меридиан m=AS этого участка. Заменим выделенный участок поверхности вращения участком (отсеком) Фцилин-дрической поверхности, касающейся заменяемого участка вдоль среднего меридиана m. Меридиан mрасположен во фронтальной плоскости уровня, поэтому дуга ASмеридиа-на m изображается на П2в натуральную величину. Цилиндрический отсек Ф, как и выделенный участок поверхности вращения, огра-ничен плоскостями Г, Г′. Поверхность отсека Фзанимает фронтально-проецирующее положение, поэтому его фронтальная проекция совпадает на чертеже с фронтальной проекцией m2меридиана m. Горизонтальная проекция отсека Ф – треугольник 1121S1. Таким образом, участок исходной поверхности вращения, ограниченный плоско-стями Г, Г′, приближенно заменяется (аппроксимируется) отсеком Фцилиндрической поверхности, ограниченным теми же плоскостями Г, Г′. Направляющая линия поверх-ности Ф– меридиан m, являющийся одновременно нормальным сечением цилиндра Ф; образующие цилиндра Ф горизонтальны (см. рис. 13.13, а). Для приближенного построения развертки отсека Фзаменяем направляющую m=ASломаной линией ABCDS, фронтальная проекция A2B2C2D2S2которой указывает истинную длину всех ее звеньев. В соответствии со способом нормального сечения, спрямляем ломаную линию A2B2C2D2S2в отрезок ABCDS, начерченный на свободном месте чертежа (рис. 13.13, б). Через точки A, B, C, Dпроводим прямые, перпендику-лярные AS, на которых откладываем отрезки касательных, проведенных к соответст-вующим параллелям. Эти отрезки ограничены плоскостями Г, Г′. Например, через точ-ку Aпроведен отрезок 1-2касательной к круговому основанию данного тела вращения, ограниченный плоскостями Г, Г′. Соединяя концы отрезков касательных плавной кривой, получаем приближенную развертку одного цилиндрического “лепестка” 1-2-S. Полная условная развертка дан-ной поверхности вращения состоит из восьми таких лепестков (см. рис. 13.13, б). Точ-ность построения условной развертки увеличивается с увеличением числа участков, на которые разделена данная поверхность. 13.3.2.2. Способ конусов Данную поверхность вращения мысленно разрезаем плоскостями, перпендикуляр-ными ее оси, на несколько частей – “поясков”. Для упрощения построений поверхность разрезана плоскостями Δ, Δ′всего на три части (рис. 13.14, а). Меридиан ASданной по-верхности вращения заменяем ломаной линией ABCS, что позволяет аппроксимировать “пояски” отсеками конических поверхностей вращения, образующие которых совпада-ют со звеньями ломаной линии ABCS. Верхний участок поверхности (от вершины Sдо параллели c) заменен конической поверхностью с вершиной Sи образующей CS. Сред-ний участок (между параллелями bи c) заменен отсеком поверхности усеченного кону-са с образующей BCи вершиной S′. Нижний участок (от основания aдо параллели b) заменяется отсеком поверхности усеченного конуса с образующей ABи вершиной S′′. Все отсеки конических поверхностей имеют общую ось вращения, совпадающую с осью данной поверхности. После аппроксимации данной поверхности вращения тремя отсеками конических поверхностей построение условной развертки сводится к построению разверток по-верхностей трех конусов. Построение этих разверток, показанное на рис. 13.14, б, вы-полняется точно (см. п. 13.2.1). Например, развертка нижнего отсека конической по-верхности (с направляющей a, образующей ABи вершиной S′′) представляет собой часть сектора, ограниченного двумя концентрическими дугами окружностей с радиу-сами |AS′′|и |BS′′|. Центральный угол сектора вычисляется по формуле α=360°r/l, где l=|AS′′|, r – радиус параллели a. Длины дуг окружностей, соприкасающихся в точках B, C, равны между собой, так как они соответствуют параллелям b, c данной поверхности. Совокупность разверток отсеков конических поверхностей, показанная на рис. 13.14, б, принимается за условную развертку данной неразвертывающейся поверхности вращения. Точность построения условной развертки увеличивается с увеличением чис-ла участков, на которые разделена данная поверхность. 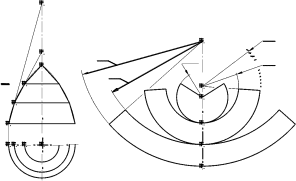 S2′′ S2′′S2′ |AS′′| S2  Δ2′ c2 |BS′′| Δ2 B2C2b2 Δ2′ c2 |BS′′| Δ2 B2C2b2S′′ |BS′| |CS| |CS′| S′ c S A2 a2 b C B1C1 S1 A1 c1b1 a1 a B A а) б) Рис. 13.14 |
