реферат. Реферат молекулярная физика и термодинамика проверил москва 2017
 Скачать 0.99 Mb. Скачать 0.99 Mb.
|
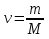 на постоянную Авогадро NA. на постоянную Авогадро NA.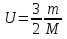 RT RT Внутренняя энергия идеального газа прямо пропорциональна его абсолютной температуре. От объема газа она не зависит. Внутренняя энергия газа представляет собой среднюю кинетическую энергию всех его атомов. Если центр масс газа движется со скоростью v0, то полная энергия газа равна сумме механической (кинетической) энергии и внутренней энергии: 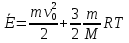 4.2. Первое начало термодинамики Первое начало термодинамики - один из трех основных законов термодинамики, представляющий собой закон сохранения энергии для систем, в которых существенное значение имеют тепловые процессы. Согласно первому началу термодинамики, термодинамическая система (например, пар в тепловой машине) может совершать работу только за счёт своей внутренней энергии или каких-либо внешних источников энергии. Суть первого начала термодинамики заключается в следующем: При сообщении термодинамической системе некоторой теплоты Q происходит изменение внутренней энергии системы ΔU и система совершает работу А: Q = ΔU + A Данная формула, выражающая первое начало термодинамики, является определением изменения внутренней энергии системы (ΔU), так как Q и А — независимые величины. Внутреннюю энергию системы U можно найти, измеряя работу системы в адиабатном процессе (Q = 0): А = — ΔU Первое начало термодинамики утверждает, что U является функцией состояния системы, то есть каждое состояние термодинамической системы характеризуется определённым значением U, независимо от того, каким путём система приведена в данное состояние. 4.3. Теплоемкость (удельная и молярная). Удельная теплоемкость вещества - физическая величина, численно равная количеству энергии в форме теплоты, которое надо сообщить единице массы этого вещества для увеличения его температуры на 1 Кельвин 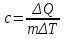 ,[c]= Дж/(кг*К) ,[c]= Дж/(кг*К)Удельная теплоемкость зависит от рода вещества и от вида термодинамического процесса, в котором телу сообщается количество теплоты. Количество теплоты, поглощённой телом при изменении его состояния, зависит не только от начального и конечного состояний, но и от способа, которым был осуществлен процесс перехода между ними. Поэтому для газов различают два вида теплоемкостей: если газ нагревают, сохраняя его объем постоянным, говорят об удельной теплоемкости газа при постоянном объеме cV; если же газ нагревают, сохраняя постоянным его давление, то говорят об удельной теплоемкости газа при постоянном давлении сР. У жидкостей и твёрдых тел разница между Ср и Cv мала. Часто пользуются молярной теплоемкостью Сμ, которая, в отличие от удельной теплоемкости, отнесена не к единице массы, а к массе одного моля вещества. Очевидно, что 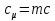 , [c]=Дж/(моль*К) , [c]=Дж/(моль*К)Для газов молярную теплоемкость, рассчитанную при постоянном давлении, обозначают СР, а рассчитанную при постоянном объеме – СV. Следовательно, 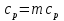 , , 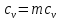 . .Когда нагревание газа происходит при постоянном объеме, газ не совершает механической работы и все сообщаемое газу тепло идет только на увеличение его внутренней энергии ΔU, т.е.: 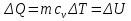 . .Если же нагревание газа происходит при постоянном давлении и, следовательно, объем газа увеличивается, то сообщаемое газу тепло ΔQ идет как на увеличение его внутренней энергии ΔU, так и на совершение газом работы ΔA над внешними телами, т.е. 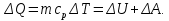 Из сопоставления формул следует, что cP > cV, т.е. удельная теплоемкость газа при постоянном давлении больше удельной теплоемкости того же газа при постоянном объеме. 4.4. Изопроцессы Изопроцессы — термодинамические процессы, во время которых количество вещества и один из параметров состояния: давление, объём или температура — остаются неизменными. Так, неизменному давлению соответствует изобарный процесс, объёму — изохорный, температуре — изотермический. Линии, изображающие данные процессы на какой-либо термодинамической диаграмме, называются изобара, изохора, изотерма. Изобарный процесс Изобарный процесс — процесс изменения состояния термодинамической системы при постоянном давлении(p=const) 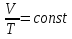 -Закон Гей-Люссака. -Закон Гей-Люссака.Изохорный процесс Изохорный процесс — процесс изменения состояния термодинамической системы при постоянном объёме ( 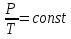 Изотермический процесс Изотермический— процесс изменения состояния термодинамической системы при постоянной температуре ( 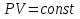 - законом Бойля — Мариотта: - законом Бойля — Мариотта: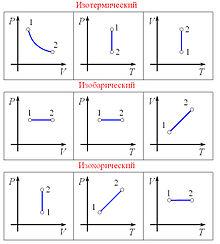 4.5.Адиабатический процесс, уравнение Пуассона. Адиабатический процесс - это такое изменение состояний газа, при котором он не отдает и не поглощает извне теплоты. Следовательно, адиабатический процесс характеризуется отсутствием теплообмена газа с окружающей средой. Адиабатическими можно считать быстро протекающие процессы. Так как передачи теплоты при адиабатическом процессе не происходит, то 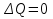 и уравнение I начала термодинамики принимает вид и уравнение I начала термодинамики принимает видили 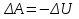 т.е. внешняя работа газа может производиться вследствие изменения его внутренней энергии. Адиабатное расширение газа (dV>0) сопровождается положительной внешней работой, но при этом внутренняя энергия уменьшается и газ охлаждается (dT<0). 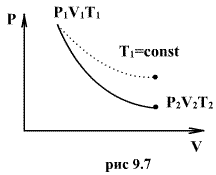 Уравнение Пуассона описывает адиабатный процесс, протекающий в идеальном газе. Уравнение Пуассона имеет вид: 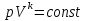 Здесь V-объем, занимаемый газом, p – его давление, а величина k- показателть адиабаты. Показатель адиабаты в уравнении Пуассона Показатель адиабаты можно рассчитать, как отношение изобарной теплоемкости газа к его изохорной теплоемкости: 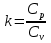 В практических расчётах удобно помнить, что для идеального газа показатель адиабаты равен 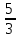 , для двухатомного – , для двухатомного – 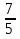 , а для трёхатомного – , а для трёхатомного – 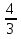 . .Показатель адиабаты всегда больше 1, поэтому при адиабатическом сжатии газа – как идеального, так и реального – до меньшего объема температура газа всегда возрастает, а при расширении газ охлаждается. Это свойство адиабатического процесса, называемое пневматическим огнивом, применяется в дизельных двигателях, где горючая смесь сжимается в цилиндре и воспламеняется от высокой температуры. Вспомним первый закон термодинамики: 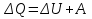 , где ΔU — внутренняя энергия системы, а А – выполняемая над ней работа. Поскольку , где ΔU — внутренняя энергия системы, а А – выполняемая над ней работа. Поскольку 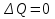 то работа, осуществляемая газом, идёт только на изменение его внутренней энергии – а значит, температуры. Из уравнения Пуассона можно получить формулу для расчёта работы газа в адиабатном процессе: то работа, осуществляемая газом, идёт только на изменение его внутренней энергии – а значит, температуры. Из уравнения Пуассона можно получить формулу для расчёта работы газа в адиабатном процессе: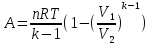 Здесь n – количество газа в молях, R – универсальная газовая постоянная, Т – абсолютная температура газа. 4.6. Работа, совершаемая газом при различных процессах Внутренняя энергия газа может изменяться в результате совершения газом работы и сообщения ему теплоты. Работа газа при произвольном процессе рассчитывается как площадь криволинейной трапеции под графиком p(V). На рисунке показана произвольная зависимость давления газа p от его объема V. Площадь заштрихованной фигуры совпадает с работой, совершенной газом. 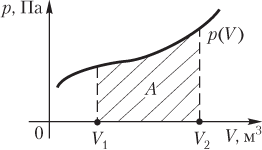 В Международной системе единиц работа, совершаемая газом, измеряется в джоулях (1 Дж). Работа газа при изобарном процессе (p = const) может быть вычислена по одной из формул: A = p∆V, или A = νR∆T, где p — давление газа; ΔV — изменение объема газа. ν — количество вещества (газа); R — универсальная газовая постоянная, R ≈ 8,31 Дж/(моль ⋅ К); ΔT — соответствующее изменение температуры газа. Работа газа при изохорном процессе (V = const) не совершается: A = 0. Работа газа при круговом (циклическом) процессе рассчитывается как площадь фигуры, ограниченной графиком функции p(V). Ниже показан график произвольного кругового процесса; цифрами обозначены: 1 — исходное состояние идеального газа (оно совпадает с конечным); 2, 3 — промежуточные состояния газа. 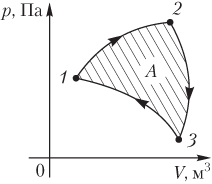 Площадь заштрихованной фигуры совпадает с работой, совершенной газом при циклическом процессе. Работа, совершаемая газом за цикл, может быть: · положительной (прямой цикл); · отрицательной (обратный цикл). 5.1. Реальные газы и 5.2. Уравнение Ван-дер-Ваальса. Реальные газы имею место вблизи точки конденсации (при высоком давлении и низкой температуре). Их свойства значительно отличается от свойств идеального газа. Уравнение состояния для 1-го моля идеального газа 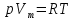 ( 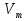 – молярный объем) видоизменяется в случае реальных газов. – молярный объем) видоизменяется в случае реальных газов.Для реальных газов необходим учет собственного объема молекул. Наличие сил отталкивания, которые противодействуют проникновению в занятый молекулой объем других молекул, сводится к тому, что фактический свободный объем, в котором могут двигаться молекулы реального газа, будет не Vm, а Vm – b, b – объем, занимаемый самими молекулами. Объем b равен учетверенному собственному объему молекул. Действие сил притяжения газа приводит к появлению дополнительного давления на газ, называемого внутренним давлением. По вычислениям Ван-дер-Ваальса, внутреннее давление обратно пропорционально квадрату молярного объема, т. е. 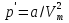 , ,где a – постоянная Ван-дер-Ваальса, характеризующая силы межмолекулярного притяжения. Вводя поправки в уравнение 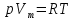 для идеального газа, получим уравнение Ван-дер-Ваальса для 1-го моля газа для идеального газа, получим уравнение Ван-дер-Ваальса для 1-го моля газа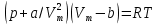 . .Учитывая, что 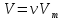 (ν=m/μ), получим уравнение для произвольного количества вещества: (ν=m/μ), получим уравнение для произвольного количества вещества: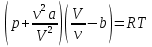 Поправки Ван-дер-Ваальса (a и b) являются постоянными для каждого газа величинами. Для их определения записывают уравнения для двух известных из опыта состояний газа и решаются относительно a и b. 5.3. Энтропия. Важнейшим параметром состояния вещества является энтропия (S, [S]= Дж/К.). Изменение энтропии в обратимом термодинамическом процессе определяется уравнением, являющимся аналитическим выражением второго закона термодинамики: 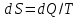 для 1 кг вещества — 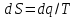 , где dq — бесконечно малое количество теплоты, подводимой или отводимой в элементарном процессе при температуре Т, кДж / кг. , где dq — бесконечно малое количество теплоты, подводимой или отводимой в элементарном процессе при температуре Т, кДж / кг.Энтропия характеризует степень вариативности микросостояния объекта. Чем выше энтропия, тем в большем числе существенно различных микросостояний может находиться объект при данном макросостоянии. Энтропия — это свойство системы, которое полностью определяется состоянием системы. Какими бы путями не перешла система из одного состояния в другое, изменение её энтропии будет всегда одно и тоже. Вычислить можно только изменение энтропии при переходе системы из одного состояния в другое. Уравнение Клаузиуса: 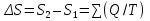 обратимый обратимыйИзменение энтропии при переходе системы из одного состояния в другое точно равно сумме приведенных теплот. Энтропия — мера статистического беспорядка в замкнутой термодинамической системе. Чем больше порядка — тем меньше энтропия. И наоборот, чем меньше порядка — тем больше энтропия. Все самопроизвольно протекающие процессы в замкнутой системе, приближающие систему к состоянию равновесия и сопровождающиеся ростом энтропии, направлены в сторону увеличения вероятности состояния. Энтропия является функцией состояния, поэтому её изменение в термодинамическом процессе определяется только начальными и конечными значениями параметров состояния. Изменение энтропии в основных термодинамических процессах определяется: В изохорном dЅv = Сv lnТ2/Т1 В изобарном dЅр = Ср lnТ2/Т1 В изотермическом dЅт = RlnР1/Р2 = RlnV2/V1 5.4. Энтропия и термодинамическая вероятность системы. Больцман показал, что смысл энтропии носит статистический (вероятностный) характер. S = klnW, где k – коэффициент пропорциональности, называемый постоянной Больцмана ( 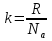 = 8,314 / 6,021023 1,3810–23 Дж/К ), = 8,314 / 6,021023 1,3810–23 Дж/К ),W – термодинамическая вероятность данного состояния системы. Чем больше неупорядоченность системы, тем система более вероятна, и тем ее энтропия больше. Иными словами, можно сказать, что энтропия – это мера хаоса. Второй закон термодинамики имеет ограниченный (статистический) характер, поскольку он применим к системам, состоящим из большого числа частиц. 5.5. Равновесные процессы. В равновесном процессе силы, действующие на систему, почти точно уравновешиваются другими силами со стороны системы. Отсюда ясно, что если снять движущие воздействия, процесс прекратится. Если же изменить знак воздействий, начнется обратный процесс. Отсюда следует, равновесному процессу присуща двусторонность. Ещё одна отличительная черта равновесного процесса — отсутствие потерь энергии на преодоление трения, завихрений потоков в газах и жидкостях. Следовательно, работа, совершаемая системой против внешней среды в равновесном процессе, максимально возможная. Энергия же, рассеянная в виде теплоты, минимальна. Расширение газа в цилиндре с поршнем хорошо иллюстрирует различие между равновесным и неравновесным процессами. 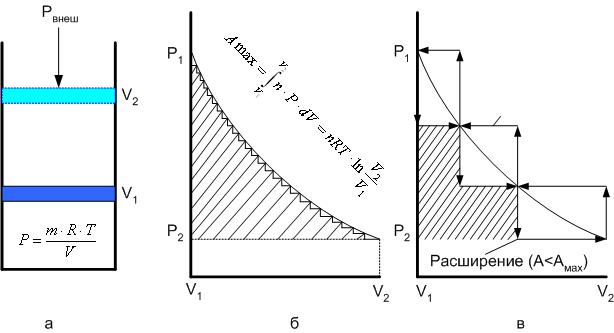 Поршень в представленном на рисунке цилиндре не движется, если давление п молей газа в объеме V1 уравновешено внешним давлением Р (например, Р — это вес поршня и набора гирь с разным весом). Пусть вся система погружена в термостат. Чтобы вызвать медленное расширение газа до конечного объема V2, надо поочередно снимать самые маленькие гирьки, например, весом 1 г. Каждый раз после снятия гирьки давление газа будет слегка превышать внешнее давление; расширение газа прекращается, когда внешнее давление уравновешивается внутренним давлением, которое для идеального газа равно 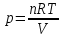 На графике этот процесс изображен ступеньками (вертикальная черточка — снятие груза, горизонтальная — расширение до равновесного объема). В данном случае процесс еще не является вполне равновесным, так как изменение уравновешивающего давления происходит, хотя и с малой, но конечной скоростью. Если же снимать груз бесконечно малыми порциями, давление газ каждый раз будет бесконечно мало превышать внешнее давление, и расширение станет вполне равновесным. В таком случае на графике P-Vнадо вместо ступеньки изображать ее бесконечно малую форму, т. е точку, а весь процесс представить непрерывным рядом точек, т. е кривой На графике этот процесс изображен ступеньками (вертикальная черточка — снятие груза, горизонтальная — расширение до равновесного объема). В данном случае процесс еще не является вполне равновесным, так как изменение уравновешивающего давления происходит, хотя и с малой, но конечной скоростью. Если же снимать груз бесконечно малыми порциями, давление газ каждый раз будет бесконечно мало превышать внешнее давление, и расширение станет вполне равновесным. В таком случае на графике P-Vнадо вместо ступеньки изображать ее бесконечно малую форму, т. е точку, а весь процесс представить непрерывным рядом точек, т. е кривой К разновидностям равновесных процессов относятся термодинамически обратимые процессы |
