реферат. Реферат молекулярная физика и термодинамика проверил москва 2017
 Скачать 0.99 Mb. Скачать 0.99 Mb.
|
|
, которые могут идти как в прямом, так и в обратном направлениях при бесконечно малом изменении действующих на систему сил без изменения работоспособности системы в обоих направлениях. Таким образом, обратимые процессы должны протекать бесконечно медленно, через одну и ту же непрерывную последовательность состояний равновесия в обоих направлениях и так, чтобы после возвращения системы в первоначальное состояние ни в окружающей среде, ни в самой системе не осталось никаких изменений. 5.6. Обратимые процессы. Термодинамический процесс называется обратимым, если он может происходить как в прямом, так и в обратном направлении, причем если такой процесс происходит сначала в прямом, а затем в обратном направлении и система возвращается в исходное состояние, то в окружающей среде и в этой системе не происходит никаких изменений. Любой равновесный процесс является обратимым. Обратимость равновесного процесса, происходящего в системе, следует из того, что ее любое промежуточное состояние есть состояние термодинамического равновесия; независимо от того идет ли процесс в прямом или в обратном направлении. Реальные процессы сопровождаются рассеянием, которая нами не рассматривается. Обратимые процессы – это идеализация реальных процессов. Их рассмотрение важно по 2-м причинам: 1) многие процессы в природе и технике практически обратимы; 2) обратимые процессы являются наиболее экономичными; имеют максимальный термический коэффициент полезного действия, что позволяет указать пути повышения КПД реальных тепловых двигателей. 5.7. Циклы. Термодинамические циклы —процессы, в которых начальные и конечные параметры, определяющие состояние рабочего тела совпадают. Термодинамические циклы являются моделями процессов, происходящих в реальных тепловых машинах для превращения тепла в механическую работу. Любая тепловая машина состоит из рабочего тела, нагревателя и холодильника. Обратимым называют цикл, который можно провести как в прямом, так и в обратном направлении в замкнутой системе. Суммарная энтропия системы при прохождении такого цикла не меняется. Единственным обратимым циклом для машины, в которой передача тепла осуществляется только между рабочим телом, нагревателем и холодильником, является Цикл Карно. Существуют также другие циклы, в которых обратимость достигается путём введения дополнительного теплового резервуара — регенератора. Основные принципы. Холодильник и нагреватель управляют состоянием рабочего тела. В каждом цикле рабочее тело забирает некоторое количество теплоты ( 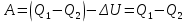 , ,так как изменение внутренней энергии в круговом процессе равно нулю. При этом нагреватель потратил энергию 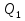 . Поэтому тепловой коэффициент полезного действия тепловой машины равен . Поэтому тепловой коэффициент полезного действия тепловой машины равен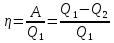 . .Работа в термодинамическом цикле, по определению, равна где C другой стороны, в соответствии с первым началом термодинамики, можно записать Аналогично, количество теплоты, переданное нагревателем рабочему телу, равно Наиболее удобными параметрами для описания состояния рабочего тела в термодинамическом цикле служат температура и энтропия.. 6.1. Второе начало термодинамики. Второе начало термодинамики описывается процессами, происходящими в замкнутой системе, в итоге которых энтропия не убывает. Речь идет о замкнутых системах, так как в незамкнутых системах энтропия может вести себя любым образом. Кроме того, отметим еще раз, что энтропия остается постоянной в замкнутой системе только при обратимых процессах. При необратимых процессах в замкнутой системе энтропия всегда возрастает. Формула Больцмана позволяет дать статистическое толкование второго начала термодинамики. Оно, являясь статистическим законом, описывает закономерности хаотического движения большого числа частиц, составляющих замкнутую систему. У второго начала термодинамики есть ещё 2 формулировки: 1) по Кельвину: невозможен круговой процесс, единственным результатом которого является превращение теплоты, полученной от нагревателя, в эквивалентную ей работу; 2) по Клаузиусу: невозможен круговой процесс, единственным результатом которого является передача теплоты от менее нагретого тела к более нагретому. 6.2. К.П.Д. тепловой машины. Тепловой двигатель тем эффективнее, чем выше температура нагревателя и ниже температура холодильника. Но температура холодильника практически не может быть намного ниже температуры окружающего воздуха. Повышать температуру нагревателя можно. Однако любой материал (твердое тело) обладает ограниченной теплостойкостью, или жаропрочностью. При нагревании он постепенно утрачивает свои упругие свойства, а при достаточно высокой температуре плавится. Коэффициент полезного действия любого теплового двигателя не может превышать максимально возможного значения 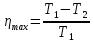 , где , где 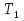 —абсолютная температура нагревателя, а —абсолютная температура нагревателя, а 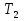 — абсолютная температура холодильника. — абсолютная температура холодильника.6.3. Цикл Карно и 6.4. К.П.Д. цикла Карно. Фаза А→Б. Рабочее тело с температурой, равной температуре нагревателя, приводится в контакт с нагревателем. Нагреватель сообщает рабочему телу 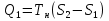 тепла в изотермическом процессе, при этом объём рабочего тела увеличивается. тепла в изотермическом процессе, при этом объём рабочего тела увеличивается.Фаза Б→В. Рабочее тело отсоединяется от нагревателя и продолжает расширяться адиабатически. При этом его температура уменьшается до температуры холодильника. Фаза В→Г. Рабочее тело приводится в контакт с холодильником и передает ему 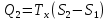 тепла в изотермическом процессе. При этом объём рабочего тела уменьшается. тепла в изотермическом процессе. При этом объём рабочего тела уменьшается.Фаза Г→А. Рабочее тело адиабатически сжимается до исходного размера, и его температура увеличивается до температуры нагревателя. Его КПД равен, таким образом, 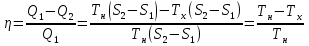 , ,то есть, зависит только от температур холодильника и нагревателя. Видно, что 100%-ный КПД можно получить только в том случае, если температура холодильника есть абсолютный нуль, что недостижимо. Никакая тепловая машина с теми же температурами нагревателя и холодильника не может обладать большим КПД. Заметим, что мощность тепловой машины Карно равна нулю, так как передача тепла в отсутствие разности температур идёт бесконечно медленно. 6.5. Система с изменяющимся числом частиц, химический потенциал. Термодинамика рассматривает системы, состоящие из нескольких компонент с переменным составом, который изменяется в зависимости от температуры и давления. Если в системе изменяется число частиц, то изменение ее внутренней энергии зависит не только от теплообмена и совершения работы, но и связано с изменением числа частиц в системе. Если в системе несколько компонентов, то ее внутренняя энергия зависит от концентрации ( 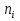 ) каждой компоненты. Если в качестве независимых переменных взять объем (V) и энтропию (S), то U=U(S,V, ) каждой компоненты. Если в качестве независимых переменных взять объем (V) и энтропию (S), то U=U(S,V,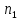 , ,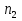 ,…, ,…,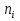 ). ). В таком случае можно записать: если где суммирование производится по всем 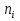 , а при взятии частной производной по , а при взятии частной производной по 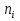 остальные остальные 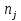 ≠ ≠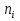 считаются постоянными. Для однокомпонентной системы справедливо уравнение, где считаются постоянными. Для однокомпонентной системы справедливо уравнение, где 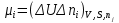 , , 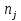 ≠ ≠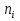 - химический потенциал. Аналогично можно модифицировать остальные термодинамические функции с учетом числа частиц. - химический потенциал. Аналогично можно модифицировать остальные термодинамические функции с учетом числа частиц. Надо считать, что функция Гиббса (Ф) зависит от давления (p), температуры (T) и концентрации частиц компонент ( 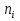 ). Окончательно формула для элемента функции Гиббса с учетом изменения числа частиц в системе примет вид: где ). Окончательно формула для элемента функции Гиббса с учетом изменения числа частиц в системе примет вид: где 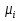 = =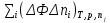 . Функция Гиббса пропорциональна числу n. Поэтому можно записать, что: где химический потенциал однокомпонентной фазы равен среднему значению функции Гиббса, который приходится на одну молекулу. μi - химический потенциал. Химический потенциал для каждой компоненты имеет одно и тоже значение во всех фазах, в условии равновесия, при постоянных температуре и давлении. . Функция Гиббса пропорциональна числу n. Поэтому можно записать, что: где химический потенциал однокомпонентной фазы равен среднему значению функции Гиббса, который приходится на одну молекулу. μi - химический потенциал. Химический потенциал для каждой компоненты имеет одно и тоже значение во всех фазах, в условии равновесия, при постоянных температуре и давлении.7.1. Диффузия. Диффузия представляет собой процесс, когда смесь переходит из области с высокой концентрацией в области низкой концентрацией. Причиной этого является перемещение атомов и молекул. Обычно причиной служит тепло, под воздействием которого весь процесс и происходит. Заканчивается он тогда, когда градиент концентрации кончается. Диффузия газов и жидкостей происходит быстро, что нельзя сказать о твердых веществах. Это легко заметно в обычной жизни, ведь нагреть воду гораздо быстрее, чем растопить пластмассу. Синтетические материалы подвержены слабой диффузии, а металлические наоборот. Диффузировать могут частицы, которые всегда находятся в веществе. Также этому процессу поддаются и посторонние вещества. Чтобы диффузия произошла в газах и жидкостях необходимо применить броуновское движение. Оно представляет собой движение молекул под воздействием высоких температур. Для того чтобы вызвать диффузию твердых веществ можно использовать диффузный насос. В нем есть масло, которое нагревается и поднимается вверх, а там уже происходит откачивание. Пары в это время проходят вверх и по специальным каналам насоса опускаются вниз для охлаждения. По пути они захватывают газы и уносят их с собой. Пар конденсируется и стекает в специальную емкость. Все это позволяет добиваться минимального давления. Диффузия может быть: коллоидная; конвективная; квантовая; турбулентная. Первый вид диффузии представляет собой процесс, который происходит в твердых телах. Турбулентная — это перенос мельчайших частиц в потоке турбулентности. Квантовая диффузия отмечается там, где очень низкие температуры и присутствует конденсат. Конвективная диффузия происходит, когда частицы двигаются в среде, которая тоже двигается с особой скоростью. Нередко можно наблюдать, как к диффузии относят явления, во время которых не переносятся частицы. Например, в оптике можно встретить процесс переноса излучения в среде, которая отличается неоднородностью. Это процесс должен сопровождаться поглощением фотонов, что и называют диффузией. 7.2. Теплопроводность. Теплопроводность — это перенос теплоты структурными частицами вещества в процессе их теплового движения. Такой теплообмен может происходить в любых телах с неоднородным распределением температур, но механизм переноса теплоты будет зависеть от агрегатного состояния вещества. Явление теплопроводности заключается в том, что кинетическая энергия атомов и молекул, которая определяет температуру тела, передаётся другому телу при их взаимодействии или передаётся из более нагретых областей тела к менее нагретым областям. Иногда теплопроводностью называется также количественная оценка способности конкретного вещества проводить тепло. Явление теплопроводности обусловлено стремлением занять состояние более близкое к термодинамическому равновесию, что выражается в выравнивании температуры. В установившемся режиме поток энергии, передающейся посредством теплопроводности, пропорционален градиенту температуры: 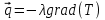 , ,где В интегральной форме это же выражение запишется так (если речь идёт о стационарном потоке тепла от одной грани параллелепипеда к другой): 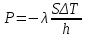 , ,где 7.3. Вязкость. Вязкость– свойство текучих тел оказывать сопротивление перемещению одной их части относительно другой. Жидкости, вязкость которых не зависит от напряжения сдвига и при определенной концентрации и температуре является постоянной величиной в соответствии с законом Ньютона, называются ньютоновскими. Неньютоновские жидкости не следуют закону Ньютона, их вязкость зависит от напряжения сдвига. Различают динамическую, кинематическую, относительную, удельную, приведенную и характеристическую вязкости. Для неньютоновских жидкостей, главным образом, характерна структурная вязкость. Структурная вязкость – вязкость при данном напряжении сдвига. Динамическая вязкость или коэффициент вязкости (η)– это приходящаяся на единицу поверхности тангенциальная сила, называемая также напряжением сдвига (τ),выраженная в паскалях (Па), которую необходимо приложить для того, чтобы переместить слой жидкости площадью 1 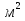 со скоростью (v) 1 м/с, находящийся на расстоянии (х) 1 м относительно другого слоя, параллельно плоскости скольжения. со скоростью (v) 1 м/с, находящийся на расстоянии (х) 1 м относительно другого слоя, параллельно плоскости скольжения.Величина dv/dx представляет собой градиент скорости и определяет скорость сдвига D, выраженную в обратных секундах ( 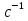 ). Таким образом, ). Таким образом,η = τ / D. Динамическую вязкость (η) обычно выражают в пуазах (пз) или сантипуазах (1 спз = 0,01 пз). Жидкость имеет вязкость 1 пз, если напряжение сдвига 1 дин/см2 создает скорость сдвига 1 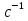 ).. В системе СИ динамическая вязкость выражается в паскаль-секундах (Па*с) или миллипаскаль-секундах (мПа*с). 1 сП = 1 мПа*с. ).. В системе СИ динамическая вязкость выражается в паскаль-секундах (Па*с) или миллипаскаль-секундах (мПа*с). 1 сП = 1 мПа*с.Кинематическую вязкость (ν), выраженную в метрах квадратных на секунду ( 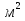 * *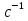 ).), получают делением величины динамической вязкости η на плотность жидкости ρ, выраженную в килограммах на метр кубический (кг× ).), получают делением величины динамической вязкости η на плотность жидкости ρ, выраженную в килограммах на метр кубический (кг×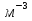 ), измеренную при той же температуре: ), измеренную при той же температуре:v = η / ρ. Кинематическую вязкость обычно выражают в стоксах (ст) или сантистоксах (1 сст = 0,01 ст), в системе СИ – в метрах квадратных на секунду ( 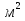 * *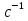 ) или миллиметрах квадратных на секунду ( ) или миллиметрах квадратных на секунду (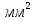 * *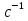 ). ).1 ст = 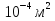 * *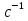 . .В ряде случаев требуется определить вязкость одной жидкости относительно другой – относительную вязкость ( 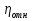 .). .).Часто вязкость выражают как удельную вязкость ( 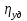 ), которая показывает, какая часть вязкости раствора обусловлена присутствием в нем растворенного вещества ), которая показывает, какая часть вязкости раствора обусловлена присутствием в нем растворенного веществаДля растворов полимеров вязкость является функцией молекулярных масс, формы, размеров и гибкости макромолекул. Чтобы определить структурные характеристики полимеров, приведенную вязкость экстраполируют к нулевой концентрации. В этом случае вводится понятие характеристической вязкости [η] |
