Технология как ограничение. Производственное множество и его свойства. Технологически и экономически эффективные способы производства
 Скачать 16.09 Mb.
|
Производственная функция – технологическая зависимость между затратами ресурсов и выпуском продукции. Если выражать формально, то производственная функция выглядит следующим образом: 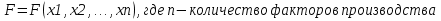 Допустим, что производственная функция описывает выпуск продукции в зависимости от затрат труда и капитала, то есть рассмотрим двухфакторную модель. Одно и то же количество продукции можно получить при различных сочетаниях затрат этих ресурсов. Можно использовать небольшое количество машин (т. е. обойтись небольшими затратами капитала), но при этом придется затратить большое количество труда; можно, напротив, механизировать те или иные операции, увеличить количество машин и за счет этого снизить затраты труда. Если при всех таких сочетаниях наибольший возможный объем выпуска остается постоянным, то эти сочетания изображаются точками, лежащими на одной и той же изокванте. То есть изокванта – это линия равного выпуска или количества. На графике x1 и x2 – это используемые ресурсы. 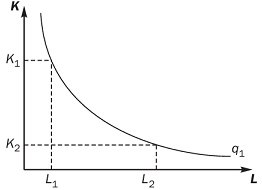 Зафиксировав другое количество произведенной продукции, получим другую извокванту , то есть у одной и той же производственной функции имеется карта изоквант. 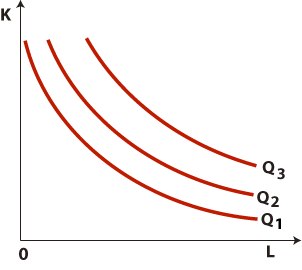 Свойства изоквант:
Для любого уровня выпуска возможно построить изокванту
Рассмотрим 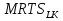 (замещение ТРУДОМ КАПИТАЛА). То есть, от какого количества капитала готов отказаться производитель, ради получения 1 единицы труда. Необходимо доказать, что данный показатель убывает. 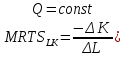 ) 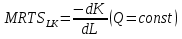 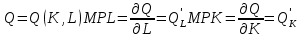 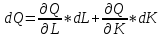Но так как Q=const, следовательно, dQ=0 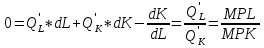 Как известно, предельный продукт труда убывает (так как рациональный производитель работает во второй стадии производства), следовательно, с увеличением труда MPL будет убывать, а MPK увеличиваться, так как количество капитала уменьшается, следовательно, 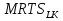будет убывать.Экономическая причина уменьшения MRTS состоит в том, что в большинстве отраслей факторы производства не являются полностью взаимозаменяемыми: они и дополняют друг друга в производственном процессе. Каждый фактор может делать то, что не может сделать или может сделать хуже другой фактор производства.
Эластичность замещения факторов производства — применяемый в экономической теории показатель, показывающий на сколько процентов необходимо изменить отношение факторов производства при изменении их предельной нормы замещения на 1 %, чтобы объём выпуска оставался неизменным. Определим предельную норму замещения капитала трудом при технологии 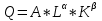 Тогда из предыдущего билета следует: 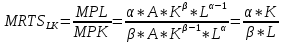 При графическом построении MRTS соответствует тангенсу угла наклона касательной к изокванте в точке, указывающей необходимые объемы труда и капитала для производства заданного объема продукции. При заданной технологии каждой величине капиталовооруженности труда (точке на изокванте) соответствует свое соотношение между предельными производительностями факторов производства. Иначе говоря, одной из специфических характеристик технологии является то, как сильно меняется соотношение предельных производительностей капитала и труда при небольшом изменении капиталовооруженности, то есть количества используемого капитала. Графически это отображается степенью кривизны изокванты. Количественной мерой этого свойства технологии является эластичностьзамещенияфакторовпроизводства, которая показывает, на сколько процентов должна измениться капиталовооруженность труда, чтобы при изменении соотношения производительностей факторов на 1% выпуск остался неизменным. Обозначим 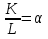 ; тогда эластичность замещения факторов производства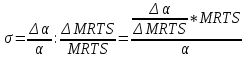 при Q=constВот это логарифмическое представление. Пздц) Обозначим  — предельную норму замещения -го фактора -ым фактором, а — отношение количества этих факторов, используемых в производстве. Тогда эластичность замещения будет равна: При этом можно показать, что Единственное, чего не смог найти – это вывод вот этой «…». Кривизна изокванты иллюстрирует эластичность замещения факторов при выпуске заданного объема продукта и отражает то, насколько легко один фактор может быть заменен другим. В том случае, когда изокванта похожа на прямой угол, вероятность замещения одного фактора другим крайне невелика. Если же изокванта имеет вид прямой линии с наклоном вниз, то вероятность замены одного фактора другим значительна. (подробнее смотри про разные виду функций в пятом билете) Более того, когда изокванта непрерывна, то она характеризует гибкость технологии. То есть у фирмы есть огромное количество вариантов производства. Для отменного понимания вот этого дерьма, ознакомься с 5ым, там все збс прописано.
Совершенная взаимозаменяемость ресурсов или линейная производственная функция Если ресурсы, используемые в процессе производства, являются абсолютно заменяемыми, то 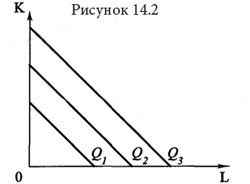 постоянна во всех точках изокванты, а карта изоквант имеет вид как на рисунке 14.2. (Примером такого производства может служить производство, допускающее как полную автоматизацию, так и ручное изготовление какого-либо продукта). Q=a*K+b*L, где K:L=b/a –пропорция замещения одного ресурса другим(b-точка пересецния Q1 оси ОК, a- оси OL) Постоянная отдача от масштаба, эластичность замещения ресурсов бесконечна, MRTSlk=-b/a, эластичность выпуска по труду – в, по капиталу – а. Фиксированная структура использования ресурсов, она же функция Леонова Если технологический процесс исключает замещение одного фактора на другой и требует использование обоих ресурсов в строго фиксированных пропорциях, производственная функция имеет вид латинской буквы , как на рисунке 14.3. 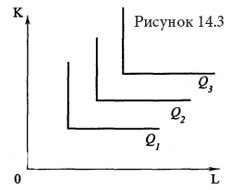 Примером подобного рода может служить работа землекопа (одна лопата и один человек). Увеличение одного из факторов без соответствующего изменения количества другого фактора нерационально, поэтому технически эффективными будут лишь угловые комбинации ресурсов (угловая точка — точка, где пересекаются соответствующие горизонтальная и вертикальная линии). Q=min(aK;bL);Постоянная отдача от масштаба, K:L=b:a пропорция дополнения, MRTSlk=0, эластичность замещения 0, эластичность выпуска 0. Функция Кобба-Дугласа 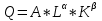A-характеризует технологию. 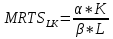 Эластичность замещения факторов может быть любой, отдача от масштаба 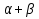 (1-постоянная, меньше единицы – убывающая, больше единицы возрастающая), эластичность выпуска по факторам производсвта для капитала – альфа, для труда –бета, эластичность замещения факторов 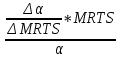 Функция CES Функция CES (CES — англ. Constant Elastisity of Substitution) — применяемая в экономической теории функция, обладающая свойством постоянной эластичности замещения. Иногда она используется также и для моделирования функции полезности. Данная функция применяется в первую очередь для моделирования производственной функции. Некоторые другие популярные производственные функции представляют собой частные или предельные случаи данной функции. 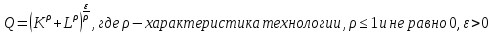 Отдача от масштаба зависит от 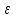 : больше 1, возрастающая отдача от масштаба, меньше 1 – убывающая отдача от масштаба, равно 1 – постоянная отдача от масштаба. 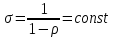 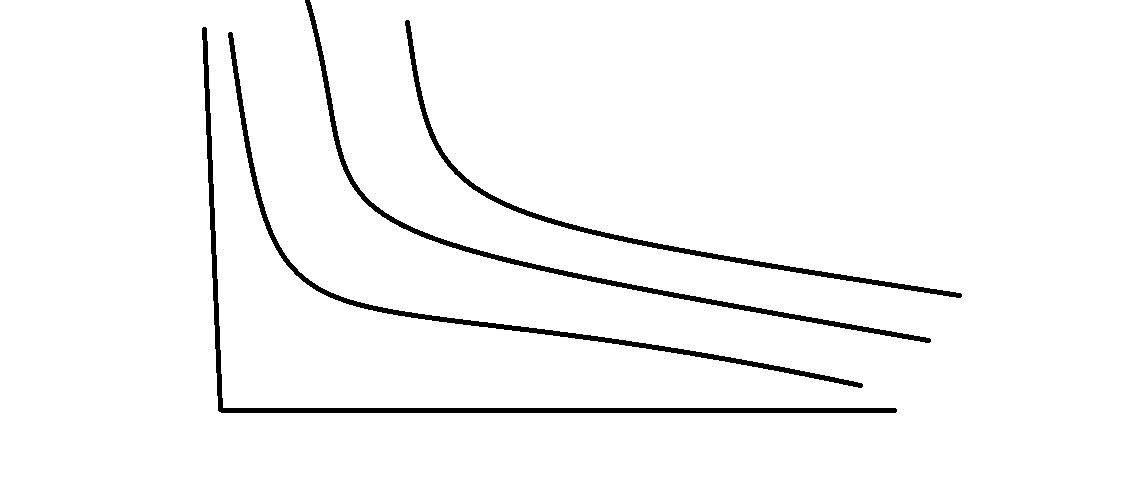 ДЛЯ ДАННЕОГО БИЛЕТА Я НЕ СМОГ НАЙТИ ЭЛАСТИЧНОСТЬ ВЫПУСКА ВООБЩЕ НИГДЕ НОРМАЛЬНУЮ
Экономические издержки - ценность других благ, которые можно было бы получить при наиболее выгодном использовании тех же ресурсов. В этом случае говорят об «альтернативных издержках». Альтернативные издержки возникают в мире ограниченных ресурсов, и поэтому все желания людей не могут быть удовлетворены. Если бы ресурсы были безграничны, то ни одно действие не осуществлялось бы за счет другого, т. е. альтернативные издержки любого действия были бы равны нулю. Очевидно, что в реальном мире ограниченных ресурсов альтернативные издержки положительны. Опираясь на понятие альтернативных издержек, можно сказать, что экономические издержки - это те выплаты, которые фирма обязана сделать, или те доходы, которые фирма обязана обеспечить поставщику ресурсов для того, чтобы отвлечь эти ресурсы от использования в альтернативных производствах. Эти выплаты могут быть либо внешними, либо внутренними. Внешние издержки представляют собой плату за ресурсы (сырье, топливо, транспортные услуги – все то, что фирма не производит сама для создания какого-либо товара) поставщикам, не принадлежащим к числу владельцев данной фирмы. Кроме того, фирма может использовать определенные ресурсы, принадлежащие ей самой. Издержки на собственный и самостоятельно используемый ресурс представляют собой неоплачиваемые, или внутренние, издержки. С точки зрения фирмы эти внутренние издержки равны денежным платежам, которые могли бы быть получены за самостоятельно используемый ресурс при наилучшем - из возможных способов - его применении.Внутренние издержки включают также нормальнуюприбыль как минимальное вознаграждение предпринимателя, необходимое для того, чтобы он продолжал свое дело и не переключился на другое. Таким образом, экономические издержки выглядят так: Экономические издержки = Внешние издержки + Внутренние издержки (включая нормальную прибыль) Изокоста– прямая, показывающая все комбинации факторов производства при фиксированном объеме общих затрат. Набор изоквант отдельной фирмы (карта изоквант) показывают технически возможные комбинации ресурсов, обеспечивающие фирме соответствующие объемы выпуска. При выборе оптимальной комбинации ресурсов производитель должен учитывать не только доступную ему технологию, но и свои финансовые ресурсы, а также цены на соответствующие факторы производства. Совокупность этих двух факторов определяет область доступных производителю экономических ресурсов (его бюджетное ограничение). Бюджетное ограничение производителя может быть записано в виде неравенства: PK*K+PL*L 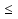 TC, гдеPK,PL-цена капитала, цена труда; TC – совокупные издержки фирмы на приобретение ресурсов. Если производитель (фирма) полностью расходует свои средства на приобретение данных ресурсов, получаем следующее равенство: PK*K+PL*L=TC На графике изокоста определяется в осях L,K, поэтому для построения, удобно привести равенство в следующий вид: 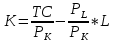 –уравнение изокосты.Наклон линии изокосты определяется отношением рыночных цен на труд и на капитал: ( - PL/PK) K L |
