Технология как ограничение. Производственное множество и его свойства. Технологически и экономически эффективные способы производства
 Скачать 16.09 Mb. Скачать 16.09 Mb.
|
|
Функции чистого (избыточного) спроса. Закон Вальраса. Спрос на какой-то товар является функцией цен всех других товаров, дохода и количества потребителей. Возьмем для примера два товара: X, Y. Две фирмы: А, В. Функции чистых (избыточных) спросов на эти товары: Для фирмы А: 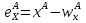 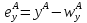 Добавим зависимость от цен:  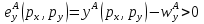 Для фирмы В: 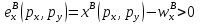 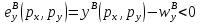 Понятие и функция избыточного спроса позволяют рассматривать предложение как отрицательный избыток спроса, а спрос – как положительный его избыток. В этой модели различие между предложением и спросом исчезает. Общий избыточный спрос (отдельно по товарам):  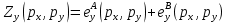 Условием общего равновесие является равенство нулю всех общих избыточных спросов по всем товарам.   Рх*,Ру*-равновесные цены 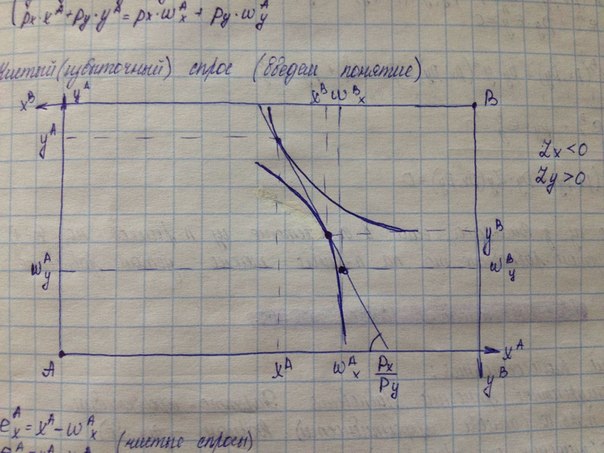 Закон Вальраса: стоимость всех общих избыточных спросов равна 0. Доказательство:  Следствие из закона Вальраса: если в экономической системе из n-рынков на (n-1) рынке устанавливается равновесие, то на n-рынке также устанавливается равновесие.
28.8. Существование равновесия В приведенном выше примере имелись конкретные уравнения для функции спроса каждого потребителя, и, решив их, мы могли найти их точное значение равновесной цены. Однако вообще говоря, мы не располагали точными алгебраическими формулами, выражающими спрос каждого потребителя. Вполне можно было задать следующий вопрос: откуда известно, что существует какая-то совокупность цен, при которой на каждом рынке спрос равен предложению? Этот вопрос называют вопросом о существовании конкурентногоравновесия. Существование конкурентного равновесия важно в том плане, что оно служит "проверкой на состоятельность" для различных моделей, рассмотренных нами в предшествующих главах. Какой смысл строить сложные теории механизма установления конкурентного равновесия, если такое равновесие обычно никогда не существует? Экономисты раннего периода отмечали, что на рынке с k товарами должно определяться k — 1 относительных цен и что имеется k — 1 описывающих равновесие уравнений, в которых утверждается, что на каждом из рынков спрос должен равняться предложению. Они заявляли, что поскольку число уравнений равняется числу неизвестных, должно существовать решение, которое удовлетворяет всем уравнениям. Вскоре экономисты обнаружили ошибочность подобной аргументации. Чтобы доказать, что равновесное решение должно существовать простого подсчета числа уравнений и числа неизвестных недостаточно. Имеются, однако, математические инструменты, которые могут быть использованы для установления факта существования конкурентного равновесия. Решающей оказывается при этом предпосылка о непрерывности функции совокупного избыточного спроса. Грубо говоря, это означает, что малые изменения цен должны приводить лишь к малым изменениям совокупного спроса: малое изменение цен не должно иметь своим результатом большой скачок в количестве спроса. При каких условиях функции совокупного спроса будут непрерывными? По существу имеются два рода условий, гарантирующих эту непрерывность. Одно из них состоит в том, что должна быть непрерывной функция спроса каждого индивида — так что малые изменения цен будут приводить лишь к малым изменениям спроса. Оказывается, для этого требуется, чтобы предпочтения каждого потребителя были выпуклыми, о чем шла речь в гл.3. Другое условие является более общим. Даже если функции спроса отдельных потребителей прерывны до тех пор пока все потребители мелки по сравнению с размерами рынка, функция совокупного спроса будет непрерывной. Это последнее условие выглядит вполне разумным. В конце концов, предпосылка о конкурентном поведении имеет смысл только тогда, когда существует множество потребителей, мелких по отношению к размерам рынка. Это как раз то самое условие, соблюдение которого требуется для того, чтобы функции совокупного спроса были непрерывными. А непрерывность — не что иное, как гарантия существования конкурентного равновесия. Таким образом, те самые предпосылки, которые делают постулируемое поведение разумным, гарантируют наличие у теории равновесия самостоятельного содержания. 28.9. Равновесие и эффективность Мы проанализировали рыночный обмен в рамках модели чистого обмена. При этом мы получили конкретную модель обмена, которую можно сравнить с общей моделью обмена, обсуждавшейся в начале настоящей главы. При рассуждениях о применимости модели конкурентного рынка может возникнуть вопрос о том, способен ли этот механизм действительно исчерпать все выгоды от обмена. Не останется ли еще каких-то сделок, которые люди захотят осуществить, после того, как в результате процесса обмена мы попали в положение конкурентного равновесия, в котором спрос равен предложению на каждом из рынков? Этот вопрос не что иное, как вопрос о том, является ли рыночное равновесие эффективным по Парето: захотят ли рыночные индивиды совершить еще какие-то обменные сделки после совершения обмена по конкурентным ценам? Ответ виден при внимательном рассмотрении рис.28.4: распределение, соответствующее рыночному равновесию, оказывается эффективным по Парето. Доказательство этого: распределение в ящике Эджуорта является эффективным по Парето, если множество наборов, предпочитаемых индивидом A, не пересекает множества наборов, предпочитаемых индивидом B. Однако при рыночном равновесии множество наборов, предпочитаемых индивидом A, должно лежать над его бюджетным множеством, и то же самое справедливо для B, при том, что "над" означает "над, с точки зрения B". Следовательно, два множества предпочитаемых распределений не могут пересечься. Это означает, что не существует распределений, которые оба индивида предпочли бы равновесному распределению, поэтому равновесное распределение эффективно по Парето. 28.10. Алгебра эффективности Мы можем показать это и алгебраически. Предположим, что рыночное равновесие не является эффективным по Парето. Покажем, что данное предположение ведет к логическому противоречию. Утверждение, что рыночное равновесие не является эффективным по Парето, означает, что существует какое-то другое практически осуществимое распределение ( 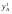 , , 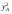 , , 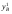 , , 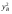 ), такое, что ), такое, что 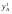 + + 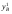 = = 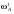 + + 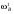 (28.1) (28.1)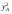 + + 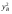 = = 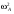 + + 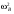 (28.2) (28.2)и ( 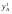 , ,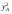 ) A( ) A( , ,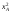 ) (28.3) ) (28.3)( 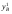 , ,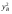 ) B( ) B(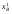 , ,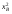 ). (28.4) ). (28.4)Два первых уравнения означают, что распределение y практически осуществимо, а два следующих — что каждый из индивидов предпочитает его распределению x. (Символы A и B относятся к предпочтениям индивидов A и B.) Однако согласно гипотезе мы имеем рыночное равновесие, в котором каждый из индивидов приобретает лучший набор из числа доступных. Если ( 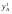 , ,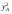 ) лучше набора, выбираемого A, значит, он должен стоить дороже, чем A может себе позволить; аналогичным образом можно рассуждать и для B: ) лучше набора, выбираемого A, значит, он должен стоить дороже, чем A может себе позволить; аналогичным образом можно рассуждать и для B:p1 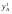 + p2 + p2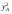 >p1 >p1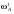 + p2 + p2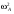 , ,p1 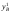 + p2 + p2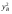 >p1 >p1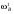 + p2 + p2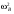 . .Теперь сложим два этих неравенства, получив при этом p1( 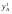 + +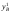 ) + p2( ) + p2(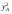 + +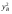 ) >p1( ) >p1(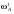 + +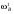 ) + p2( ) + p2(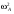 + +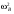 ). ).Выполнив соответствующие подстановки из уравнений (28.1) и (28.2), получим p1( 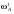 + +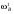 ) + p2( ) + p2(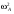 + +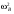 ) >p1( ) >p1(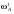 + +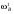 ) + p2( ) + p2(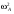 + +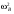 ), ),что, очевидно, является противоречием, поскольку левая и правая части выражения одинаковы. Мы вывели это противоречие, приняв в качестве предпосылки, что рыночное равновесие неэффективно по Парето. Следовательно, указанная предпосылка должна быть неверной. Отсюда следует, что все рыночные равновесия эффективны по Парето: этот результат известен как первая теорема экономики благосостояния. Первая теорема экономики благосостояния гарантирует, что конкурентный рынок исчерпывает все выгоды от обмена: равновесное распределение, достигнутое совокупностью конкурентных рынков, с необходимостью будет эффективным по Парето. У такого распределения могут отсутствовать какие-либо другие желаемые свойства, но оно обязательно будет эффективным. В частности, первая теорема экономики благосостояния ничего не говорит о распределении экономических выгод. Рыночное равновесие может не давать "справедливого" распределения — если индивид A владел всем в самом начале, он будет всем владеть и после обмена. Это будет эффективно, но, возможно, не очень справедливо. Однако, в конце концов, эффективность тоже чего-то стоит, и приятно сознавать, что с помощью столь простого рыночного механизм, как тот, который был нами описан, можно достичь эффективного распределения. ПРИМЕР: Монополия в ящике Эджуорта Чтобы лучше понять первую теорему экономики благосостояния, полезно рассмотреть другой механизм распределения ресурсов, который не ведет к эффективным исходам. Хороший пример такого рода дает нам поведение потребителя как монополиста. Допустим, что аукционщика больше нет и что индивид A намеревается назначать цену индивиду B, а индивид B будет решать, какое количество товаров он хочет обменять по назначенным ценам. Предположим далее, что A известна кривая спроса B и что он попытается выбрать такую совокупность цен, которая максимально повысит его благосостояние при данном поведении B в отношении спроса. Чтобы исследовать равновесие, возникающее в результате этого процесса, надо вспомнить определение кривой "цена-потребление" потребителя. Кривая "цена-потребление", о которой шла речь в гл.6, представляет все точки оптимального выбора потребителя при различных ценах. Кривая "цена-потребление" индивида B представляет те наборы, которые он купит при различных ценах, — иными словами, она описывает поведение B в отношении спроса. Если мы нарисуем бюджетную линию для B, то точка пересечения этой бюджетной линией его кривой "цена-потребление" будет точкой оптимального потребления B. Следовательно, если индивид A хочет предложить индивиду B цены, при которых благосостояние A было бы возможно более высоким, ему следует найти ту точку кривой "цена-потребление" индивида B, в которой полезность для A — наивысшая. Такой выбор показан на рис.28.5. Этот оптимальный выбор, как обычно, характеризуется условием касания: кривая безразличия индивида A касается кривой "цена-потребление" индивида B. Если бы кривая "цена-потребление" индивида B пересекала кривую безразличия индивида A, существовала бы некая точка кривой "цена-потребление" индивида B, которую индивид A предпочитал бы другим — поэтому мы не могли бы находиться в точке, оптимальной для A. Определив местонахождение этой точки (обозначенной на рис.28.5 буквой X), мы просто проводим бюджетную линию из точки начального запаса до данной точки. При ценах, порождающих данную бюджетную линию, B предпочтет набор X, и благосостояние A будет наиболее высоким из возможных. Является ли это распределение эффективным по Парето? Вообще, следует ответить "нет". Чтобы это увидеть, просто обратите внимание на то, что в точке X кривая безразличия индивида A не будет касаться бюджетной линии и поэтому кривая безразличия индивида A не будет касаться кривой безразличия индивида B. Кривая безразличия индивида A касается кривой "цена-потребление" индивида B, но не может касаться его кривой безразличия. Монопольное распределение неэффективно по Парето. Фактически оно неэффективно по Парето в точности в том же смысле, в каком неэффективность монополии была описана в гл.23. В пределе индивид A хотел бы продать больше по равновесным ценам, но он может сделать это, только снизив цену, по которой продает товар, а это снизит его доход, получаемый от всех допредельных продаж. Как мы видели в гл.23, монополист, проводящий совершенную ценовую дискриминацию, в конечном счете будет производить эффективный объем выпуска. Вспомним, что монополист, проводящий ценовую дискриминацию, — это такой монополист, который способен продать каждую единицу товара индивиду, готовому заплатить за эту единицу больше всех. Как выглядит поведение монополиста, осуществляющего совершенную ценовую дискриминацию, в ящике Эджуорта? 
Ответ дает рис.28.6. Начнем движение в точке начального запаса W и представим, что A продает B каждую единицу товара 1 по другой цене —цене, при которой B совершенно безразлично, покупать эту единицу товара или не покупать. Следовательно, после того, как A продаст ему первую единицу, B останется на той же самой кривой безразличия, проходящей через W. Затем A продает B вторую единицу товара 1 по максимальной цене, которую тот готов заплатить. Это означает, что распределение смещается далее влево, но остается на кривой безразличия индивида B, проходящей через W. Индивид A продолжает продавать B единицы товара таким же образом, сдвигаясь тем самым, вверх по кривой безразличия индивида B в поисках самой оптимальной для себя, индивида A, точки, обозначенной на рис.28.6 X. 
Как нетрудно увидеть, такая точка должна быть эффективной по Парето. Благосостояние индивида A будет в ней максимально возможным при данной кривой безразличия индивида B. В такой точке индивид A сумел извлечь весь излишек потребителя индивида B: благосостояние B не выше, чем в точке его начального запаса. Два этих примера служат полезными ориентирами при размышлениях о первой теореме экономики благосостояния. Обычный монополист дает нам пример механизма распределения ресурсов, приводящего к неэффективному равновесию, а монополист, осуществляющий ценовую дискриминацию, — пример другого механизма, приводящего к эффективному равновесию. |
