Технология как ограничение. Производственное множество и его свойства. Технологически и экономически эффективные способы производства
 Скачать 16.09 Mb.
|
|
Минимизация издержек при заданном уровне выпуска. Использование метода Лагранжа для решения задачи минимизации издержек. Условия оптимальности первого и второго порядков. Экономический смысл множителя Лагранжа в задаче минимизации.  В долгосрочном периоде все факторы являются переменными. Графически задача состоит в том, чтобы найти на изокванте, отражающей фиксированный выпуск, точку, с которой связана самая низкая изокоста. y-фиксированный объем выпускаемой продукции в LR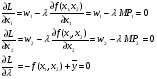 Функция Лагранжа:Преобразовав первые два уравнения, получим: MRTS – предельная норма технологического замещения  ,MP – предельный продукт (1) или (2) w1,w2– цены 1 и 2 ресурсов Последнее уравнение отражает равенство наклонов изокванты и изокосты. X2 Изокосты TC=w1x1+w2x2 X2* Изокванта f(x1,x2)=y(с черточкой сверху) X1* X1 Экономический смысл множителя Лагранжа (лямбдочка):  Решением задачи Лагранжа будут оптимальные значения количества факторов, которые обеспечивают минимальные затраты при заданном выпуске: 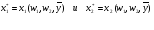 Условием первого порядка является нахождение оптимального значения количества факторов, которые обеспечивают минимальные затраты при данном выпуске. Условием второго порядка является матрица Гессена, доказывающая единственность решения. 
Выбор количеств факторов, минимизирующих издержки фирмы, вообще говоря, зависит от цен факторов и от того объема выпуска, который фирма хочет производить, поэтому мы записываем эти выбранные количества факторов в виде x1(w1, w2, y) и x2(w1, w2, y). Это так называемые функции условного спроса на факторы, или функциипроизводного спроса на факторы. Они показывают взаимосвязь между ценами и выпуском и оптимальный выбор фирмой количества факторов при условии производства фирмой заданного объема выпуска y. Обратите особое внимание на различие между функциями условного спроса на факторы и функциями спроса на факторы, максимизирующего прибыль, которые были рассмотрены в предыдущей главе. Функции условного спроса на факторы показывают выбор, минимизирующий издержки при заданном объеме выпуска; функции же спроса на факторы, максимизирующего прибыль, показывают выбор, максимизирующий прибыль при заданной цене фактора. Функции условного спроса на факторы, как правило, не являются непосредственно наблюдаемыми: они представляют собой гипотетическое построение и отвечают на вопрос, сколько каждого фактора использовала бы фирма, если бы хотела произвести заданный объем выпуска самым дешевым способом. Однако функции условного спроса на факторы полезны в качестве способа отделения задачи определения оптимального объема выпуска от задачи определения метода производства, минимизирующего издержки. На первом курсе были рассмотрены понятия альтернативных,бухгалтерских и экономических издержек [повторить!].Мы везде далее,как это принято в экономическойтеории под издержками будем понимать экономические издержки, предполагая в наших моделях под L – однородные трудовые ресурсы, под K – однородный капитал, и будем считать, что фирмы покупают L и K на совершенно конкурентных рынках по преобладающим ставкам зарплаты или арендной платы w и r. Это предположение говорит о том, что w и r от фирмы никак не зависят, т.е. являются параметрами. Будем также считать, что исходя из каких-либо соображений, фирма определила для себя желаемый объем выпуска Q* . Общие издержки фирмы в течение некоторого периода: TC=wL+rK, выпуск Q=f (K, L). Перед фирмой стоит задача произвести заданный объем выпуска Q* при минимальных издержках производства, т.е.: 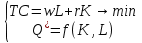 Решая ее методом Лагранжа получим: 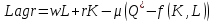  => => Получили уравнение  , что получали на первом курсе, анализируя графическую модель выбора производителя оптимального набора ресурсов:TC =wL+ rK Q*= f (K , L) Здесь ограничением служит фиксированный объем выпуска Q* - фиксированная изокванта; графиком издержек является отрезок прямой – изокоста с наклоном –w/r Решив задачу минимизации издержек, мы получим функции условного или производного спроса на ресурсы: K *= K *(w, r, Q), L*= L*(w, r, Q). Условного,т.к.они показывают связь между ценами,выпуском и количествомиспользуемых ресурсов при условии производства фирмой заданного непосредственно наблюдаемыми, они дают ответ на вопрос: «сколько каждого фактора использовала бы фирма, если бы хотела произвести заданный объем выпуска наиболее дешевым способом». Условие второго порядка мы не проверяем здесь по тем же причинам, что и в теории потребителя – свойства изоквант (т.е. производственной функции) таковы, что найденная критическая точка будет точкой минимума (выпуклость изоквант или убывание MRTS).
В гл. 17 мы обсуждали идею отдачи от масштаба применительно к производственной функции. Вспомним, что технология характеризуется возрастающей, убывающей или постоянной отдачей от масштаба в зависимости от того, является ли f(x1, x2) величиной большей, меньшей или равной tf(x1, x2) для всех t >1. Оказывается, существует отчетливо прослеживаемая взаимосвязь между типом отдачи от масштаба, характеризующим производственную функцию, и поведением функции издержек. Предположим вначале, что мы имеем дело с естественным случаем постоянной отдачи от масштаба. Представьте, что мы решили задачу минимизации издержек для производства одной единицы выпуска, поэтому нам известна функция единичных издержекc(w1, w2, 1). Какой же самый дешевый способ произвести y единиц выпуска? Ответ прост: мы используем каждого фактора просто в y раз больше, чем для производства одной единицы выпуска. Это означает, что минимальные издержки производства y единиц выпуска составят просто c(w1, w2, 1)y. В случае постоянной отдачи от масштаба функция издержек является линейной по выпуску. Что если мы имеем дело с возрастающей отдачей от масштаба? В этом случае оказывается, что с возрастанием выпуска издержки возрастают медленнее, чем при линейной зависимости. Если фирма решает произвести выпуск в два раза больше, она может сделать это при менее чем удвоенных издержках, при условии, что цены факторов остаются постоянными. Это естественное следствие идеи возрастающей отдачи от масштаба: если фирма удваивает используемое количество факторов, то она более чем удвоит выпуск. Следовательно, если она хочет произвести выпуск вдвое больше, она сможет сделать это, используя менее чем в два раза больше каждого фактора. Однако удвоение используемого количества каждого фактора увеличит издержки ровно в два раза. Поэтому увеличение используемого количества каждого фактора менее чем вдвое приведет к возрастанию издержек менее чем в два раза: это говорит нам о том, что функция издержек с ростом выпуска будет возрастать медленнее, чем при линейной зависимости. Аналогичным образом, если технология характеризуется убывающей отдачей от масштаба, функция издержек с ростом выпуска будет возрастать быстрее, чем при линейной зависимости. С удвоением выпуска издержки более чем удвоятся. Эти факты могут быть выражены с позиций поведения функции средних издержек. Функция средних издержек — это просто издержки на единицу производства y единиц выпуска: AC(y) = 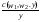 .Если технология характеризуется постоянной отдачей от масштаба, то, как мы видели выше, функция издержек имеет вид c(w1, w2, y) = c(w1, w2, 1)y . Это означает, что функция средних издержек будет иметь вид AC(w1, w2, y) = 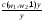 = c(w1, w2, 1).Иными словами, издержки на единицу выпуска будут постоянными, независимо от того, какой объем выпуска захочет производить фирма. Если технология характеризуется возрастающей отдачей от масштаба, то издержки с ростом выпуска растут медленнее, чем при линейной зависимости, так что средние издержки демонстрируют убывающую зависимость от выпуска: с возрастанием выпуска средние издержки производства имеют тенденцию к снижению. Аналогичным образом, если технология характеризуется убывающей отдачей от масштаба, средние издержки с ростом выпуска будут возрастать. Как мы видели ранее, данная технология может иметь области возрастающей, постоянной или убывающей отдачи от масштаба — выпуск при различных объемах производства может расти быстрее с той же скоростью или медленнее, чем масштабы действий фирмы. Подобным же образом при различных объемах производства функция издержек может убывать, оставаться постоянной или возрастать. В следующей главе мы исследуем эти возможности более подробно. С настоящего же момента нас больше всего будет интересовать поведение функции издержек относительно переменной выпуска. Мы будем представлять цены факторов большей частью фиксированными на некоторых предопределенных уровнях и считать издержки зависящими только от выбора фирмой объема выпуска. Таким образом, во всех остальных главах книги мы будем записывать функцию издержек как функцию одного только выпуска: c(y). ПОДРОБНЕЕ: ВЭРИАН гл.19
(*Линия оптимального роста, путь развития, траектория расширения производства,…). Показывает, как изменяются количество используемых ресурсов при увеличении объема выпуска (при неизменных ценах на ресурсы) и min издержек. Она не всегда является прямой, изменение использованных ресурсов может происходить по-разному. Форма линии роста зависит от формы изоквант (т.е. от свойств производственной функции). Линия роста будет представлять собой луч, исходящий из начала координат, если производственная функция является однородной первой степени, т.е. расширение производства происходит с постоянной отдачей от масштаба. Линия роста – совокупность точек, в которых фирма минимизирует издержки. Линия роста не всегда имеет положительный наклон. Возможны технологии производства, когда увеличение выпуска можно получить при уменьшении использования какого-либо ресурса, например, труда. В данной ситуации L является инфериорным фактором производства. Тогда нормальные ресурсы – те, при увеличении использования которых происходит увеличение выпуска Доказательство того, что уравнение линии роста  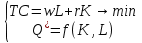Решая ее методом Лагранжа получим: 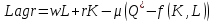=>=>Изменение цен на факторы производства, эффект выпуска. ГАЛЬПЕРИН, глава 7.6 http://seinst.ru/files/galper_7_6.pdf Там же можно прочитать еще про линию роста.
Различают издержки в длительном периоде или д о л г о с р о ч н ы е и з д е р ж к и CL (LongCosts) и издержки в коротком периоде, или к р а т к о с р о ч н ы е и з д е р ж к и CS (ShortCosts). В длительном периоде все ресурсы являются переменными. В коротком периоде часть ресурсов являются постоянными, и их количество не может быть изменено в пределах данного периода. Для краткосрочного периода издержки можно разделить на два вида: Классификация издержек 26п е р е м е н н ы е и з д е р ж к и СV (VariedCosts), изменяющиеся при изменении объёма выпуска, и п о с т о я н н ы е и з д е р ж к и СF (FixedCosts), не зависящие от объёма производства. К переменным издержкам относятся затраты на сырьё, материалы, оплату труда производственных работников; к постоянным - затраты на содержание зданий, сооружений, оборудования, административно-управленческие расходы, арендная плата, налоги и т.п. Таким образом, издержки в коротком периоде могут быть представлены как сумма постоянных и переменных издержек 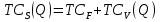 (2.1)где CS(Q) – краткосрочные издержки на выпуск Q единиц продукции; СF - постоянные издержки за период; СV (Q) – переменные издержки на производство Q единиц продукции. Для анализа издержек широко применяют такие показатели, как предельные и средние (удельные) издержки. П р е д е л ь н ы е и з д е р ж к и MC характеризуют изменение затрат, обусловленное изменением выпуска продукции на единицу, и определяются как: 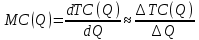 ,где символом “∆ ” обозначено конечное изменение показателя. Этот показатель применим для анализа затрат и в долгосрочном, и в краткосрочном периодах. Поскольку постоянные издержки не зависят от объема выпуска, то краткосрочные предельные издержки, то можно представить так: 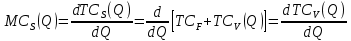 Отсюда ясно, что краткосрочные предельные затраты характеризуют прирост переменных затрат при единичном приращении объема выпуска. С р е д н и е и з д е р ж к и AC (Average Costs) характеризуют затраты, приходящиеся на единицу продукции: 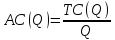 Учитывая (2.1), краткосрочные средние издержки можно представить следующим образом: 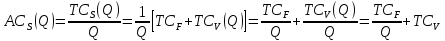 где cV - удельные переменные издержки (переменные издержки, приходящиеся на единицу продукции). Отсюда следует, что краткосрочные средние издержки снижаются с увеличением объема продукции, то есть имеет место э к о н о м и я н а р а с ш и р е н и и п р о и з в о д с т в а в к р а т к о с р о ч н о м п е р и о д е . http://freakonomics.ru/text/Glava20 http://freakonomics.ru/text/Glava19 ПОДРОБНО ТУТ!
Функцию краткосрочных издержек определяют как минимальные издержки производства данного объема выпуска при изменении количеств лишь переменных факторов производства.предположим, что в коротком периоде количество фактора 2 фиксировано на каком-то предопределенном уровне  , но в длительном периоде оно может изменяться. Тогда функция краткосрочных издержек определяется задачейcs(y, ) = minw1x1 + w2x1 при f(x1, 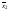 ) = y.Обратите внимание, что в общем случае минимальные издержки производства y единиц выпуска в коротком периоде будут зависеть от количества и стоимости имеющегося постоянного фактора. В случае двух факторов производства эту задачу минимизации решить нетрудно: мы просто находим наименьшее количество x1, такое, что f(x1, ) = y. Однако если имеется много факторов производства, являющихся в коротком периоде переменными, решение задачи минимизации издержек потребует более сложных расчетов.Функция краткосрочного спроса на фактор 1 есть то количество фактора 1, которое минимизирует издержки. В общем случае это количество зависит от цен факторов, а также от количеств постоянных факторов, так что мы записываем функции краткосрочного спроса на факторы как x1 = 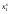 (w1, w2, , y),x2 = .Из этих уравнений следует, например, что если в коротком периоде площади производственного здания постоянны, то число рабочих, которое хочет нанять фирма при любом заданном наборе цен и выбранном объеме выпуска, будет, как правило, зависеть от площадей здания. Обратите внимание, что согласно определению функции краткосрочных издержек cs(y, ) = w1 (w1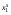, w2, , y) + w2.Это выражение подтверждает, что минимальные издержки производства выпуска y есть издержки, связываемые с использованием комбинации факторов производства, минимизирующей издержки. Это верно по определению, но тем не менее оказывается полезным. Функция долгосрочных издержек в этом примере определяется задачей cs(y) = min w1x1 + w2x2 x1, x2 при f(x1, x2) = y. Здесь могут изменяться оба фактора. Долгосрочные издержки зависят, кроме цен факторов, только от объема выпуска, который хочет производить фирма. Запишем функцию долгосрочных издержек как c(y), а функции долгосрочного спроса на факторы — как x1 = x1(w1, w2, y), x2 = x2(w1, w2, y). Мы также можем записать функцию долгосрочных издержек как c(y) = w1x1(w1, w2, y) + w2x2(w1, w2, y). Как и раньше, это выражение свидетельствует, что минимальные издержки есть издержки, которые фирма несет при условии использования комбинации факторов, минимизирующей издержки. Между функциями краткосрочных и долгосрочных издержек существует интересная взаимосвязь, которая будет использована нами в следующей главе. Для простоты предположим, что цены факторов фиксированы на неких предопределенных уровнях, и запишем функции долгосрочного спроса на факторы в виде x1 = x1(y) x2 = x2(y). Тогда функцию долгосрочных издержек можно записать также в виде c(y) = cs(y, x2(y)). Чтобы убедиться в правильности записи, подумайте о том, что она означает: в данном уравнении говорится, что минимальные издержки для случая, когда все факторы являются переменными, есть не что иное как минимальные издержки для случая, когда количество фактора 2 фиксировано на уровне, минимизирующем долгосрочные издержки. Следовательно, долгосрочный спрос на переменный фактор — выбор, минимизирующий издержки, — задан уравнением x1(w1, w2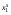, y) = (w1, w2, x2(y), y)В этом уравнении утверждается, что в длительном периоде количество переменного фактора, минимизирующее издержки, есть то количество фактора, которое фирма выбрала бы в коротком периоде, если бы оказалось, что в этом периоде у нее имелось количество постоянного фактора, минимизирующее издержки в длительном периоде. |