Технология как ограничение. Производственное множество и его свойства. Технологически и экономически эффективные способы производства
 Скачать 16.09 Mb. Скачать 16.09 Mb.
|
|
Постоянные и квазипостоянные издержки В гл. 18 мы провели различие между постоянными и квазипостоянными факторами. Постоянные факторы — это факторы, которые должны оплачиваться независимо от того, производится какой-либо выпуск или нет. Квазипостоянные факторы должны оплачиваться только в случае, если фирма решает производить положительный объем выпуска. Естественно было бы подобным же образом определить постоянные и квазипостоянные издержки. Постоянные издержки — это издержки, связываемые с постоянными факторами: они не зависят от объема выпуска и, в частности, должны оплачиваться независимо от того, производит фирма какой-то выпуск или нет. Квазипостоянные издержки — это издержки, которые тоже не зависят от объема выпуска, но должны оплачиваться только при условии производства фирмой положительного объема выпуска. В длительном периоде по определению постоянных издержек не бывает, однако вполне могут существовать квазипостоянные издержки. Если началу производства какого-то объема выпуска должна предшествовать затрата какой-то постоянной суммы, то можно говорить о наличии квазипостоянных издержек.
При найме дополнительного работника у фирмы увеличиваются переменные затраты и одновременно объем продукции. Следовательно, произойдет некоторое изменение средних и предельных издержек фирмы. Логично предположить, что это изменение будет зависеть от производительности нанимаемого работника. Рассмотрим указанную зависимость при условии, что труд является единственным переменным ресурсом, и ставка заработной платы не меняется при изменении объема нанимаемого труда: 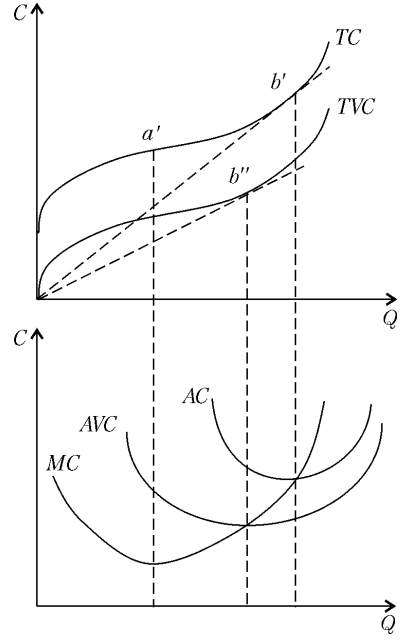 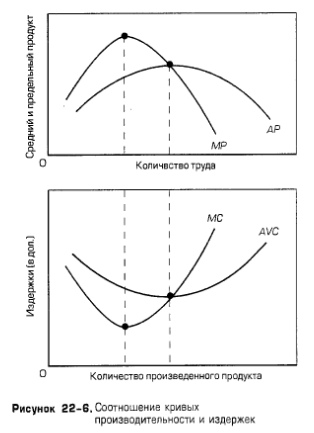 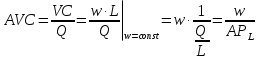 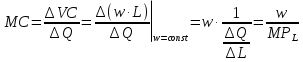 Далее рассмотрим издержки в краткосрочном периоде, где капитал – постоянный ресурс, издержки на который не зависят от объема выпуска (FC), и труд – переменный ресурс, издержки на который зависят от выпуска (VC). Общие совокупные издержки, таким образом, TC=FC+VC. На графике FC будет выглядеть как горизонтальная прямая исходящая из той же точки, что и TC. Функция AFC, в свою очередь, выглядит как гипербола.
Каждая фирма в тот или иной момент имеет определенные масштабы производства (объем выпуска продукции), которым соответствует та или иная кривая издержек краткосрочного периода. Таких кривых существует столько, сколько масштабов производства исследуется. Меняя эти масштабы, фирма переходит от одной кривой средних издержек краткосрочного периода к другой. При этом средние издержки до определенного объема выпуска будут уменьшаться (при переходе от АС1 к АС3), а затем начнут постепенно возрастать (при переходе от АС3 к АС5) (см. рис). 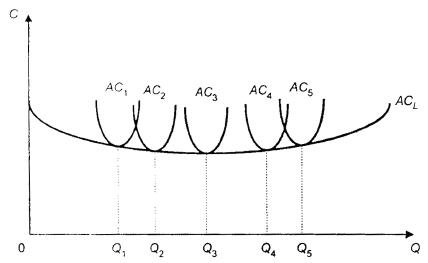 В проведенных выше рассуждениях предполагалось, что можно выбирать непрерывное количество фиксированного фактора производства. Таким образом, каждому объему выпуска соответствует единственный оптимальный размер этого ресурса. Однако можно посмотреть также, что произойдет, если выбор ограничен лишь несколькими разными размерами ресурса с постоянными издержками. Допустим, например, что имеются четыре различных варианта выбора размера завода, k1, k2, k3 и k4. На рис. изображены четыре различные кривые средних издержек, соответствующих этим размерам завода. На графике наглядно видно, что и в этом случае, кривая долгосрочных средних издержек есть нижняя огибающая кривых краткосрочных средних издержек. Что из этого следует применительно к предельным издержкам? Рассмотрим случай с дискретными размерами завода. В этой ситуации кривая долгосрочных предельных издержек состоит, как показано на 3. рис., из соответствующих кусков кривых краткосрочных предельных издержек. При каждом объеме выпуска мы смотрим, в соответствии с какой кривой краткосрочных средних издержек мы производим, а затем на то, какие предельные издержки связываются с данной кривой. 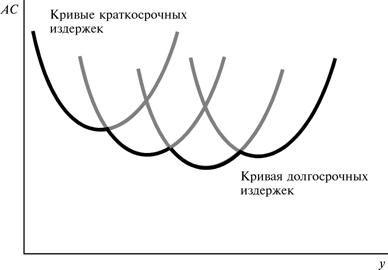 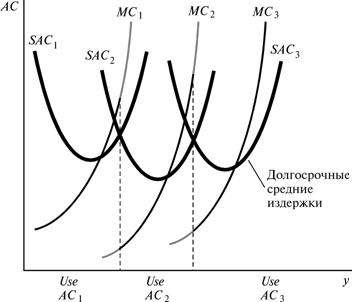 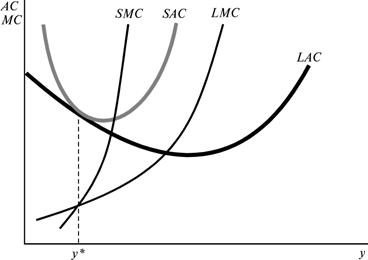 Это должно быть верно независимо от того, сколько у нас имеется различных размеров завода, так что в случае их непрерывного количества получаем картину, подобную изображенной на рис.4. Долгосрочные предельные издержки при любом объеме выпуска y должны равняться краткосрочным предельным издержкам, связанным с размером завода, оптимальным для производства выпуска y.
Предположим, что у вас имеются два завода с двумя различными функциями издержек 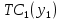 и и  . Задача: произвести Q единиц выпуска самым дешевым способом, найти соответствующие . Задача: произвести Q единиц выпуска самым дешевым способом, найти соответствующие 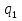 и и 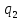 . Формулировка задачи: . Формулировка задачи: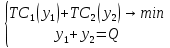 Решение: при оптимальном разделении выпуска между двумя заводами должно соблюдаться равенство Решение: при оптимальном разделении выпуска между двумя заводами должно соблюдаться равенство 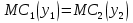 . Докажем это графически: . Докажем это графически: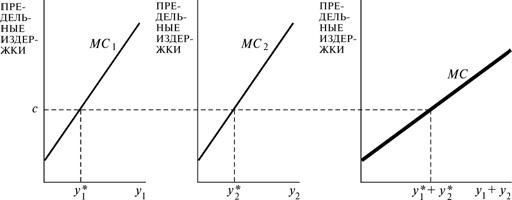 При любом постоянном уровне предельных издержек, скажем c, мы будем производить такие объемы выпуска 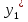 и и 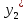 , которые соответствуют равенству MC1( , которые соответствуют равенству MC1(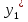 ) = MC2( ) = MC2(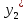 ) = c, и, таким образом, мы произведем ) = c, и, таким образом, мы произведем 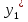 + + 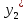 единиц выпуска. Следовательно, объем выпуска, произведенный при любых предельных издержках c, есть просто сумма выпусков, произведенных при условии, что и предельные издержки завода 1, и предельные издержки завода 2 равны c, т.е., результату суммирования по горизонтали кривых предельных издержек. единиц выпуска. Следовательно, объем выпуска, произведенный при любых предельных издержках c, есть просто сумма выпусков, произведенных при условии, что и предельные издержки завода 1, и предельные издержки завода 2 равны c, т.е., результату суммирования по горизонтали кривых предельных издержек.
Предположим, что рынок товара и рынок факторов производства – совершенно конкурентны, при этом цены на продукцию и ресурсы - const. Рассмотрим краткосрочный период, где количество одного из факторов – константа (К) и найдем такой объем другого фактора (L), который максимизировал бы прибыль 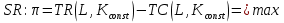 Условие первого порядка: 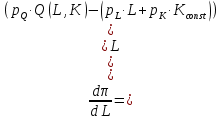 Следовательно, мы получаем необходимое условие первого порядка Следовательно, мы получаем необходимое условие первого порядка 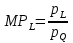 или или 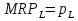 , таким образом, совершенно конкурентная фирма будет тратить ровно столько, сколько будет получать, максимизируя собственную прибыль. Рассмотрим условие второго порядка для максимизации прибыли на рынке ресурсов: , таким образом, совершенно конкурентная фирма будет тратить ровно столько, сколько будет получать, максимизируя собственную прибыль. Рассмотрим условие второго порядка для максимизации прибыли на рынке ресурсов: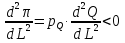 , поскольку мы подразумеваем, что цены положительны, следовательно, , поскольку мы подразумеваем, что цены положительны, следовательно, 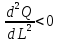 , это значит, что , это значит, что 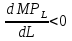 , что есть не что иное, как закон убывание предельной производительности труда. , что есть не что иное, как закон убывание предельной производительности труда.
TC Q Q Q Q* Q** Q1 Q2 MR MC ATC π TR 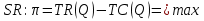 , следовательно, задача сводиться к поиску безусловного экстремума. Рассмотрим необходимое условие первого порядка: , следовательно, задача сводиться к поиску безусловного экстремума. Рассмотрим необходимое условие первого порядка: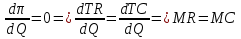 . Однако, данное равенство является условием максимизации прибыли, а не ее минимизации, лишь в том случае, когда выполняется условие второго порядка (достаточное условие): . Однако, данное равенство является условием максимизации прибыли, а не ее минимизации, лишь в том случае, когда выполняется условие второго порядка (достаточное условие): 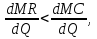 следовательно, следовательно,  . Таким образом, предельные издержки в точке максимизирующей прибыль должны возрастать. Представим графически. Следовательно, при . Таким образом, предельные издержки в точке максимизирующей прибыль должны возрастать. Представим графически. Следовательно, при 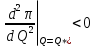 мы получим точку максимума прибыли, а при мы получим точку максимума прибыли, а при 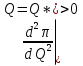 мы найдем минимум прибыли. мы найдем минимум прибыли.
L 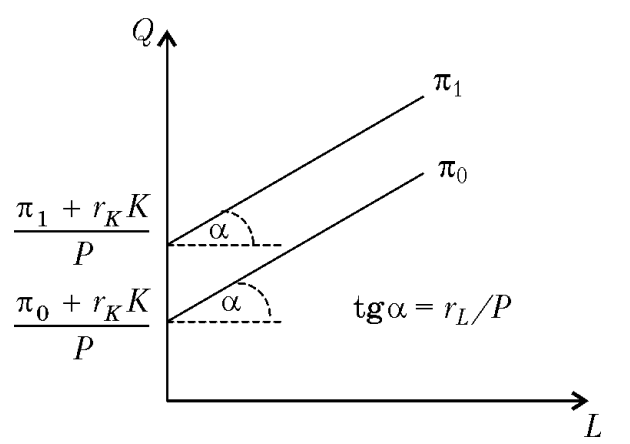 L w L1 L2 L3 SL MRPL MRPL=w w Кривые спроса фирмы на факторы производства показывают взаимосвязь между ценой фактора и максимизирующим прибыль фирмы выбором этого факторы. При заданном оптимальном выборе фактора 2 можно изобразить взаимосвязь между оптимальным выбором фактора 1 и его ценой на графике. Для этого, из условия первого порядка, полученного в билете 17, мы можем выразить функцию спроса на труд 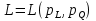 , а если быть более точным, то функция спроса на труд будет иметь следующий вид: , а если быть более точным, то функция спроса на труд будет иметь следующий вид: 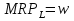 , рассмотрим график. Поскольку до L1 фирма получает отрицательные маржинальные прибыли, а на уровне L3 только выйдет на нулевую прибыль и будет увеличивать количество работников пока MPL>SL, мы будем рассматривать только ниспадающую часть данной кривой, также потому что только в точке L2 достигается максимальная прибыль. , рассмотрим график. Поскольку до L1 фирма получает отрицательные маржинальные прибыли, а на уровне L3 только выйдет на нулевую прибыль и будет увеличивать количество работников пока MPL>SL, мы будем рассматривать только ниспадающую часть данной кривой, также потому что только в точке L2 достигается максимальная прибыль.Также условие 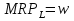 можно получить графически, используя понятие изопрофитных линий – линии постоянной прибыли (см. рис.) можно получить графически, используя понятие изопрофитных линий – линии постоянной прибыли (см. рис.)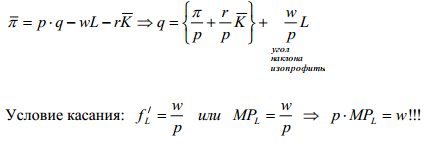

 Если MPL и MPKбудут убывать быстрее, чем убывает перекрестный продукт MPLK, то они будут перекрывать его действие. 
Для того, чтобы вывести функцию предложения фирмы, нужно подставить полученные при задаче максимизации прибыли функции спроса на L и K в производственную функцию: 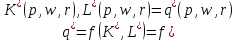 Функция предложения фирмы показывает, какой объем будет производить фирма при данных ценах w,p,r, максимизируя прибыль. LR: 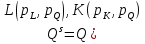 SR: 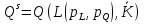
Изменение цены производственного ресурса вызывает поворот изокосты по часовой стрелке (если цена повышается) и против (если цена понижается). 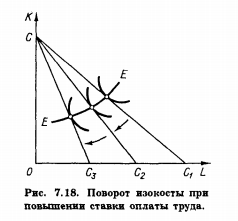 Общий результат изменения йены может быть разложен на эффект замещения и эффект выпуска. 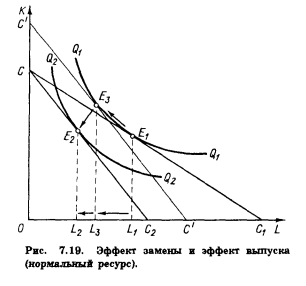 При цене переменного ресурса w1 изокоста занимала положение CC1. После повышения цены до w2 она заняла положение СС2. Общая сумма затрат на ресурсы не изменилась (точка С на оси ординат сохранила свое положение). В результате оптимальная комбинация ресурсов сместилась из точки E1 в точку E2. Общий результат повышения цены переменного ресурса выразился в сокращении объема его применения с L1 до L2. Для разложения этого результата на эффект замены и эффект выпуска проведем параллельно СС2 вспомогательную изокосту  так, чтобы она касалась изокванты Q1Q1(точка касания — E3). так, чтобы она касалась изокванты Q1Q1(точка касания — E3). Как и в теории потребления, мы можем считать, что вдольдуги E1E3 происходит замещение ресурсом К относительно подорожавшего переменного ресурса L при сохранении неизменным объема выпуска Q1Q1. Таким образом, эффект замены составил L1 - L3. Однако, поскольку общая сумма затрат остается неизменной, повышение цены переменного ресурса приводит к сокращению выпуска с Q1 до Q2. а точка, характеризующая оптимальную комбинацию ресурсов, смещается из Е3 в Е2. Это cмещение и характеризует эффект выпуска. В единицах переменного ресурса эффект выпуска составит L3 –L2. Таким образом, общий результат изменения цены переменного ресурса на рис. 7.19 можно разложить на эффект замены и эффект выпуска: L1 – L2 = (L1 – L3) + (L3 - L2) Эффект замены всегда отрицателен, повышение цены ресурса ведет к сокращению, а ее снижение — к увеличению объема применения данного ресурса. Эффект выпуска для нормальных ресурсов также отрицателен, его действие усиливает влияние эффекта замены.
 
Признаки ск: 1) Большое количество фирм 2) Товар однородный 3) Стратегическое поведение фирм отсутствует (нет сговоров и т.д.) 4) Свободные барьеры входа/выхода 5) Совершенная информация 6) Рыночная власть фирм отсутствует Для каждой отдельной фирмы выполняется тождество: MR=P=const 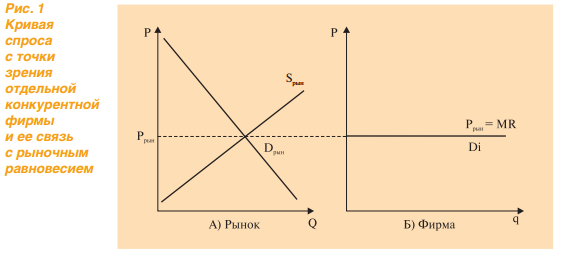 SR: Функция предложения совершенно конкурентной фирмы отражает максимизирующий прибыль выпуск при каждой возможной цене: Q(p) Поэтому функция предложения должна тождественноудовлетворять условию первого порядка максимизацииприбыли:P=MCи условию первого порядка: 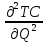 >0 >0 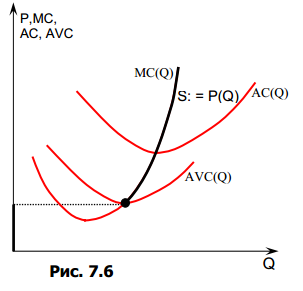 LR:  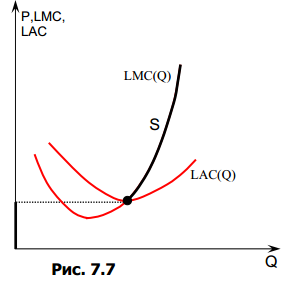
Поскольку по определению совершенной конкуренции доля каждой фирмы на рынке весьма мала, рыночная цена не зависит от объема продукта, продаваемого отдельной фирмой. Это значит, что линия спроса на продукцию данной фирмы - прямая Р = const. параллельная оси абсцисс. Говорят, что спрос на продукцию конкурентной фирмы бесконечно эластичен: при любом, сколь угодно малом, повышении цены по отношению к рыночной объем спроса станет нулевым, а при любом снижении превысит производительные возможности фирмы. Предполагается, что целью фирмы является максимизация прибыли. Произведя продукцию в объеме Q и продавая ее по цене Р, фирма получает выручку в размере РQ и несет затраты TC(Q). Ее прибыль равнаП = PQ - TC(Q). Как мы только что отметили, особенностью функционирования фирмы в условиях совершенной конкуренции является независимость цены от объема выпуска продукции данной фирмы. Условие максимума прибыли имеет вид dП / dQ = P - dTC / dQ = 0, следовательноР = МС. На рис. 1 точки пересечения МС с линиями спроса укажут на тот объем предложения фирмы, который при данной цене обеспечивает максимум прибыли или сводит к минимуму возможные убытки: при цене Р1 это Q1, при цене Р2 это Q2, при цене Р3 это Q3. Продолжая таким образом наблюдать за изменением объема предложения фирмы, стремящейся максимизировать прибыль при изменении цены блага, можно убедиться в том, что кривая предельных затрат устанавливает зависимость объема предложения от цены, т. е. является одновременно и кривой предложения фирмы. MC Q P Q1 Q2 Q3 P3 P2 P1 Рис. 1. Определение выпуска, максимизирующего прибыль фирмы в условиях совершенной конкуренции Этот вывод нуждается, однако, в некоторых уточнениях, для разъяснения которых воспроизведем теперь кривые АТС и AVC, как это сделано на рис. 2. Отметим, что при цене выше Р2 при оптимальном объеме выпуска фирма получает положительную экономическую прибыль, при цене ниже Р3 экономическая прибыль фирмы отрицательна при любом объеме, а оптимальный объем лишь минимизирует убытки фирмы. При цене ниже Р1 выручка фирмы не покрывает переменных затрат и при любом положительном объеме выпуска убытки фирмы будут превышать величину постоянных затрат. Следовательно, оптимальным для фирмы будет решение о прекращении производства, так как нулевой выпуск даст возможность свести убытки к величине постоянных затрат. 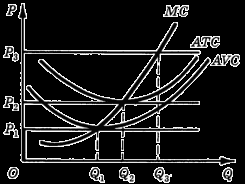 Рис. 2. Линия предложения фирмы в условиях совершенной конкуренция Таким образом, не вся линия МС, а только ее часть над кривой АVС будет представлять график функции предложения фирмы в коротком периоде. Если произвести горизонтальное сложение кривых предложения короткого периода всех фирм, выпускающих одинаковый вид продукции, то получим кривую отраслевого предложения в коротком периоде. Теперь как будто бы есть все данные для того, чтобы узнать, на каком уровне установится цена на рынке совершенной конкуренции: точка пересечения отраслевых кривых спроса и предложения определяет цену блага (Р0 на рис. 3).
Прибыль есть просто разность этих двух площадей. Вспомним наши рассуждения об излишке производителя в гл. 14. Мы определили излишек производителя как площадь слева от кривой предложения по аналогии с излишком потребителя, представленным площадью слева от кривой спроса. Оказывается, излишек производителя тесно связан с прибылью фирмы. Точнее, излишек производителя равен общему доходу за вычетом переменных издержек, или, что то же самое, сумме прибыли и постоянных издержек: Прибыль = py — cv(y) — F Излишек производителя = py — cv.(y). Наиболее непосредственный способ измерения излишка производителя заключается в подсчете разности площади прямоугольника дохода и площади прямоугольника y*AVC(y*), как на рис.21.5A. Однако имеются и другие способы измерения излишка производителя на основе использования самой кривой предельных издержек. 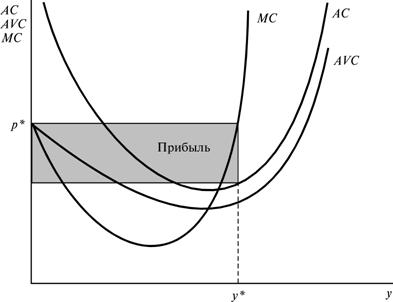
Как мы знаем из гл. 20, площадь под кривой предельных издержек измеряет общие переменные издержки. Это верно, потому что площадь под кривой предельных издержек есть издержки производства первой единицы выпуска плюс издержки производства второй единицы выпуска плюс и т.д. Поэтому чтобы получить излишек производителя, можно вычесть площадь под кривой предельных издержек из прямоугольника общего дохода и получить площадь, представленную на рис.21.5B. Наконец, можно соединить оба способа измерения излишка производителя. Вплоть до точки, в которой предельные издержки равны средним переменным издержкам, можно использовать определение через площадь прямоугольника, а затем воспользоваться площадью над кривой предельных издержек, как показано на рис.21.5C. Этот способ наиболее удобен для большинства приложений, поскольку излишек производителя здесь выступает просто как площадь слева от кривой предложения. Обратите внимание, что этот способ согласуется с определением излишка производителя, данным в гл. 14. 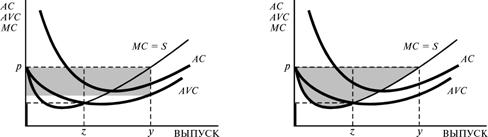 A Общий доход — переменные издержки B Площадь над кривой MC 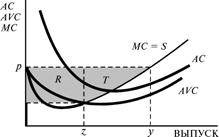 C Площадь слева от кривой предложения
Нас редко интересует общая величина излишка производителя; чаще интерес представляет изменение этого излишка. Изменение излишка производителя при перемещении фирмы из точки выпуска y* в точку выпуска y'обычно представлено трапециевидной областью, изображенной на рис.21.6. 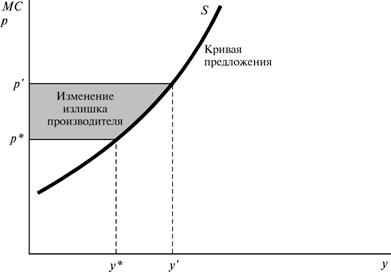
Обратите внимание на то, что изменение излишка производителя при движении от y* до y' есть не что иное, как изменение прибыли при движении от y* до y', поскольку постоянные издержки, по определению, не изменяются. Поэтому влияние изменения выпуска на прибыль можно измерить на основе информации, заложенной в кривой предельных издержек, совершенно не прибегая при этом к кривой средних издержек.  Обратите внимание на то, что изменение излишка производителя при движении от y* до y' есть не что иное, как изменение прибыли при движении от y* до y', поскольку постоянные издержки, по определению, не изменяются. Поэтому влияние изменения выпуска на прибыль можно измерить на основе информации, заложенной в кривой предельных издержек, совершенно не прибегая при этом к кривой средних издержек.
стр 400 вэриан 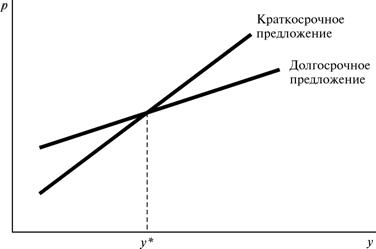 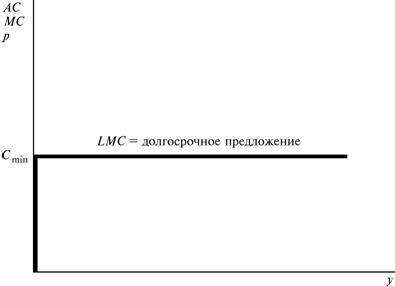 Один из случаев, представляющих особый интерес, — случай, когда в длительном периоде применяемая фирмой технология характеризуется постоянной отдачей от масштаба. В этой ситуации кривая долгосрочного предложения является кривой долгосрочных предельных издержек, которая в случае постоянных средних издержек совпадает с кривой долгосрочных средних издержек. Следовательно, складывается ситуация, изображенная на рис.21.10, в которой кривая долгосрочного предложения представляет собой горизонтальную прямую, проходящую на уровне постоянных средних издержек cmin. Эта кривая предложения означает, что фирма готова предложить любой объем выпуска при p = cmin, произвольно большой объем выпуска при p > cmin и нулевой объем выпуска при p < cmin. Если вспомнить объяснение постоянной отдачи от масштаба с позиций довода о возможности повторения того, что уже было сделано раньше, то сказанное совершенно разумно. Постоянная отдача от масштаба подразумевает, что если вы можете произвести 1 единицу за cmin долл., значит вы можете произвести n единиц за ncmin долл. Поэтому вы готовы будете предложить любой объем выпуска по цене, равной cmin, и произвольно большой объем выпуска по любой цене, большей чем cmin. С другой стороны, если p < cmin, так что вам не удается работать без убытков, даже предлагая одну единицу выпуска, вы, конечно, не сможете работать без убытков, предлагая n единиц выпуска. Следовательно, при любой цене ниже cmin вы захотите предложить нуль единиц выпуска.
Рыночный спрос характеризует общий объем спроса всех потребителей при каждой данной цене данного блага. Суммарная рыночная кривая спроса образуется в результате сложения по горизонтали индивидуальных кривых спроса Зависимость рыночного спроса от рыночной цены определяется посредством суммирования объемов спроса всех потребителей при данной цене. Графический способ суммирования объемов спроса всех потребителей изображен на рисунке 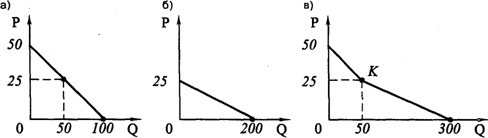 Q1=a1-b1*P Q2=a2-b2*P 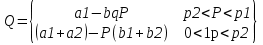 Эластичность - степень реагирования одной переменной величины в ответ на изменение другой, связанной с первой величиной. Эластичность спроса по цене измеряется с помощью коэффициента эластичности. Коэффициент эластичности - это числовой показатель, показывающий процентное изменение одной переменной в результате однопроцентного изменения другой переменной. Эластичность может изменяться от нуля до бесконечности. Значение коэффициента эластичности не зависит от выбора единиц измерения, как по оси функции, так и аргумента. Показатели дуговой эластичности 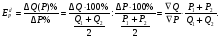 С СB A Q P P2 P1 Q2 Q1 За 100% берутся координаты средней между А и В – точки С. Показатели точечной эластичности Точечный коэффициент обычно применяют в случаях вычисления эластичности в определенной точке или некоторой окрестности точки  Наиболее точное значение можно получить при вычислении эластичности в точке с помощью формулы:  при значительных изменениях объема спроса и цены необходимо использовать формулу, результат которой бы не зависел от направления движения. Этим свойством об ладает коэффициент дуговой эластичности 19. Эластичность спроса, ценовая эластичность Ценовая эластичность заключается : если небольшие изменения в цене приводят к значительным изменениям в количестве покупаемой продукции, то спрос на такие продукты принято называть эластичным; если существенное изменение в цене ведет лишь к небольшому изменению в количестве покупок, то в таких случаях спрос неэластичный. E = |edp|>0, но в силу общего закона спроса edp<0 Классификация спроса по показателю ценовой эластичности Е=+∞ - абсолютно эластичный спрос (совершенно эластичный) Е>1 – эластичный спрос Е=1 – спрос единичной эластичности 0<Е<1 – неэластичный спрос Е=0 – абсолютно неэластичный (совершенно неэластичный) 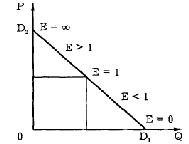 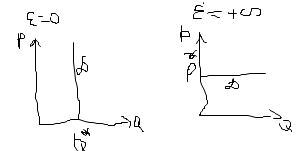 для линейной кривой спроса эластичность спроса по цене – переменная величина. Спрос является
P=a/b P=a/2b Е=(-1) Е=0 Е=- ∞ Эластичный участок кривой спроса Неэластичный участок кривой спроса Q=a Q=a/2 эластичным при 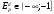 . ерд=dQ/dP*P/Q=-1/P2*P2=-1 . ерд=dQ/dP*P/Q=-1/P2*P2=-1|E|=1 Функция спроса с постоянной эластичностью: 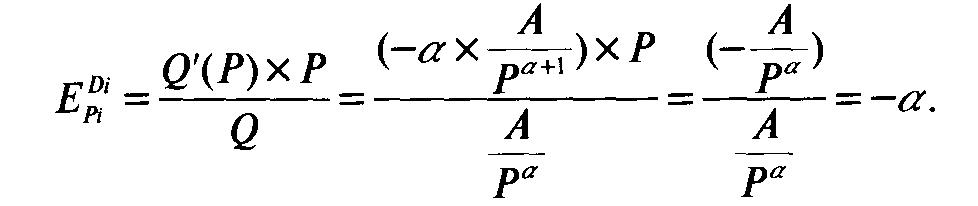 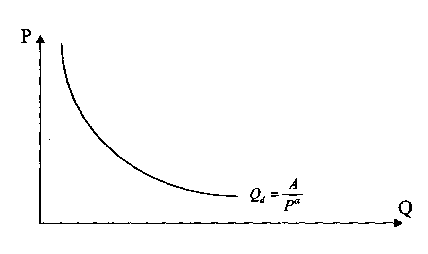 Факторы, определяющие ценовую эластичность спроса.
20. Связь между ценовой эластичностью спроса Эластичность линейной функции спроса изменяется от Изменение эластичности спроса здесь объясняется следующим. Наклон линии спроса в данном случае постоянен. Следовательно, он не совсем точный показатель эластичности. Таким образом, эластичность спроса зависит от соотношения P/Q. dTR/dP = Q(1-ed) Если двигаться вниз по линии спроса, то цена уменьшается, а величина спроса растет, т. е. ed уменьшается. Qd=a-bP a,b>0 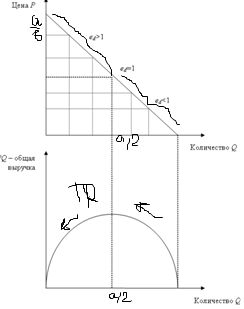 P=a/b – 1/b TR = P*Q=(a/b-1/b*Q)*Q=1/b(a-Q)Q=a/Bq-1/bQ2 Рис. 1. Связь между эластичностью спроса, изменением цены и общей выручкой продавца
Изменяя цену на отрезках с разной эластичностью, фирма может сделать следующие выводы:
Предельная выручка – изменение общей выручки при изменении объема продаж на одну единицу (дискретный случай) или изменение общей выручки при бесконечно малом объеме продаж (непрерывный случай) MR- предельная выручка MR=∆TR/∆Q; MR= dTR/dQ Уравнение пред.выручки в линейном случае: MR=dTR/dQ= (a/bQ -1/bQ2)/Q=a/b – 2/bQ MR= a/b – 2/bQ PD=a/b – 1/b*Q TR=P*Q = P(Q)*Q MR=dTR/dQ*Q+P*Q/Q=P+dP/dQ*Q/P*P=P+1/(dQ/dP*P/Q)*P=P+1/eDP=P(1+1/ eDP)=P(1-1/E) MR=P(1-1/E) Линия MR расположена ниже кривой спроса, поскольку возрастающий объем продукции продается по все более низким ценам (ценам спроса). При ed=1, MR=0, затем TR падает, а MR принимает отрицательные значения. Итак, при ed>1 фирме выгодно снижать цены, но невыгодно повышать. При ed>1 – наоборот: выгодно повышать цены и невыгодно их снижать.
Отраслевое (рыночное) предложение представляет собой объем выпуска, осуществленный всеми фирмами отрасли. Если в отрасли достигнуто равновесие, то объем предложения каждой фирмы отрасли в краткосрочном периоде будет представлен кривой ее предельных издержек. Это означает, что для краткосрочного периода предложение отрасли будет равняться сумме предложения фирм для каждого уровня рыночной цены, а кривая отраслевого предложения является суммой краткосрочных кривых предложения фирм отрасли. 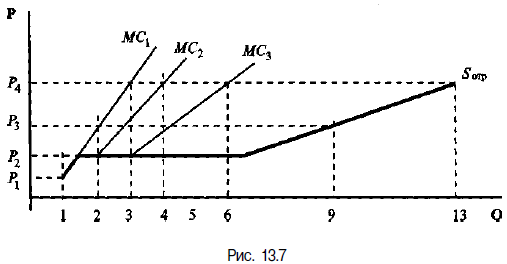 Принцип суммирования кривых предложения фирм для определения кривой отраслевого предложения применим лишь в той степени, в какой цены на используемые в отрасли переменные факторы остаются неизменными. Так как увеличение предложения отрасли приведет к росту спроса на переменные факторы и может вызвать рост цен на них, то в реальной действительности построение кривой отраслевого предложения не сводится к сложению кривых предложения отдельных фирм. Сама же краткосрочная кривая отраслевого предложения будет детерминирована такими факторами, как: количество фирм в отрасли; средний размер фирм отрасли; цены используемых отраслью переменных ресурсов; применяемые в отрасли технологии. Эластичность предложения характеризует реакцию производителя на изменение условий хозяйствования, отражает степень его готовности поставлять на рынок определенный объем товара под воздействием того или иного экономического обстоятельства. В качестве базового показателя эластичности предложения признан коэффициент эластичности предложения по цене. Данный показатель эластичности традиционно определяется как отношение процентного изменения объема предложения (следствие) к процентному (или однопроцентному) изменению цены на данный товар (причина). QS=Q(P) eSP= ∆QS/Q*100% / ∆P/P*100% eSP = ∆QS/∆P * P/QS eSP = dQS/dP * P/QS eS ABP = ∆QS/∆P * P1+P2/Q1S+Q2S случай линейного спроса S1: (+∞;1) – всегда эластичное предложение 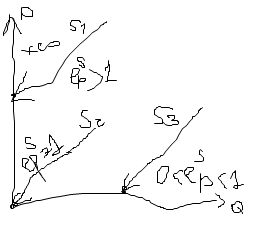 S2: =1 – единичная эластичность S3: (0;1) – всегда неэластичное предложение S1: Q1S = -a +bP, a,b>0 S2: Q2S = bP, b>0 S3: Q3S= a+bP, a,b>0 Степенное предложение QS = c*P , c>0, b>0 epS = dQS/dP = c*b*Pb-1 epS = (c*b*Pb-1) * P/e*Pb = b*Pb-1 *1/Pb-1 = b QS= c*Pb (b>1) 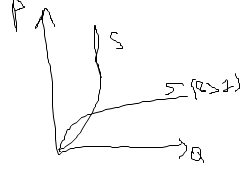
Излишек потребите ля (consumer surplus) CS — разность между рыночной ценой, по которой потребитель приобретает товар, и максимальной ценой, которую потребитель готов заплатить за данный товар. Излишек потребителя пред ставлен ΔPENE, отражающим разность между рыночной ценой товара (PE) и максимальной ценой, по которой потребитель был готов приобрести товар, ограниченную кривой спроса NE. Излишек производителя (producer surplus) PS — разность между текущей рыноч ной стоимостью товара и минимальной ценой, по которой про изводитель готов продать свой товар. Излишек производителя представлен ΔМРЕЕ, являющимся разностью между рыночной ценой товара (РЕ) и минимальной ценой, по которой производи тель был готов продать товар, ограниченной кривой предложе ния ME. На рынке совершенной конкуренции выгоду имеет как по требитель, так и производитель. Общая выгода (W), полу чаемая обществом, будет определяться как сумма излишков по требителя и производителя, т. е. ΔPENE + ΔМРЕЕ. 
Квази – почти. |

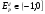 ; нелинейный спрос:
; нелинейный спрос: