Технология как ограничение. Производственное множество и его свойства. Технологически и экономически эффективные способы производства
 Скачать 16.09 Mb. Скачать 16.09 Mb.
|
|
Эффективность конкурентных рынков факторов производства. Граница производственных возможностей. Предельная норма трансформации. кривая (или граница области) производственных возможностей характеризует все множество комбинаций максимальных выпусков двух благ, Xи Y, при полном и эффективном использовании наличных факторов производства, К и L. Любая точка, лежащая выше этой кривой (вне области производственных возможностей), недостижима. Любая точка, лежащая ниже ее (внутри области производственных возможностей), достижима, но неэффективна, она означаетнеэффективноеили неполноеиспользование имеющихся факторов производства (безработицу, наличие неиспользуемых производственных мощностей и т. п.). Такой будет, например, точка S0, соответствующая исходному распределению ресурсов К и L между производством X и Y. 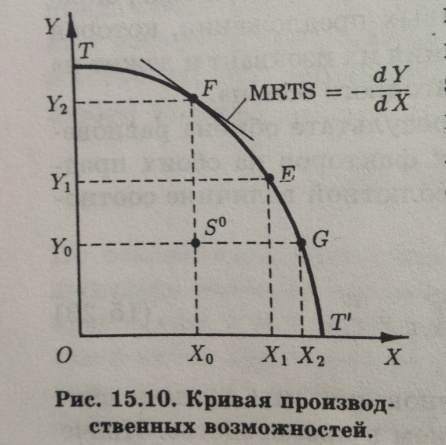 Кривую производственных возможностей (ТТ' на рис. 15.10) можно интерпретировать и иначе. А именно, как кривую продуктовой трансформации. В этой интерпретации кривая продуктовой трансформации показывает, как один продукт Lтрансформируется в другой посредством переключения некоторых факторов с производства одного блага, скажем У, на производство другого, скажемX. Отрицательный наклон кривой продуктовой трансформации характеризуетпредельную норму продуктовой трансформации (MRPT). MRPTX,Yпоказывает, на сколько должно быть сокращено производство блага Y для того, чтобы выпуск блага X увеличился на единицу. MRPTX,Y= -dY/dX. Можно показать, что предельная норма продуктовой трансформации равна соотношению предельных затрат: MRPTX,Y = - dY/dX = MCX/MCY. Выведем это: TC=TC(x;y) dTC= 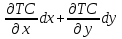 0=MCxdx+Mcydy => - Mcydy= MCxdx =>  В условиях совершенной конкуренции, как мы знаем, цены равны предельным затратам: MCX = PX, MCY = PY Следовательно, наклон кривой производственных возможностей, равный соотношению предельных затрат, в условиях совершенной конкуренции, равен также соотношению цен благ: MRPTX,Y = MCX/MCY = PX/PY
Одна из важных экономических моделей, позволяющая подробнее познакомиться с понятием альтернативных издержек, – кривая про- изводственных возможностей (КПВ) – кривая, каждая точка которой показывает максимальные количества двух экономических благ, которые способна произвести экономика страны при полном и эф- фективном использовании имеющихся ресурсов и текущем уровне технологий. Предпосылки модели КПВ 1. В экономике производится только два товара (вводится для мак- симальной наглядности модели, поскольку дает возможность изоб- разить КПВ на плоскости). 2. Неизменное количество ресурсов. 3. Неизменное качество ресурсов (то есть неизменность их произво- дительности). 4. Неизменный уровень используемых технологий. 5. Полное использование ресурсов (отсутствие известных неисполь- зуемых ресурсов). 6. Эффективное использование ресурсов (отсутствие возможности такого альтернативного распределения ресурсов, которое позволило бы увеличить выпуск одного блага без сокращения выпуска другого). Выполнение предпосылок 4 – 6 обеспечивает отсутствие сдвигов КПВ. Нарушение любого из этих трех утверждений приводит к тому, что произойдет положительный или отрицательный сдвиг КПВ. Выполнение предпосылок 2 и 3 обеспечивает нахождение экономи- ки на КПВ. Нарушение любой из этих двух предпосылок приводит к тому, что экономика страны будет производить комбинацию благ, расположенную «под КПВ» (то есть в условиях неэффективного и/или неполного использования ресурсов). 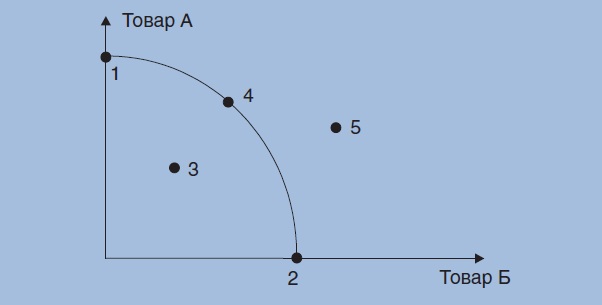 Множество производственных возможностей описывает только технологически допустимое множество выпускаемых товаров. Предельная норма трансформации – то, сколько индивид может получить одного товара, если решит пожертвовать некоторым количеством другого. Кривая, или, как ее иначе называют, граница производственных воз- можностей, показывает точки полного и эффективного использова- ния ресурсов в экономике (например, точка 4 на рис. 5). Точки, находящиеся правее и выше границы производственных воз- можностей, являются недоступными. В настоящее время мы не можем производить такое количество товаров (например, точка 5 на рис. 5). Точки, лежащие под границей производственных возможностей, со- ответствуют ситуациям, когда общество либо не полностью исполь- зует имеющиеся ресурсы, либо неэффективно их использует, либо и то и другое (например, точка 3 на рис. 5). Альтернативные издержки производства некоторого количества одного экономического блага – то количество другого блага, от выпуска которого общество вынуждено при этом отказаться. С математической точки зрения это выразится следующим обра- зом: 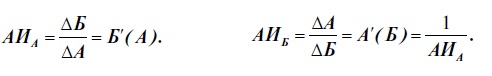 Геометрический смысл альтернативных издержек – это тангенс угла наклона касательной, проведенной в данной точке графи- ка КПВ к положительному направлению оси соответствующего товара. И с математической, и с геометрической точек зрения получаемое значение будет отрицательным, что является отражением слова «от- казаться» в определении альтернативных издержек, поэтому выра- жения «альтернативные издержки производства одной единицы то- вара А равны 3» и «Б′( А ) = −3» эквивалентны. Закон возрастающих альтернативных издержек: при росте про- изводства одного блага выпуск каждой дополнительной единицы этого блага приводит к отказу отвсе большего и большего коли- чества единиц другого блага (то есть, альтернативные издержки производства каждой дополнительной единицы возрастают). Отдача от масштаба (Returns to scale) — это взаимозависимость между изменением масштаба производства и последующим изменением в объеме выпуска продукции. Постоянная отдача от масштаба присутствует тогда, когда при увеличении количества факторов производства в n раз, объем производства, соответственно, также увеличивается в n раз. Возрастающая отдача от масштаба присутствует тогда, когда пропорциональное увеличение количества всех факторов производства в n раз приведет к увеличению объема производства больше чем n раз. Убывающая отдача от масштаба будет иметь место тогда, когда пропорциональное увеличение всех факторов производства в n раз приведет к увеличению объема производства менее чем в n раз. На возрастающую отдачу от масштаба влияют пять факторов.
Факторы, влияющие на постоянную отдачу от масштаба. Увеличение отдачи от масштаба не может длиться бесконечно. Источники, обеспечивающие превышение роста производства над ростом используемых ресурсов, рано или поздно иссякнут. Фактором, вызывающим снижение отдачи от масштаба, является управляемость производства. По мере увеличения фирмы возникает проблема интеграции различных аспектов ее многообразной деятельности. Процесс принятия решений усложняется, а административная нагрузка непропорционально возрастает. Возникает необходимость делегирования полномочий управленцам более низкого уровня, чья компетенция может не соответствовать предъявляемым требованиям. Увеличение масштабов сопровождается расширением формальностей и бумаготворчества; формируются бюрократические процедуры, делающие управленческую иерархию крупных фирм вялой и громоздкой, что ведет к постепенному снижению эффективности.
Предположим, например, что Робинзон может производить в час 10 фунтов рыбы или 20 фунтов кокосов. Тогда, если он уделит Lc часов производству кокосов и Lf часов производству рыбы, то произведет 10 Lf фунтов рыбы и 20 Lc фунтов кокосов. Допустим, что Робинзон решает работать по 10 часов в день. Тогда множество производственных возможностей будет состоять из всех комбинаций кокосов C и рыбы F, таких, что F = 10Lf C = 20Lc Lc + Lf = 10. Первые два уравнения показывают производственные взаимосвязи, а третье — ресурсное ограничение. Чтобы определить границу производственных возможностей, надо найти из двух первых уравнений Lf и Lc: . Теперь, сложив два этих уравнения и воспользовавшись тем фактом, что Lf + Lc = 10, найдем Это уравнение дает нам все комбинации рыбы и кокосов, которые может произвести Робинзон, работая по 10 часов в день. Это множество изображено на рис: 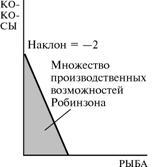
Понятия общего равновесия, эффективности выпуска, теоремы теории благосостояния для экономики, не включающей производство, представлены в вопросах 39-41. Общее равновесие в производстве: Две интерпретации: существует 2 фирмы или фирма производит 2 товара. A: товар «X», технология 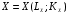 B: товар «Y», технология 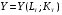 Первоначальное наделение: 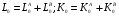 Задача: (максимизируем Х так, чтобы не уменьшался У, с учетом ограничений на ресурсы и цен) 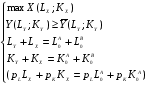 A AB LA LB KA KB LA0 LB0 KA0 KB0 Единственное решение может быть получено, если в экономике есть цены: MRTSLKA=MRTSLKB=PL/PK Уравнение контрактной кривой может быть получено из условия касания производственных функций (MRTSLKA=MRTSLKB): Выразив Ly и Ky через Lx, Kx (используя строки 3 и 4 в системе), мы можем представить это условие как зависимость Kx от Lx, т.е. получить уравнение контрактной кривой Используя условия 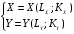 , выразим , выразим 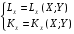 и подставим это в уравнение контрактной кривой. Так мы получим уравнение КПВ (или кривой продуктовой трансформации). При совершенной конкуренции максимальная прибыль от продажи товара Х может быть получена из условия MCx=Px, товара Y - при MCy=Py. Максимальная прибыль в общем может быть получена при соблюдении обоих условий. Это можно записать как и подставим это в уравнение контрактной кривой. Так мы получим уравнение КПВ (или кривой продуктовой трансформации). При совершенной конкуренции максимальная прибыль от продажи товара Х может быть получена из условия MCx=Px, товара Y - при MCy=Py. Максимальная прибыль в общем может быть получена при соблюдении обоих условий. Это можно записать как  . .  соответствует норме продуктовой трансформации (MRPTXY=dY/dXпри ТС=const) соответствует норме продуктовой трансформации (MRPTXY=dY/dXпри ТС=const)Общее равновесие в производстве и потреблении: Объединение условий равновесия в производстве и потреблении. 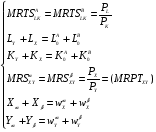 Графически: Y XY X0 Y0 (Внутри КПВ– коробка Эджуорта для потребителя) Первая теорема экономики благосостояния: конкурентное равновесие эффективно по Парето. Неявные предпосылки: отсутствуют внешние эффекты со стороны производства и потребления, конкурентное равновесие существует (исключена возможность возрастающей отдачи от масштаба) Вторая теорема: любое распределения, эффективное по Парето, может быть конкурентным равновесием Предпосылки: предпочтения потребителей и производственные множества фирм непрерывны, монотонны и выпуклы (нет возрастающей отдачи от масштаба) (Доказательства аналогичны приведенным в билетах 40-41; единственное отличие –добавляются ограничения на вид производственных функций) Случай с взрастающей отдачей от масштаба (экономика робинзона крузо): Потребитель и производитель – одно лицо; цена товара (Qc, кокосы)=1, цена труда =w. Тогда прибыль можно посчитать как π=Qc-wL. В координатах Qc, Lможно построить бюджетное ограничение: Qc= π+wL. Труд – антиблаго, кривые безразличия имеют положительный наклон; возрастающая отдача от масштаба=>КПВ (кривая, которая выходит из 0) выпукла вниз Графически: Qc L Кривая, которая касается КПВ – кривая безразличия. Прямая линия – бюджетное ограничение; пересекает ось Qcниже нулевой отметки, значит, прибыль отрицательная (нет оптимума производителя). Точки с положительной прибылью находятся вне производственного множества. Аналитически: возрастающая отдача от масштаба означает, что AC>MC; в совершенной конкуренции максимум прибыли достигается при P=MC=>AC>P. Прибыль можно рассчитать как Q(P-AC), AC>P=>прибыль может быть только отрицательной.
Формулировка теоремы "второго наилучшего"(secondbest) принадлежит Р. Липси и К. Ланкастеру: "Если в систему общего равновесия введено ограничение, которое препятствует достижению какого-либо из условий Парето, то другие условия Парето, хотя и являются все еще достижимыми, как правило, не являются желательными". Экономическая система достигает оптимума (эффективна), когда соблюдаются все условия Парето-эффективности одновременно на всех рынках. Такое состояние именуется как "первое наилучшее" (first best). Но допустим, что в экономической системе появилось неустранимое препятствие, которое не позволяет ей достичь "первого наилучшего". Исходя из общей теоремы о втором наилучшем следует, что "второе наилучшее" (лучшее из возможных в данной ситуации) не достижимо, если будут созданы условия для обеспечения Парето-эффективного состояния везде, где этому не препятствует указанное неустранимое ограничение. |
