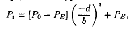Технология как ограничение. Производственное множество и его свойства. Технологически и экономически эффективные способы производства
 Скачать 16.09 Mb. Скачать 16.09 Mb.
|
|
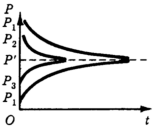
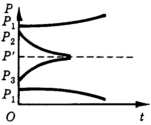
Равновесие может быть устойчивым для всех возможных значений цены (глобальная устойчивость - рис. 7) или только для значений цены в некоторой окрестности Р' (локальная устойчивость - рис. 8).
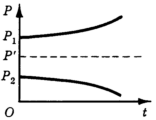
Заметим, что до сих пор мы рассматривали устойчивость как способность цены после некоторого возмущения вернуться к первоначальному значению равновесия Р'. Однако если это возвращение не происходит, то возможны различные случаи: цена неограниченно возрастает или падает (рис. 9), или принимает новое равновесное значение, отличное от Р' (рис. 10)
В этом смысле также говорят иногда об устойчивости равновесия как о способности системы достигнуть состояния равновесия в точке, отличной от первоначального равновесного положения. В экономике, говоря об устойчивости, чаще всего имеют в виду устойчивость первоначального равновесного значения. Перейдем теперь непосредственно к анализу устойчивости рыночного равновесия. Как мы уже знаем, такой анализ требует построения модели, в которой фактор времени был бы учтен явным образом (динамическая модель рынка). Рассмотрим в качестве примера одну из простейших динамических моделей, так называемую паутинообразную модель. Представим себе производителей пшеницы, картофеля или какой-либо иной сельскохозяйственной культуры. Очевидно, что, принимая во время сева решения об объеме производства продукции, они не могут знать цены на эту продукцию в период ее реализации после сбора урожая. В этом случае решения об объеме производства могут основываться только на ожидаемых производителями будущих ценах на их продукцию. Предположим теперь, что производители ожидают в будущем периоде сохранения фактически установившихся в настоящем периоде цен. Тогда объем рыночного предложения товара в каждом периоде зависит от цены этого товара в предыдущем периоде, а объем спроса зависит от уровня цен текущего периода (ведь потребителям нет нужды определять объем закупок заранее, не имея точной информации о ценах):
где QSt - объем предложения товара в период t; Pt-1 - фактическая цена товара в период t-1, QDt- объем спроса товара в период t, Pt - фактическая цена товара в период t. Это значит, что производители определяют в период t — 1 объем предложения следующего периода t, предполагая, что цены периода t - 1 сохранятся и в период t. Такой подход применим, разумеется, не только к сельскому хозяйству, но и к любой отрасли с фиксированным циклом производства. Даже предложение такого специфического товара, как инженеры, зависит, наверное, от заработной платы инженера пять лет назад, когда нынешние выпускники были абитуриентами. Оговоримся сразу, что наша модель поведения производителей (как и любая модель) является некоторым упрощением действительности. Так, мы предполагаем, что производитель, приняв решение об определенном объеме предложения, уже не сможет скорректировать это решение, даже если фактическая цена товара окажется, например, ниже ожидаемой (хотя на самом деле пшеницу можно оставить на поле неубранной, а студент может бросить институт). Мы не предполагаем также возможности образования запасов и их последующей реализации и, уж конечно, не учитываем таких случайных явлений, как естественные колебания урожайности. Однако даже при всех этих допущениях наша гипотеза о поведении производителей, не знающих заранее цены выпускаемого ими товара, представляется довольно правдоподобной, так что интересно посмотреть, к каким выводам относительно устойчивости равновесия приводит основанная на этой гипотезе динамическая модель. Можно показать, что в простейшем случае, при линейных функциях спроса и предложения
и дискретном времени (t = 0,1, 2,.. .Т), уровень рыночной цены в любой момент t определяется уравнением
где Ро — цена в начальный момент (t = 0); РЕ — равновесная цена, при которой QSt = QDt (Как следует из (2), РЕ = = (a-c)/(d + b). Из (3) следует, что рыночная цена Pt будет колебаться вокруг РЕ (поскольку множитель (-d/b)t может быть либо положительным, либо отрицательным). Рыночная цена будет приближаться к равновесной, если (-d/b)t → 0при t → + бесконечности. А это возможно, если \d/b\ <1, или, иначе, если \d\ < \b\. Напротив, если |d| > |b|, рыночная цена будет все более удаляться от равновесного уровня. Наконец, при \d\ = \b\ начальное отклонение рыночной цены от равновесного уровня будет постоянно воспроизводиться. Заметим, что параметры d и Ь характеризуют наклоны линий предложения и спроса. В такой ситуации график спроса и предложения приобретает паутинообразный вид (рис. 11). При этом стабильность равновесия, как видно из рисунка, будет зависеть от абсолютных наклонов линий спроса и предложения. Если абсолютный наклон линии спроса превышает наклон линии предложения, отклонение от равновесия ведет к увеличению колебаний цен и объемов, все более удаляющих рынок от равновесного состояния (рис. 11а). Если абсолютные наклоны линий спроса и предложения одинаковы, всякое первоначальное отклонение ведет к колебаниям цен и объемов одинаковой амплитуды вокруг равновесного Уровня (рис. 11б). Если абсолютный наклон линии предложения выше, чем наклон линии спроса, колебания постепенно затухают, нарушенное равновесие восстанавливается (рис. 11в). 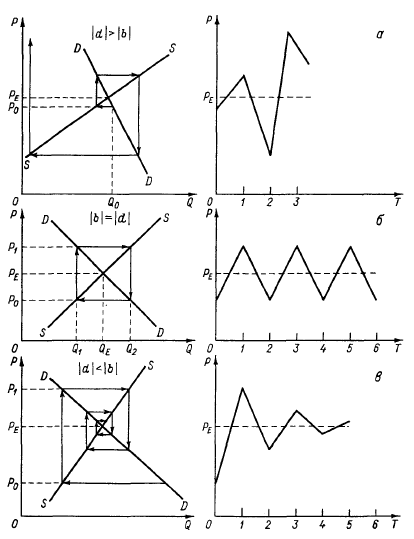 Рис. 11 Паутинообразная модель Рассмотрим подробнее ситуацию, представленную на рис. 116, когда |b| = \d\. Предположим, начальная цена P0. В периоде t= 1 производители, ориентируясь на цену Ро, предложат для продажи продукцию в объеме Q1, что ниже равновесного уровня PE. Возникший дефицит приведет к повышению цены до P1. Предполагая, что этот уровень сохранится и в период t = 2, производители увеличат объем предложения до Q2, что выше равновесного уровня. Избыток предложения приведет к падению цены до Ро и т. д. Заметим, что все три ситуации, представленные на рис. 11, предполагают неизменность функций спроса и предложения во времени. Пусть цена в некоторый начальный период t = 0 была равнаP0 (рис.12), по ней было куплено Q0 единиц товара. Тогда в следующем периоде t = 1 производители выбросят на рынок Q1 единиц товара. Этот объем предложения будет в свою очередь реализован по цене P1 и т. д. (дальнейшее движение не составит труда для читателя). На рис.12 показано, что система стремится к положению равновесия в точке с координатами (P', Q'), т. е. равновесие является устойчивым. 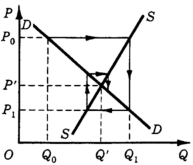 Рис.12 устойчивое равновесие Представим графически динамику изменения цены во времени во всех трех перечисленных случаях (рис. 11). Сформулируем следующие выводы из графического анализа (эти выводы могут быть строго доказаны с помощью математического аппарата разностных уравнений): 1) равновесие является устойчивым, если угол наклона кривой предложения круче угла наклона кривой спроса; 2) равновесие является неустойчивым, с взрывными колебаниями цены, если угол наклона кривой спроса круче угла наклона кривой предложения; 3) цена совершает регулярные колебания вокруг положения равновесия, если углы наклона кривых спроса и предложения равны. Таким образом, теоретически паутинообразная модель предполагает возможность неустойчивости рыночного равновесия. Однако насколько реальна такая возможность на практике? Ведь увидев, что их ожидания постоянно не реализуются, производители наверняка постараются усовершенствовать механизм формирования этих ожиданий. В самом деле, зная динамику изменения цены за несколько предшествующих периодов, можно получить гораздо более точное представление о будущих ценах, чем если просто распространять фактическую цену данного периода на следующий период. Другим стабилизирующим равновесие фактором может послужить образование запасов товаpa и изменение этих запасов (увеличение запасов в одни периоды и уменьшение - в другие).
Экономика, в которой люди имеют постоянный начальный запас товаров и обменивают их, не затрагивая производство, называется экономикой чистого обмена. Коробка Эджуорта представляет собой совмещенные карты безразличия двух индивидов А и В, причем карта безразличия В повернута на 180 градусов, так что начала координат каждой из карт становятся противолежащими вершинами прямоугольника – коробки.  На нижней горизонтальной оси, AXA, откладывается количество блага Х, которым располагает А, на верхней оси BXBколичество того же блага Х, которым располагает B. Аналогично, на левой вертикальной оси AYA откладывается количество блага Y, которым располагает А, так же с индивидом В. Границы коробки Эджуорта соответствуют фиксированным количествам благ X и Y, находящимися в распоряжении индивидов A и В так что AL=BK=XA+XB и AK=BL=YA+YB. Так как количества благ фиксировано, в этой экономике нет производства. Любая точка в пределах коробки Эджуорта характеризует некоторое распределение двух благ X и Y между субъектами А и В. Причем распределяются они без остатка. Поскольку карта кривых безразличия каждого субъекта содержит бесконечное множество кривых безразличия , коробка Эджуорта будет включать и бесконечное множество точек касания кривых безразличия двух субъектов. Это множество образует контрактную кривую. Она представляет все множество взаимоприемлемых результатов обмена двух субъектов. Все точки, через которые проходит контрактная кривая являются Парэто-эффективным распределением двух благ между индивидами. Существует условие эффективности в обмене, которое мы можем сформулировать сразу: блага размещены эффективно, если предельные нормы замены между любыми двумя благами одинаковы для всех индивидов.2 Представим, что происходит обмен двумя благами между индивидами - Андреем и Борисом. Формально условие эффективности в обмене можно записать как 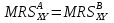 где MRSAXY - предельная норма замены блага Y благом X для Андрея; MRSBXY- предельная норма замены блага Y благом X для Бориса. Любое распределение этих благ между Андреем и Борисом, при котором не выполняется это равенство, является парето-неэффективным (т. е. их благосостояние может быть улучшено). Покажем справедливость этого утверждения. Пусть благо X, имеющееся в количестве 50 ед., и благо Y, имеющееся в количестве 100 ед., распределены между Андреем и Борисом поровну. При этом предельные нормы замены не равны: у Андрея MRSAXY = 2 (он готов отдать 2 ед. X за единицу Y), а у Бориса MRSBXY = 1. Легко заметить, что индивиды могут улучшить свое благосостояние путем обмена. Если взять 1 ед. X у Бориса и передать ее Андрею, забрав у него 2 ед. Y, то благосостояние Андрея не изменится. Если из полученных 2 ед. Y отдать Борису, то его благосостояние тоже останется таким же, как и до обмена. Таким образом, новое распределение (Андрей имеет 26 ед. X и 48 ед. Y, а Борис - 24 ед. X и 51 ед. Y) приносит такое же количество полезности индивидам, что и ранее, но 1 ед. блага Y остается свободной. Если отдать ее Андрею или Борису, то произойдет парето-улучшение и уровень их благосостояния увеличится. Следовательно, первоначальное распределение было неэффективным. Отсюда вытекает, что при любом размещении с разными нормами замены благосостояние может быть увеличено путем перераспределения благ (обмена) между индивидами. Задача заключается в том, чтобы максимизировать полезность одного индивида, скажем А, в то время как полезность другого, B,, принимается фиксированной на постоянном уровне, скажем ÜB . Индивидуальные функции полезности заданы как UA = UA(X,Y), UB= UB(X,Y), Сформируем функцию Лагранжа: Дифференцируя L по Х и Y и приравнивая полученные выражения к нулю, имеем После ряда преобразований и вспомнив теорию потребления, получаем где MU - предельная полезность. В итоге небольших перестановок приходим к следующему результату: (Про КПВ нашла только в лекциях один график) 
Рассмотрим двухпродуктовую двухфакторную модель. Блага Х и У не поступают извне, а производятся двумя фирмами (А и В). В производстве этих благ используются два переменных фактора производства: Kи L (это, кстати, не всегда капитал и труд, бывают другие факторы, но обязательно два!). 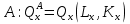 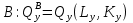 Общее наличие каждого ресурса в экономике:  – начальное наделение трудом – начальное наделение трудом  – начальное наделение капиталом – начальное наделение капиталомПроизводственные функции обоих предприятий в коробке Эджуорта представлены семейством изоквант. 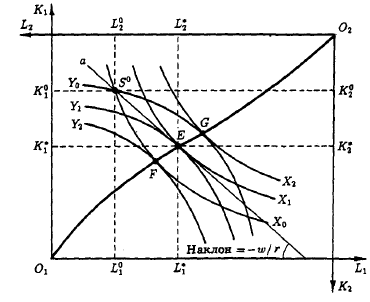 Изокванты в данном случае представляют собой квантифицируемые линии равного выпуска, то есть, каждая из них представляет определенный объем выпуска Х и вторая – объем выпуска Y. Допустим, что начальное распределение Kи L между фирмами А и В, т.е. между производством Х и У отображается т. S0на графике. Как видно из него, начальное распределение факторов не удовлетворяет обе фирмы. В этой точке пересекаются изокванты Х0 и У0, которые имеют разные наклоны,=> предельные нормы замещения (MRTS) факторов К и L оказываются при этом разными. Следовательно, удовлетворять фирмы будет вариант, при котором MRTSXK,L=MRTSYK,L , а это будет происходить во всех точках прямой (контрактной кривой О1О2), проходящей через точки касания изоквант предприятия А и В. Можно определить, какая точка, лежащая на контрактной кривой, будет отражать конечное распределение K и L между фирмами, при котором обмен в распределении прекратиться. Максимальную полезность каждая из фирм получит тогда, когда конечное распределение факторов производства соответствует точке пересечения кривых предложения фирм в коробке Эджуорта. В этой точке (Е) MRTSXK,L=MRTSYK,L=PL/PK(на графике свои обозначения соотношения факторных цен, КСТАТИ НЕПРАВИЛЬНЫЕ, ТАМ ДОЛЖНО БЫТЬ r/w, но суть одна). |