|
|
Сопромат. Реферат по дисциплине Сопротивление материалов
Реферат по дисциплине
«Сопротивление материалов»
2021
Оглавление
Введение
Глава 1. Растяжение – сжатие
Глава 2. Кручение
Глава 3. Геометрические характеристики сечений
Глава 4. Поперечный изгиб балок
Список литературы
Введение
Сопротивление материалов - наука о прочности, жесткости и надежности элементов инженерных конструкций. Методами сопротивления материалов ведутся практические расчеты и определяются необходимые, как говорят, надежные размеры деталей машин, различных конструкций и сооружений.
Сопротивление материалов рассматривает задачи, где наиболее существенными являются свойства деформируемых тел, а законы движения тела, как жесткого целого, не только отступают на второй план, но в ряде случаев являются попросту несущественными.
Дисциплина также имеет целью создать практически приемлемые простые приемы расчета типичных, наиболее часто встречающихся элементов конструкций. Необходимость довести решение каждой практической задачи до некоторого числового результата заставляет в ряде случаев прибегать к упрощающим гипотезам - предположениям, которые оправдываются в дальнейшем путем сопоставления расчетных данных с экспериментом.
Глава 1. Растяжение-сжатие
Растяжением или сжатием называется такой простой вид сопротивления, при котором внешние силы приложены вдоль продольной оси бруса, а в поперечном сечении его возникает только продольная сила.
Для наглядного представления о характере распределения продольных сил по длине стержня строится эпюра продольных сил.
Построение эпюр продольных сил
Правило знаков: растягивающие продольные силы принято считать положительными, а сжимающие – отрицательными. Для определения величины продольной силы N используется метод сечений. Метод сечений позволяет определить внутренние силы, которые возникают в стержне, находящемся в равновесии под действием внешней нагрузки.
Алгоритм решения задач на растяжение (сжатие) методом сечений:
а) Мысленно рассекаем брус сечением n–n на расстоянии х от выбранного начала координат. Начало координат можно помещать в начале каждого грузового участка (местная или локальная система координат) или оставлять в начале стержня (общая или глобальная система координат);
Рисунок 1. Мысленное рассечение бруса сечением n-n
б) Отбрасываем любую часть (рационально отбросить ту часть, на которую действует больше сил или ту, где имеется опора, но опорная реакция еще не определена);
в) Заменяем действие отброшенной части продольной положительной (направленной от сечения, т.е. растягивающей) силой N (х);
Рисунок 2 Замена действия отброшенной части продольной положительной силой
г) Составив уравнение равновесия рассматриваемой отсеченной части, определим величину продольной силы или ее функцию N (х). При этом полученное в результате положительное значение N соответствует растягивающей продольной силе, а отрицательное – сжимающей.
Уравнение равновесия отсеченной части:
Проводя такие сечения в пределах каждого грузового участка, получим функции продольных сил на этих участках.
Примечание: При использовании метода сечений необходимо иметь ввиду, что, если рассматривается равновесие части бруса, включающей в себя опорные связи, необходимо предварительно определить реакции опор, так как они относятся к разряду внешних сил.
Часть бруса, в пределах которой закон изменения внутренних усилий описывается одним аналитическим выражением, называется грузовым участком.
Внешние признаки границ грузовых участков:
места приложения внешних сосредоточенных усилий;
места начала или окончания действия распределенной нагрузки;
места изменения интенсивности распределенной нагрузки;
в случае учета собственного веса бруса – места резкого изменения площади поперечного сечения.
После расчета функции N(x) происходит построение ее графиков в определенном масштабе на грузовых участках. Такие графики и называются эпюрами продольных сил N. Эпюры позволяют определить, в каком сечении действует максимальное внутреннее усилие. Они заштриховываются линиями перпендикулярно к продольной оси бруса, также проставляются знаки (растяжение или сжатие). Каждый штрих в масштабе представляет величину продольной силы N в данном сечении стержня. В случае отсутствия в пределах грузового участка распределенной нагрузки, N=const, т.е. эпюра N на таком участке постоянна.
Рабочее правило для определения величины продольной силы для стержней с прямолинейной осью:
Продольная сила в любом поперечном сечении бруса численно равна алгебраической сумме проекций всех внешних сил, действующих по одну сторону от сечения, на продольную ось бруса в данном сечении.
При использовании этого правила необходимо обязательно учитывать принятое правило знаков для продольной силы.
Глава 2. Кручение
Под кручением понимается такой вид деформации, когда в поперечных сечениях бруса действует только крутящие моменты, а остальные внутренние силовые факторы отсутствуют.
Деформация кручения наблюдается если прямой брус нагружен внешними моментами (парами сил M), плоскости действия которых перпендикулярны к его продольной оси. В чистом виде деформация кручения встречается редко, обычно присутствуют и другие внутренние силовые факторы (изгибающие моменты, продольные силы). Стержни круглого или кольцевого сечения, работающие на кручение, называют валами.
На кручение работают многие детали машин и механизмов, некоторые элементы строительных конструкций. Для вычисления крутящих моментов также используется метод сечений.
Внешние крутящие моменты передаются на вал в местах посадки на него шкивов, зубчатых колес, там, где поперечная нагрузка смещена относительно оси вала. Рассмотрим прямой брус только в состоянии покоя или равномерного вращения. В этом случае алгебраическая сумма всех внешних скручивающих моментов, приложенных к брусу, будет равна нулю. При расчете брусьев, испытывающий деформацию кручения, на прочность и жесткость при статическом действии нагрузки, надо решить две основные задачи: Определение напряжений, возникающих в брусе; Нахождение угловых перемещений в зависимости от внешних скручивающих моментов. При расчете валов обычно бывает известна мощность, передаваемая на вал, а величины внешних скручивающих моментов подлежат определению. Внешние скручивающие моменты, как правило, передаются на вал в местах посадки на него шкивов, зубчатых колес и т.п.
Построение эпюр крутящих моментов Правило знаков: внешний момент вызывает положительный крутящий момент, если со стороны внешней нормали сечения он виден направленным по ходу часовой стрелки.
Для определения напряжений и деформаций вала необходимо знать значения внутренних крутящих моментов Mk (Mz) в поперечных сечениях по длине вала. График, показывающий закон изменения крутящих моментов по длине бруса, называется эпюрой крутящих моментов. Положительные значения на эпюре откладываются вверх от горизонтальной базисной линии, а отрицательные значения – вниз. Зная величины внешних скручивающих моментов и используя метод сечений, можно определить крутящие моменты, возникающие в поперечных сечениях вала.
В простейшем случае, когда вал нагружен только двумя внешними моментами (эти моменты из условия равновесия вала ΣMz=0 всегда равны друг другу по величине и направлены в противоположные стороны), крутящий момент Mz в любом поперечном сечении вала (на участке между внешними моментами) по величине равен внешнему моменту |M1|=|M2|.
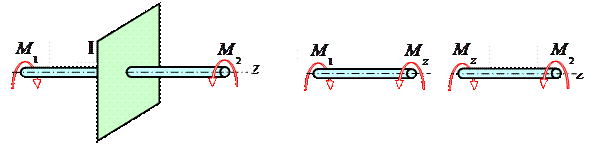
В более сложных случаях, когда к валу приложено несколько внешних моментов, крутящие моменты Mk в поперечных сечениях различных участков вала неодинаковы.
На основании метода сечений крутящий момент в произвольном поперечном сечении вала численно равен алгебраической сумме внешних скручивающих моментов, приложенных к валу по одну сторону от рассматриваемого сечения.
Глава 3. Геометрические характеристики плоских сечений
При расчетах на изгиб, кручение, сложное сопротивление, а также при расчете сжатых стержней на устойчивость используются геометрические характеристики поперечных сечений:
Статический момент площади;
Осевой (экваториальный) момент инерции;
Полярный момент инерции;
Центробежный момент инерции сечения;
Центр тяжести плоского сечения.
Статическим моментом площади относительно некоторой оси называется взятый по всей его площади интеграл от произведения площади элементарного участка dA на расстояние от его центра тяжести до рассматриваемой оси.
Осевым (экваториальным) моментом инерции сечения относительно некоторой оси называется взятый по всей его площади А интеграл от произведения площади элементарного участка dA на квадрат расстояния от его центра тяжести до рассматриваемой оси.
Полярным моментом инерции сечения относительно некоторой точки (полюса) называется взятый по всей его площади А интеграл от произведения площади элементарного участка dA на квадрат расстояния от его центра тяжести до рассматриваемой точки (полюса).
Центробежным моментом инерции сечения относительно некоторых двух взаимно перпендикулярных осей называется взятый по всей его площади А интеграл от произведения площади элементарного участка dA на расстояния от его центра тяжести до рассматриваемых осей.
Центром тяжести плоского сечения является точка, координаты которой вычисляются по формулам:
Статические моменты плоского сечения вычисляются по формулам:
Если оси X и Y являются центральными, то координаты центра тяжести сечения равны нулю. Это значит, что статические моменты относительно центральных осей всегда равны нулю.
Примечания:
Моменты инерции измеряются в см4 и м4.
Осевые и полярные моменты инерции всегда положительны.
Центробежные моменты инерции могут быть положительными, отрицательными или равными нулю.
Центробежный момент инерции сечения относительно осей, из которых одна или обе совпадают с его осями симметрии, равен нулю.
Оси, относительно которых центробежный момент инерции равен нулю, называются главными осями.
Осевые моменты инерции относительно таких осей принимают экстремальные значения и называются главными моментами инерции.
Центральные оси, относительно которых центробежный момент инерции равен нулю, называются главными центральными осями инерции.
Осевой момент инерции сложного сечения относительно оси Z (или Y) равен сумме осевых моментов инерции составляющих его частей (простых фигур) относительно этой же оси.
Центробежный момент инерции сложного сечения относительно некоторых осей Z и Y равен сумме центробежных моментов инерции составляющих его частей (простых фигур) относительно этих же осей.
Для определения моментов инерции сложных сечений в первую очередь их необходимо разбить на простые части и определить моменты инерции простых фигур относительно собственных центральных осей.
Центр тяжести всегда располагается на оси симметрии, если она имеется у сечения.
Глава 4. Поперечный изгиб балок
Изгиб – это такой вид нагружения, при котором стержень загружен моментами в плоскостях, проходящих через продольную ось стержня.
Прямые стержни, загруженные поперечной нагрузкой, в результате своей деформации искривляются. Стержни, работающие преимущественно на изгиб, называются балками. На изгиб работают плиты покрытия и перекрытия, подкрановые балки, ригеля и др.
Чистый изгиб – это такой вид сопротивления, когда в поперечном сечении появляются только изгибающие моменты, а все другие внутренние силы равны нулю. Если в поперечных сечениях действует еще и поперечная сила, то такой вид сопротивления называется поперечным изгибом. Если плоскость действия изгибающего момента содержит одну из главных центральных осей инерции сечения, то изгиб называется плоским или простым.
Построение эпюр поперечной силы и изгибающего момента
При изгибе балки в поперечных сечениях возникают поперечные силы и изгибающие моменты. Для определения внутренних сил снова используется метод сечений.
Правило знаков: Поперечная сила  считается положительной, если она стремится повернуть рассматриваемый элемент балки по часовой стрелке;
Рисунок 3. Правило знаков для поперечной силы Q
Изгибающий момент  считается положительным, если при изгибе элемента балки верхние волокна элемента оказываются сжатыми, а нижние – растянутыми.
Рисунок 4. Правило знаков для изгибающего момента М
Поперечная сила и изгибающий момент определяются из уравнений равновесия отсеченной части балки:
Для того, чтобы произвести расчет балки на изгиб, необходимо знать величину наибольшего изгибающего момента М и положение сечения, в котором он возникает. Точно также, надо знать и наибольшую поперечную силу Q. Для этой цели строят эпюры изгибающих моментов и поперечных сил. По эпюрам легко судить о том, где будет максимальное значение момента или поперечной силы.
Алгоритм решения задач на изгиб методом сечений:
Нахождение опорных реакций, возникающих в закреплении стержня. Если опорные реакции и внутренние усилия можно найти из уравнений статики, то конструкция называется статически определимой. Чаще всего мы встречаемся с тремя видами опорных закреплений стержней: жестким защемлением (заделкой), шарнирно-неподвижной опорой и шарнирно-подвижной опорой. При действии нагрузки в одной плоскости в заделке возникают три опорных реакции (вертикальная, горизонтальная реакции и сосредоточенный реактивный момент); в шарнирно-неподвижной опоре – две реактивные силы; в шарнирно-подвижной опоре – одна реакция – сила, перпендикулярная плоскости опирания.
Балка разбивается на участки, в пределах которых функция внутренней силы не меняет своего аналитического выражения. За границы участков принимаются сечения, в которых приложены внешние нагрузки: сосредоточенные силы, сосредоточенные моменты, начинается или заканчивается распределенная нагрузка одного направления и изменяющаяся по одному закону, а также начало и конец балки.
Последовательно на каждом участке вводится скользящая система координатных осей (начало координат совмещается с началом участка) и для произвольного сечения составляются выражения для определения поперечной силы и изгибающего момента. Затем по этим выражениям в пределах каждого участка строятся графики (эпюры) внутренних сил.
При плоском поперечном изгибе в балке возникают два внутренних усилия: поперечная сила Q и изгибающий момент M. В соответствии с методом сечений поперечную силу можно найти как сумму проекций всех внешних сил, взятых с одной стороны от сечения, на ось, перпендикулярную оси стержня (ось z). Изгибающий момент равен сумме моментов всех внешних сил, взятых с одной стороны от сечения, относительно оси, проходящей через центр тяжести рассматриваемого сечения (оси y).
Список литературы
Вербицкая О.Л, Шевчук Л.И., Зиневич С.И. Учебно-методический комплекс по учебной дисциплине «Сопротивление материалов». 2017 г. – 53 с.
Ф.С. Валиев. Сопротивление материалов. Основы теории и примеры выполнения индивидуальных расчетных заданий: Учебное пособие, часть 1, издание 3 – Новосибирск, 2005 г. – 14 с.; 2005 г. - 75 с.
В. Б. Порошин. Начинаем учить сопромат (Введение в курс сопротивление материалов). Учебное пособие. Челябинск: Издательство ЮУрГУ, 2009 г. – 42 с.
http://www.soprotmat.ru
http://sopromat.vstu.ru
|
|
|
Скачать 86.46 Kb.