ВНД-207 Поляков А.В. Решение задач. Решение Дифференциальный манометр измеряет разность давлений, которая равна
 Скачать 98.98 Kb. Скачать 98.98 Kb.
|
|
Министерство науки и высшего образования РФ Федеральное государственное автономное образовательное учреждение высшего образования «ОМСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» Кафедра «Нефтегазовое дело, стандартизация и метрология» Домашнее задание по дисциплине «Гидравлика и нефтегазовая гидромеханика» _3_ курс, _5_ семестр Выполнил студент гр. ВНД-207 Поляков А.В. Проверил: доц.,к.н. Кожушко А.А. ____________________ Омск, 2022 г. Задача 2.1. Определить разность давлений в сечениях 1 и 2 горизонтального водопровода по разности высот жидкости в трубках ртутного дифференциального манометра, 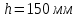 (рис. 1). (рис. 1).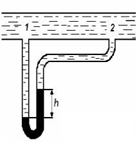 Рис. 1 – Дифференциальный манометр Решение: Дифференциальный манометр измеряет разность давлений, которая равна 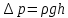 где 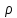 – плотность жидкости, в нашем случае ртути – плотность жидкости, в нашем случае ртути 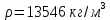 ; ;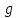 – ускорение свободного падения, – ускорение свободного падения, 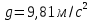 ; ;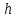 – разность высот жидкости. – разность высот жидкости.Получаем 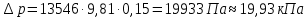 Задача 2.2. Избыточное давление в нефтяном пласте составляет 4,9 МПа. Можно ли предотвратить выброс нефти из скважины, заполнив ее глинистым раствором плотностью 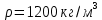 ? Глубина скважины ? Глубина скважины 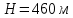 . . Решение: Чтобы выброс нефти не произошел, необходимо чтобы избыточное давление в нефтяном пласте было меньше давления глиняного раствора, которое можно вычислить по формуле 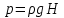 где 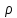 – плотность глиняного раствора; – плотность глиняного раствора;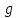 – ускорение свободного падения, – ускорение свободного падения, 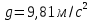 ; ;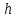 – глубина скважины. – глубина скважины.Получаем 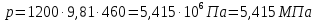 Что больше избыточного давления в нефтяном пласте 4,9 МПа. Таким образом, выброс нефти будет предотвращен. Задача 2.3 На рис. 2 приведен вертикальный разрез газонефтеводоносного пласта, имеющего выход на земную поверхность в точке А. Найти абсолютное давление в газовой шапке, если 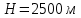 , , 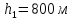 , , 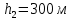 , плотность минерализованной воды , плотность минерализованной воды 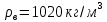 , плотность нефти , плотность нефти 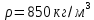 , атмосферное давление 740 мм рт. ст. , атмосферное давление 740 мм рт. ст. 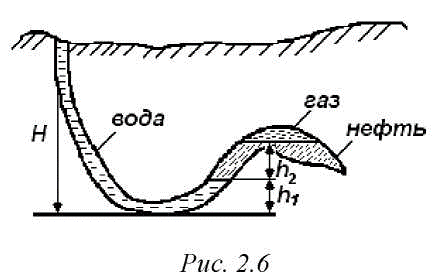 Рис. 2 – Газонефтеводный пласт Решение: Обозначим давление газа в газовой шапке за 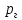 . .Согласно основному уравнению гидростатики давление на границе нефти и воды c одной стороны 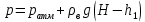 где 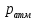 – атмосферное давление; – атмосферное давление;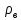 – плотность воды; – плотность воды;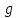 – ускорение свободного падения, – ускорение свободного падения, 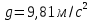 ; ;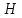 , , 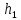 – глубины водяного пласта. – глубины водяного пласта.С другой стороны 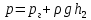 где 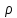 – плотность нефти; – плотность нефти;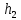 – глубина нефтяного пласта. – глубина нефтяного пласта.Приравнивая, получаем 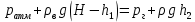 Откуда 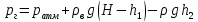 Атмосферное давление задано в мм. рт. ст., т.е. 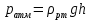 где 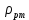 – плотность ртути, – плотность ртути, 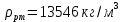 ; ;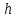 – показания атмосферного давления в мм. рт. ст. – показания атмосферного давления в мм. рт. ст.Получаем 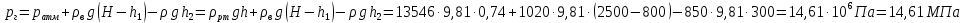 Задача 2.4. Барометр, установленный у подножия холма, показывает давление 760 мм рт. ст., на вершине холма – 720 мм рт. ст. Определить высоту холма, считая температуру воздуха одинаковой и равной 10°С. Газовая постоянная для воздуха 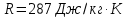 . . Решение: Принимаем воздух за идеальный газ, тогда распределение давления при условии постоянства температуры по высоте описывается барометрической формулой 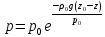 где 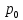 , , 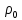 – соответственно абсолютное давление и плотность газа в точках горизонтальной плоскости с координатой – соответственно абсолютное давление и плотность газа в точках горизонтальной плоскости с координатой 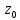 ; ;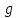 – ускорение свободного падения, – ускорение свободного падения, 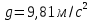 . .Откуда можно найти высоту холма 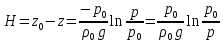 Плотность воздуха может быть вычислена из уравнения Менделеева-Клайперона 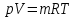 где 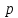 – давление воздуха; – давление воздуха;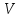 – объем воздуха; – объем воздуха;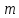 – масса воздуха; – масса воздуха;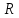 – газовая постоянная воздуха. – газовая постоянная воздуха.Откуда 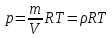 Получаем плотность воздуха 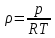 Пренебрегаем изменением плотности воздуха от высоты, и принимаем 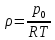 Тогда высота холма 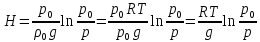 Давления воздуха заданы в мм. рт. ст., т.е. 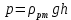 где 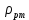 – плотность ртути, – плотность ртути, 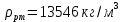 . .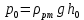 Окончательно получаем высоту холма 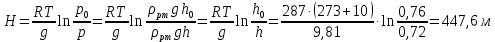 Задача 2.5. Определить, на какой высоте 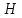 от уровня моря давление воздуха составит 690 мм рт. ст. Температуру воздуха считать постоянной и равной 20°С. Давление воздуха на уровне моря принять соответствующим 760 мм рт. ст. от уровня моря давление воздуха составит 690 мм рт. ст. Температуру воздуха считать постоянной и равной 20°С. Давление воздуха на уровне моря принять соответствующим 760 мм рт. ст. Решение: Опуская выкладки, приведенные в задаче 2.4, приведем сразу полученную формулу для высоты 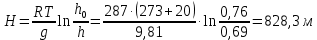 Задача 2.6. Найти силу давления воды на дно сосуда (рис. 3) диаметром 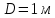 , если глубина , если глубина 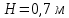 , вес поршня , вес поршня 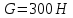 , ,  . .  Рис.3 – Схема сосуда Решение: Согласно основному уравнению гидростатики давление на дно сосуда  где  – избыточное давление, создаваемое весом груза – избыточное давление, создаваемое весом груза 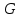 ; ;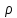 – плотность воды, принимаем – плотность воды, принимаем 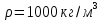 ; ;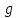 – ускорение свободного падения, – ускорение свободного падения,  ; ; – глубина сосуда. – глубина сосуда.Атмосферное давление можно не учитывать, так как оно действует на все стенки сосуда и груз, и компенсируется. Избыточное давление  где  – площадь верхней части сосуда. – площадь верхней части сосуда.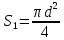 Получаем 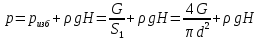 Сила давления воды на дно сосуда 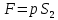 где 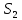 – площадь нижней части сосуда. – площадь нижней части сосуда.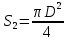 Получим 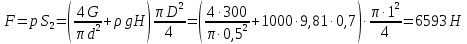 Задача 2.7. Наклонный прямоугольный щит плотины шарнирно закреплен на оси 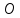 (рис. 4). При каком уровне воды (рис. 4). При каком уровне воды 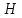 щит опрокинется, если угол наклона щита щит опрокинется, если угол наклона щита  , а расстояние от его нижней кромки до оси шарнира , а расстояние от его нижней кромки до оси шарнира  . Вес щита можно не учитывать. . Вес щита можно не учитывать.  Рис. 4 – Схема щита Решение: Так как атмосферное давление действует на обе стороны щита, то оно взаимно компенсируется, и, следовательно, силы атмосферного давления не учитываем. Поэтому на щит действует только сила давления жидкости. Предполагаем, что силой трения на цапфах щита при повороте можно пренебречь. В соответствии с этим, ось поворота щита должна быть расположена на уровне линии действия силы давления на щит, которая расположена на уровне центра тяжести объема эпюры давления (рис. 5), которая представляет собой треугольник. В этом предельном случае щит еще не опрокидывается. Смоченная поверхность щита   Рис. 5 – Схема щита и эпюры давления Центр тяжести треугольника определяется как точка пересечения его медиан. В случае прямоугольного треугольника на расстоянии одной трети от любого его катета. Тогда  Откуда для опрокидывания щита уровень воды должен быть выше  Задача 2.8. Перед подземным ремонтом газовую скважину «задавили», залив ее ствол до устья (до поверхности земли) водой (рис. 6). Затем в скважину лебедкой спустили насосно-компрессорные трубы, по которым при эксплуатации скважины поступает из пласта газ. Длина спущенных труб – 1000 м, их внешний диаметр – 73 мм, толщина стенок – 5,5 мм, вес одного погонного метра трубы – 93,7 Н. Определить максимальные усилия на крюке лебедки для двух случаев: 1) нижний конец труб открыт; 2) нижний конец труб заглушен.  Рис. 6 – Насосно-компрессорные трубы Решение: Равнодействующая сил давления на цилиндрическую поверхность, складывается из горизонтальных и вертикальных составляющих. Так как труб симметрична и расположена вертикально, то горизонтальные составляющие компенсируются и остается только вертикальная составляющая, которая равна весу жидкости в объеме тела давления (закон Архимеда). 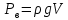 где 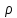 – плотность воды, принимаем – плотность воды, принимаем 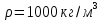 ; ;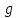 – ускорение свободного падения, – ускорение свободного падения, 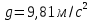 ; ;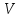 – объем тела давления. – объем тела давления.Кроме этого на лебедку действует сила тяжести самой трубы 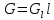 где 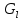 – вес одного погонного метра трубы; – вес одного погонного метра трубы;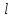 – длина трубы. – длина трубы.Суммарная сила на крюке лебедки 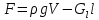 Принимаем что уровень воды расположен точно на уровне труб, то есть глубина погружения труб равна длине труб 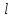 . .1. В случае, когда нижний конец труб открыт, из схемы видно, что тогда труба заполнится водой и объем тела давления 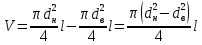 где 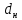 – наружный диаметр трубы; – наружный диаметр трубы;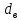 – внутренний диаметр трубы. – внутренний диаметр трубы.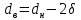 где 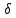 – толщина стенки трубы. – толщина стенки трубы.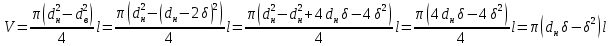 Получаем 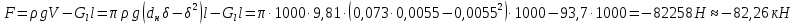 Знак минус означает, что суммарная сила на крюке лебедки направлена вниз, в сторону силы тяжести. 2. В случае, когда нижний конец труб закрыт, из схемы видно, что тогда труба будет заполнена воздухом и объем тела давления 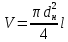 Получаем 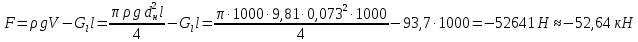 Знак минус означает, что суммарная сила на крюке лебедки направлена также вниз, в сторону силы тяжести. Задача 2.9. Какой объем бензина ( 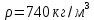 ) можно залить в железнодорожную цистерну внутренним объемом 50 м3 и массой 23 т, чтобы она еще сохраняла плавучесть в пресной воде? ) можно залить в железнодорожную цистерну внутренним объемом 50 м3 и массой 23 т, чтобы она еще сохраняла плавучесть в пресной воде? Решение: Сохранение плавучести в предельном происходит, когда сила тяжести, действующая на цистерну, равна силе Архимеда. При этом цистерна погружена вся в воду, так как плавает в слое воды. Пренебрегаем толщиной стенок, и считаем что внешний объем равен внутреннему. Тогда сила тяжести 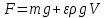 где 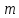 – масса цистерны; – масса цистерны;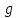 – ускорение свободного падения, – ускорение свободного падения, 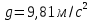 ; ;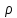 – плотность бензина; – плотность бензина;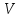 – объем цистерны; – объем цистерны;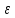 – доля объема цистерны, которая заполнена бензином. – доля объема цистерны, которая заполнена бензином.Сила Архимеда 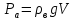 где 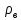 – плотность воды, принимаем – плотность воды, принимаем 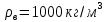 . .Приравнивая получаем 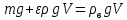 Откуда 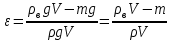 Объем бензина соответственно 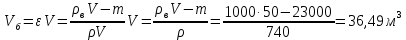 |
