методичка. Решение математических задач в среде Mathcad методические указания к лабораторным работам
 Скачать 2.22 Mb. Скачать 2.22 Mb.
|
ЛАБОРАТОРНАЯ РАБОТА № 2ПОСТРОЕНИЕ ГРАФИКОВ СРЕДСТВАМИ MATHCAD Цель лабораторной работы – ознакомиться с методами созда- ния графиков в среде пакета MathCAD. В пакет MathCAD встроено несколько различных типов графи- ков, которые можно разбить на две большие группы. Двумерные графики: XY (декартовый) график (XY Plot); полярный график (Polar Plot). Трехмерные графики: график трехмерной поверхности (Surface Plot); график линий уровня (Contour Plot); трехмерная гистограмма (3D Bar Plot); трехмерное множество точек (3D Scatter Plot); векторное поле (Vector Field Plot). Все графики создаются совершенно одинаково, с помощью па- нели инструментов Graph (График), различия обусловлены отобража- емыми данными. Построениеграфиковвдекартовойсистемекоординатвоз- можно следующим способом. Вначале необходимо ранжировать аргумент, указав диапазон его изменения и шаг. Это выполняется по правилам, рассмотренным для ранжирования переменных в предыдущей лабораторной работе. Затем надо задать соответствующие функции и ввести шаблон X-Y Plot с помощью меню. Появится шаблон графика с заданной функцией. В средние шаблоны данных нужно поместить имя переменной и име- на функций. Если строятся графики нескольких функций в одном шаблоне, то для их разделения следует использовать запятые. Крайние шаблоны данных служат для указания предельных значений абсцисс и ординат, т.е. они задают масштаб графика. Если оставить эти шаблоны незаполненными, то масштабы по осям графика будет устанавливать- ся автоматически. Чтобы произошло построение графика в автоматическом режиме вычислений, достаточно вывести курсор за пределы графика или нажать клавишу F9. Пример построения графиков показан на рис. 6. x 10 9.99 10 f( x) sin( x)3 x3 f1( x) 1562 f2( x) ex f( x)  f1( x)  1 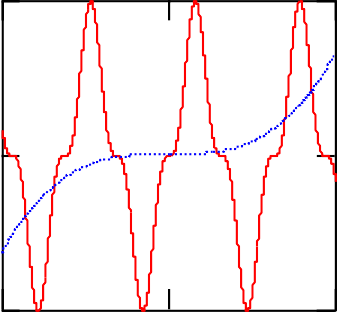 0 1 10 0 10 x f2( x)  Рис. 6 Рис. 64 3 10 2 4 10 1 4 10 0 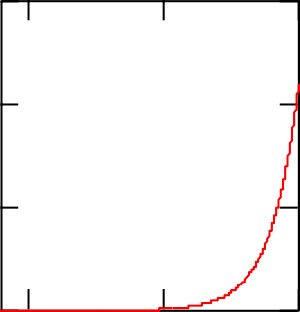 0 5 10 x  Построениеграфиковвполярнойсистемекоординатпроизво- дится углом Wи модулем радиус-вектора R(W). График функции строится в виде линии, которую описывает конец радиус-вектора при изменении угла Wв определенных пределах, чаще всего от 0 до 2 Опция Polar Plot выводит шаблон таких графиков в форме окружно- сти с шаблонами данных. Возможно построение в одном шаблоне двух или нескольких графиков. На рис. 7 показан пример построения графика в полярной системе координат. Построениеграфиковвполярнойсистемекоординатпроизво- дится углом Wи модулем радиус-вектора R(W). График функции строится в виде линии, которую описывает конец радиус-вектора при изменении угла Wв определенных пределах, чаще всего от 0 до 2 Опция Polar Plot выводит шаблон таких графиков в форме окружно- сти с шаблонами данных. Возможно построение в одном шаблоне двух или нескольких графиков. На рис. 7 показан пример построения графика в полярной системе координат.Возможно построение графика в полярной системе координат с использованием шаблона обычного графика в прямоугольной системе координат. Для этого нужно по оси X установить R(W) · cos(W), а по оси Y – R(W) · sin(W). W 0 0.001 2 R1( W ) sin( 3 W ) R2( W ) 1.3 cos ( 5 W ) Rmin 0 Rmax 1.3 R1( W ) R2( W ) 18 240 270 W 0  300 300Рис. 7 Для построения графика поверхности можно воспользоваться двумя способами: Если вам надо только посмотреть общий вид поверхности, то MathCAD предоставляет возможность быстрого построения подобных графиков. Для этого достаточно определить функцию f(x,y) и выпол- нить команду Insert –> Graph –> Surface Plot или нажать соответ- ствующую кнопку наборной панели Graph (сочетание клавиш [Ctrl+7]). В появившейся графической области под осями на месте шаблона для ввода надо указать имя (без аргументов) функции. MathCAD автоматически построит график поверхности. Независимые переменные x и y принимают значения из промежутка [–5,5]. График приведен на рис. 8. 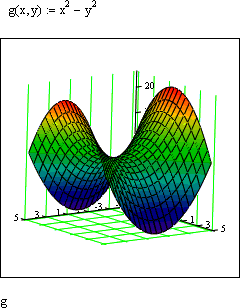 Рис. 8 При необходимости этот промежуток может быть уменьшен или увеличен. Для этого необходимо выделить график и воспользоваться командой Format –> Graph –> 3D Plot или щелкнуть ПРАВОЙ кноп- кой мыши по выделенному графику и в контекстном меню выбрать команду Format. В появившемся окне 3-D Plot Format на вкладке QuickPlot Data (рис. 9) можно установить другие параметры измене- ния независимых переменных x и y. 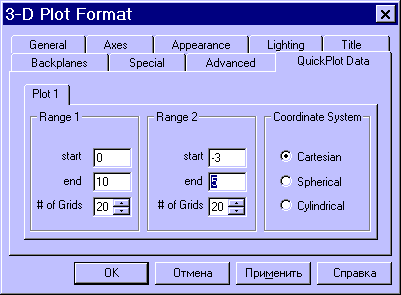 Рис. 9 Для построения графика поверхности в определенной области изменения независимых переменных или с конкретным шагом их из- менения необходимо сначала задать узловые точки xi и yj, в которых будут определяться значения функции. После (а можно и до) этого надо определить функцию f(x,y), график которой хотите построить. После этого необходимо сформировать матрицу значений функции в виде Ai,j = f(xi,yj). Теперь после выполнения команды Insert –> Graph –> Surface Plot в появившейся графической области достаточно ввести имя мат- рицы (без индексов): 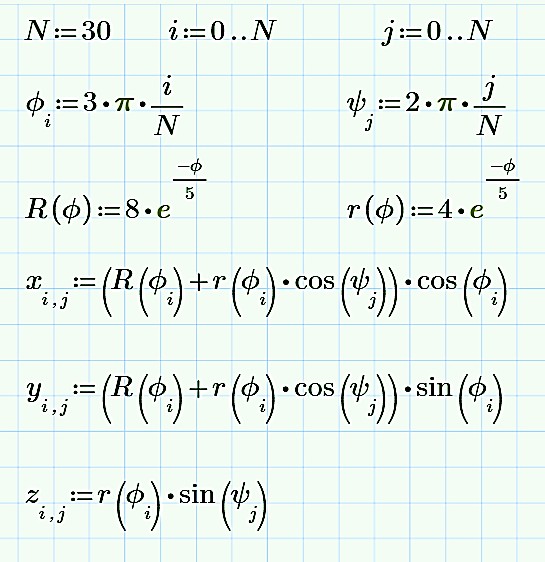 В итоге получим график, изображенный на рис. 10. 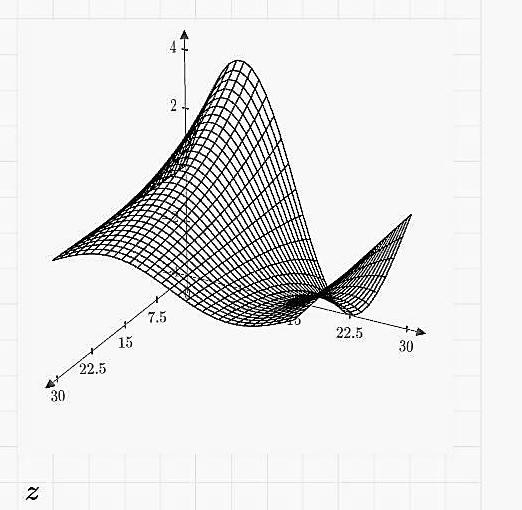 Рис. 10  ПОСТРОЕНИЕ ПОВЕРХНОСТИ          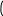  N 20 i 0 N j 0 N xi 1.5 0.15 i yj 1.5 0.15 j N 20 i 0 N j 0 N xi 1.5 0.15 i yj 1.5 0.15 j  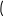  i j  f( x y) sin x2 y2 M f x y f( x y) sin x2 y2 M f x y i j  M Рис. 11 Построение трехмерного графика в виде гистограммы, пред- ставляющей собой трехмерные столбики, высота которых определяет- ся значениями координаты Z(x,y). Подобные графики широко приме- няются при представлении сложных статистических данных, например представленных тремя независимыми переменными. При- мер построения такой гистограммы показан на рис. 12. f(x y) Mx y 2  sin x y sin x yx 0 15 y 0 15 Z)  X Y X Y M Рис. 12 Порядок выполнения работыПостроить график функции в декартовой системе координат. Установить размеры графика не менее 100 × 100 мм. Установить оп- ции «Формат → трассировка», устанавливающие цвет линии – зеле- ный, линия – пунктирная, толщина – 3.    Таблица6 Таблица6
опции «Формат → трассировка», устанавливающие цвет линии – синий, линия – штриховая, толщина – 4. Указать значение периода функции.   Таблица7 Таблица7
 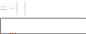 Построить график функции. Модифицировать график, изме- нив его масштаб, включить координатную сетку, обозначить оси ко- ординат. Сохранить все варианты построенных графиков. Построить график функции. Модифицировать график, изме- нив его масштаб, включить координатную сетку, обозначить оси ко- ординат. Сохранить все варианты построенных графиков.y xпри x, изменяющемся в диапазоне от –100 до +100; y x x 1 x 1 при x, изменяющемся в диапазоне от –15 до +15; y до +25; y до +10; y y при x, изменяющемся в диапазоне от –25 при x, изменяющемся в диапазоне от –10 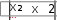 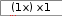 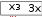 при x, изменяющемся в диапазоне от –5 до +5; при x, изменяющемся в диапазоне от –5 до +5; при x, изменяющемся в диапазоне от –5 до +5; при x, изменяющемся в диапазоне от –5 до +5; y 4 cos4 x sin4 x y 4 cos4 x sin4 xпри x, изменяющемся в диапазоне 2 2 y cos x sin x при x, изменяющемся в диапазоне от –2 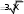 y при x, изменяющемся в диапазоне от –30 до +30; y при x, изменяющемся в диапазоне от –30 до +30;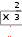 y при x, изменяющемся в диапазоне от –30 до +30. y при x, изменяющемся в диапазоне от –30 до +30. Построить в одной системе координат графики двух функций, обеспечив визуальную возможность их идентификации. Построить в одной системе координат графики двух функций, обеспечив визуальную возможность их идентификации.
y 1 , z  3 2cosx 3 2cosx1 cosx 3 sinx при xот –2 ; y y 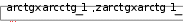 8. 8.arcsinx, z x arcsinxпри xот – ; 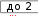 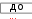  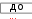 при xот – ; при xот – ;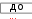 y при xот – ;  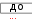 x x x x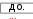 y при xот – ; y при xот – ; yx при xот – 5. Построить график в полярной системе координат. 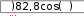 R( R( R( R(для изменяющегося в диапазоне 0  2  для изменяющегося в диапазоне 0 20 для изменяющегося в диапазоне 0 20 3. R( ) cos(2 ) cos2(2 ) 1,3 3. R( ) cos(2 ) cos2(2 ) 1,3для изменяющегося в диапа- 4. R( ) 2 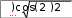 R( R(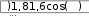 R( R(для изменяющегося в диапазоне 0 20    для изменяющегося в диапазоне 0 для изменяющегося в диапазоне 0 для изменяющегося в диапазоне 0 для изменяющегося в диапазоне 0 7. R( ) cos(2 ) cos2(2 ) 4,5 7. R( ) cos(2 ) cos2(2 ) 4,5для изменяющегося в диа-  пазоне 0 2 ; пазоне 0 2 ;8. R( ) 3e0,1 для изменяющегося в диапазоне 0 20  9. R( ) cos(2 ) cos2(2 ) 0, 01 9. R( ) cos(2 ) cos2(2 ) 0, 01для в диапазоне 0 2 ;  10. R( ) 9 3,6cos( ) для изменяющегося в диапазоне 0 10. R( ) 9 3,6cos( ) для изменяющегося в диапазоне 0 6. Построить график функции Y(x) и исследовать ее поведение в окрестностях точки X0 путем построения еще одного крупномасшаб- ного графика в окрестностях этой точки. 6. Построить график функции Y(x) и исследовать ее поведение в окрестностях точки X0 путем построения еще одного крупномасшаб- ного графика в окрестностях этой точки.
ность описывается выражением влияющие на вид графика. f(x, y) . Изменить опции, 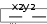 2 3 2 3описывается выражением f(x, y) cos(x3 2 y) . Оформите протокол лабораторной работы средствами MathCAD. Содержание отчетаТитульный лист. Решение всех задач с комментариями. Контрольные вопросыНазовите порядок построения графика в декартовых системах координат. Назовите порядок построения графика в полярной системе ко- ординат. Каким образом можно управлять видом графика, выполняемо- го в декартовой системе координат? 25 Чем определяется количество точек, по которым строится график?  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
