методичка. Решение математических задач в среде Mathcad методические указания к лабораторным работам
 Скачать 2.22 Mb. Скачать 2.22 Mb.
|
ЛАБОРАТОРНАЯ РАБОТА № 5 СИМВОЛЬНЫЕ ВЫЧИСЛЕНИЯЦель лабораторной работы – ознакомиться с основными пра- вилами использования символьного процессора MathCAD. Операции, относящиеся к работе символьного процессора, со- держатся в подменю позиции Symbolics главного меню. Они выпол- няются в командном режиме. Символьные вычисления можно осуществлять в двух различных режимах: с помощью оператора символьного вывода , ключевых слов символьного процессора и обычных формул (рис. 26). Первый способ более удобен, когда требуется быстро получить какой-либо аналитический результат для однократного использова- ния, не сохраняя сам ход вычислений. Второй способ более нагляден, так как позволяет записывать выражения в традиционной математиче- ской форме и сохранять символьные вычисления в документах MathCAD. Кроме того, аналитические преобразования, проводимые через меню, касаются только одного выделенного в данный момент выражения. Соответственно, на них не влияют формулы, находящиеся в документе выше этого выделенного выражения.  Рис. 26 Чтобы символьные операции выполнялись, процессору необхо- димо указать, над каким выражением это должно проводится, т.е. вы- делить выражение. Для ряда операций следует не только указать вы- ражение, к которому она относится, но и наметить переменную, относительно которой выполняется символьная операция. В этом слу- чае само выражение не выделяется, так как ясно, что если маркер вво- да выделяет переменную какого-либо выражения, то это выражение уже отмечено наличием в нем выделяемой переменной. Символьные операции разбиты на пять разделов. Операциисвыделеннымивыражениями. Evaluate – преобразовать выражение с выбором вида преобразо- вания; Evaluate Symbolically – выполнить символьное вычисление вы- ражения; Floating Point Evaluation… – выполнить арифметические опе- рации в выражении результатов в форме числа с плавающей точкой; Complex Evaluation – выполнить вычисления с представлением операций в комплексном виде; Simplify – упростить выделенное выражение с выполнением та- ких операций, как сокращение подобных слагаемых, приведение к общему знаменателю, использование основных тригонометрических тождеств и т.д.; Expand – раскрыть выражение [например для (X+Y)·(X–Y) полу- чим X2 –Y2]; Factor – разложить число или выражение на множители [X2 – Y2 даст (X+Y)·(X–Y); Collect – собрать слагаемые, подобные выделенному выраже- нию, которое может быть отдельной переменной или функцией со своим аргументом (результатом будет выражение, полиномиальное относительно выбранного выражения); Polynomial Coefficients – найти коэффициенты полинома по за- данной переменной, приближающего выражение, в котором эта пере- менная использована. Операциисвыделеннымипеременными. Solve – найти значение выделенной переменной, при которой содержащее ее выражение становится равным нулю; Substitute – заменить указанную переменную содержимым бу- фера обмена; Differintiate – дифференцировать все выражение, содержащее выделенную переменную, по отношению к этой переменной (осталь- ные переменные рассматриваются как константы); Integrate – интегрировать все выражение, содержащее выделен- ную переменную, по этой переменной; Expend to Series – найти несколько членов разложения выраже- ния в ряд Тейлора относительно выделенной переменной; Convert to Practical Fraction – разложить на элементарные дро- би выражение, которое рассматривается как рациональная дробь отно- сительно выделенной переменной. Операциисвыделеннымиматрицами. Они представлены позицией в подменю Matrix, которая имеет свое подменю со следующими операциями: Transpose – получить транспонированную матрицу; Invert – создать обратную матрицу; Diterminant – вычислить детерминант (определитель) матрицы. Операциипреобразования. В позиции меню Symbol содержится раздел операций преобра- зования: Fourier Transform – вычислить прямое преобразование Фурье относительно выделенной переменной (результат – функция от пере- менной s); Inverse Fourier Transform – вычислить обратное преобразова- ние Фурье относительно выделенной переменной; Laplace Transform – вычислить прямое преобразование Лапласа относительно выделенной переменной; Inverse Laplace Transform – вычислить обратное преобразова- ние Лапласа относительно выделенной переменной (результат – функция от переменной t); Z Transform – вычислить прямое z-преобразование выражения относительно выделенной переменной (результат – функция от пере- менной z); Inverse Z Transform – вычислить обратное z-преобразование относительно выделенной переменной (результат – функция от пере- менной n). Стильсимвольныхпреобразований. Evaluation Style – задать вывод результата символьной операции под основным выражением, рядом с ним или вместо него. Все указанные операции можно выполнять двумя способами: непосредственно в командном режиме (используя описанные  выше операции в позиции Simbolic главного меню); выше операции в позиции Simbolic главного меню);с помощью оператора символьных операций представленных в палитре символьных вычислений. операций, На следующей странице приведены примеры использования ре- жимов символьных вычислений. Символьная алгебра.Символьное преобразование. Для его выполнения необходимо выполнить следующие шаги: ввести выражение; окружить его синей выделяющей рамкой; нажать [Shift] [F9] .  Обычно символьный процессор возвращает результаты, пере- страивая переменные. Таким образом, когда Mathcad преобразует вы- ражение, содержащее или e, он будет обычно возвращать другое вы- ражение, содержащее или e. Чтобы предписать Mathcad возвратить числовые значения этих переменных, выберите из меню SIMBOLIC (Символика) Evaluate (Вычислить) Floating point evaluation (С плавающей запятой). Появится диалоговое окно, в котором можно определить число цифр справа от десятичной точки. По умолчанию это число равно 20. Обычно символьный процессор возвращает результаты, пере- страивая переменные. Таким образом, когда Mathcad преобразует вы- ражение, содержащее или e, он будет обычно возвращать другое вы- ражение, содержащее или e. Чтобы предписать Mathcad возвратить числовые значения этих переменных, выберите из меню SIMBOLIC (Символика) Evaluate (Вычислить) Floating point evaluation (С плавающей запятой). Появится диалоговое окно, в котором можно определить число цифр справа от десятичной точки. По умолчанию это число равно 20.Упрощение выражения. Основные алгебраические и тригоно- метрические упрощения выбранного выражения выполняются выбо- ром команды Simplify (Упростить). При этом выполняются арифме- тические преобразования, сокращаются общие множители, используются основные тождества для тригонометрических и обрат- ных функций и упрощаются квадратные корни и степени. Перед вы- бором команды Simplify необходимо выделить синей рамкой упроща- емое выражение или его часть. Упрощению могут быть подвергнуты как все выражения цели- ком, так и его части (например, только числитель дроби). Можно упрощать выражения, содержащие массивы, например, суммы или произведения матриц: 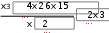 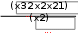 упрощается до упрощается до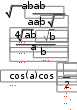  упрощается b упрощается b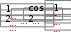 до до1 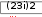 4i3 4i335! упрощается до 2 cos
Разложение выражения. С помощью команды Expend Expres- sion (Разложить по степеням) можно разложить все степени и произ- ведения сумм в выделенном выражении. Если выражение – дробь, числитель будет разложен, и выражение будет представлено как сум- ма дробей. Синусы, косинусы и тангенсы сумм переменных или цело- го числа, умноженного на аргумент, будут разложены, насколько воз- можно, в выражения, включающие только синусы и косинусы одиночных переменных.        ( x 2 y )4 x4 8 x3 y 24 x2 y2 32 x y3 16 y4 ( x 2 y )4 x4 8 x3 y 24 x2 y2 32 x y3 16 y4    sin ( 6 x ) 32 sin ( x ) cos( x )5 32 sin ( x ) cos( x )3 6 sin ( x ) cos( x ) sin ( 6 x ) 32 sin ( x ) cos( x )5 32 sin ( x ) cos( x )3 6 sin ( x ) cos( x )Разложение выражения в ряды позволяет разложить выраже- ние в ряд Тейлора с остаточным членом в форме Пеано. Чтобы ис- пользовать эту команду, необходимо: выделить переменную в функции или выражении, по которой требуется найти разложение; выберите команду Expend to Series (Разложить вряд). При этом диалоговое окно запросит порядок остаточного члена. Это опре- делит число членов формулы. Ответы, которые получаются в результате выполнения этой ко- манды, используют для остаточного члена, обозначенного O. Прежде чем использовать разложение для дальнейших вычислений, следует удалить этот остаточный член:  ex a exp(   a ) exp( a ) exp(a ) x 1 2 exp( a ) x2 1   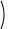 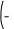 6 exp( a ) x3 O( x4 )     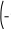 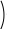 Разложения выражения на множители. Использование коман- ды Factor Expression (Разложить на множители) позволяет разложить выражение на множители выбранное выражение. Если выражение представляет собой целое число, то Mathcad будет пытаться преобра- зовать выражение в произведение. Эта команда будет объединять сумму дробей в одну дробь и будет упрощать многоэтажную дробь с несколькими дробными чертами. Разложения выражения на множители. Использование коман- ды Factor Expression (Разложить на множители) позволяет разложить выражение на множители выбранное выражение. Если выражение представляет собой целое число, то Mathcad будет пытаться преобра- зовать выражение в произведение. Эта команда будет объединять сумму дробей в одну дробь и будет упрощать многоэтажную дробь с несколькими дробными чертами.Приведение подобных членов. Для объединения членов, со- держащих одинаковые степени выделенного подвыражения, необхо- димо пользоваться командой Collect Subexpression (Разложить по подвыражению). Выбираемое подвыражение должно быть простой переменной, либо встроенной функцией вместе с аргументом. Разложение на элементарные дроби. Для того, чтобы преобра- зовать выражение в сумму элементарных дробей, необходимо: выделить переменную в знаменателе выражения; выбрать команду Convert to Partial Fraction (Разложить на элементарные дроби): 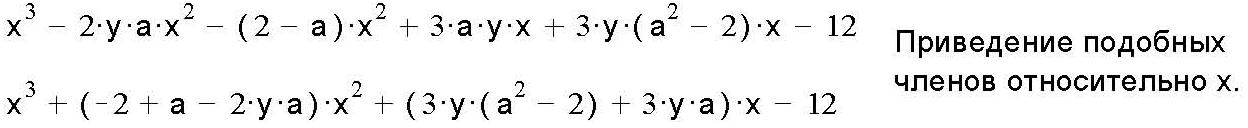  x y ( x y )2 1 x y ( x y )2 1    factor x factor x   x2 y2 x2 y2375849581 x4 y4 ( 89) ( 4223029) ( y x )  a2 x3 2 x a2 x3 2 x    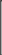   ( a 1 ) x 3 a 3 a ( a 1 ) x 3 a 3 a  3 a 3 a0  a2 a2Нахождение коэффициент относительно степеней x.   6 sin ( x ) 6 sin ( x )( sin ( x ) )2 ( 2 a ) sin ( x )   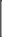 0   8 a Нахождение коэффициентов 8 a Нахождение коэффициентов1 относительно степеней sin x. При этом символьный процессор будет пытаться разлагать зна- менатель выражения на линейные или квадратичные множители, имеющие целочисленные коэффициенты. Если это удается, он будет разлагать выражение в сумму дробей с этими множителями в качестве знаменателя. Все константы в выделенном выражении должны быть целыми числами или дробями. Mathcad не будет разлагать выражение, которое содержит десятичные точки. Нахождение коэффициентов полинома. Для того, чтобы вы- ражения перезаписать в виде полиномов от выделенной переменной или относительно подвыражения, необходимо: выделив переменную или функцию, относительно которой требуется разложить выражение в полином; выбрать команду Polynomial Coefficients (Полиномиальные коэффициенты):   5 x2 3 x 10 23 5 x2 3 x 10 23    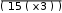 x3 2 x2 9 x 18 x3 2 x2 9 x 1832 36    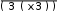 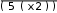 Mathcad возвращает вектор, содержащий коэффициенты требуе- мого полинома в порядке возрастания степеней. Замена переменных. Для замены выделенным выражением за- данной переменной необходимо: выделить выражение, которое будет заменять переменную; скопировать его в буфер обмена, выбирая команду Copy (Ко- пировать) из меню Edit (Правка); выделить переменную, которую нужно заменить, и выбрать Substitute for Variable (Заменить переменную) из меню Symbolic. Вычисление сумм и произведений. Для вычисления суммы необходимо: вызвать оператор суммирования; ниже « »; окружить все выражение выделяющей рамкой и нажать [Shift] [F9]:n         3 n 2 13 ( n 1 )2 3 ( n 1 )3 1 ( n 1 )4 3 n 2 13 ( n 1 )2 3 ( n 1 )3 1 ( n 1 )4    a = 1 a = 1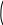 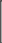  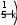 10 10  1k = 1 4 2 4 131269138 244140625 Символьные вычисленияПроизводные. Чтобы вычислить производную в символьном виде, можно использовать оператор производной Mathcad: задайте оператор первой производной или производной более высокого порядка; в поле введите выражение, которое требуется дифференциро- вать, и переменную, по которой дифференцируете; нажмите [Shift] [F9]. Производную можно найти, не используя оператор производной: выделите переменную, по которой необходимо произвести дифференцирование; выберете команду Differentiate on Variable (Дифференциро- вать по переменной). Неопределенные интегралы. Для использования символьного оператора вычисления неопределенного интеграла:      d ( sin ( x ) cos( x ) ) d x d ( sin ( x ) cos( x ) ) d xcos( x ) sin ( x ) Нахождение производной. 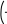 Нахождение второй производной и упрощение выражения для второй произво Нахождение второй производной и упрощение выражения для второй произво 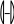 sin 1 sin 1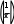 d 2 x d 2 xcos 1 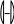 x sin 2 cos 1 x   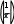 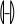 x   sin 2 sin 2  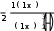 d x 2 d x 2x4 x3 x4    1 x 1 1 x 1 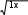 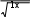 Нахождение производной без применения оператора производной.  вставьте оператор неопределенного интеграла и поля ввода его параметров; заполните поле ввода для подынтегрального выражения; поместите переменную интегрирования в поле ввода, следую- щее за «d»; заключите выражение в выделяющую рамку; нажмите [Shift] [F9]: 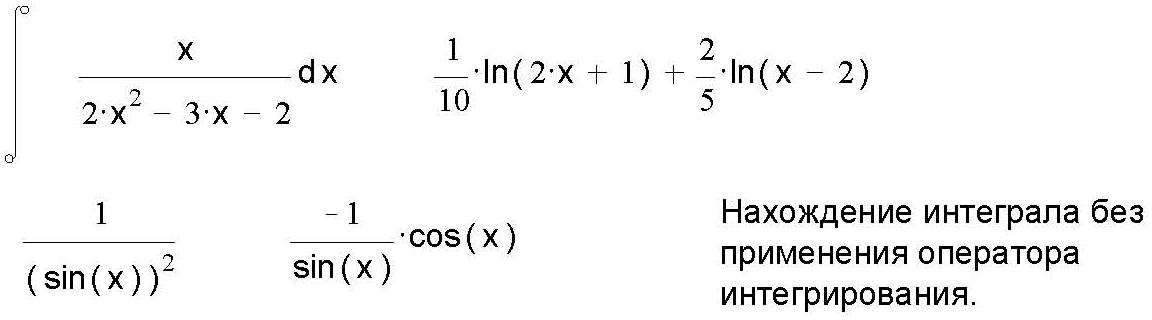 Возможно интегрирование без использования символьного опе- ратора вычисления неопределенного интеграла. Для этого: выделите переменную, по которой ведется интегрирование; выберете пункт меню Integrate on Variable (интегрировать по переменной). Определенные интегралы. Для использования символьного оператора вычисления определенного интеграла: введите знак определенного интеграла с пустыми полями ввода; заполните поля ввода для пределов интегрирования. Они могут быть переменными, константами или выражениями; введите в поле ввода подынтегральное выражение; заполните поле ввода позади «d». Это задаст переменную инте- грирования; нажмите [Shift] [F9]: 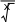   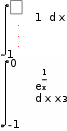 2 exp( 1 ) 2 exp( 1 ), процессор выдает точное значение интеграла. Если подынтеграль- ное выражение или один из пределов содержит десятичную точку, символьный ответ будет числом, отображаемым с двадцатью знача- щими цифрами. Пределы. В Mathcad PLUS есть три оператора вычисления пре- делов. Они могут быть вычислены только символьно. Чтобы исполь- зовать операторы, вычисляющие пределы, необходимо: вызвать оператор нахождения соответствующего предела; ввести выражение в поле ввода справа от lim; ввести переменную, по которой вычисляется предел, в левое поле ввода ниже lim; ввести значение предела в правое поле ввода ниже lim; заключить выражение в выделяющую рамку; нажать [Shift] [F9].     3 3 3 3    lim ( x 1 )2 ( x 1 )2 0 lim ( x 1 )2 ( x 1 )2 0x ex 1  lim +  x e x elim -  x e x e  x e x e ex 1 ex 1  x e x eСимвольное решение уравненийРешение уравнения относительно переменной. Для этого: напечатайте уравнения, используя для ввода знака равенства символ = (вводится нажатием комбинаций клавиш [Ctrl] =); выделите переменную, относительно которой нужно решить уравнение; выберите функцию меню Solve on Variable (решить относи- тельно переменной).  Mathcad решит уравнение относительно выделенной переменной и вставит результат в рабочий документ. Если переменная возводи- лась в квадрат в первоначальном уравнении, при решении можно по- лучить два ответа. Mathcad отображает их в виде вектора. Mathcad решит уравнение относительно выделенной переменной и вставит результат в рабочий документ. Если переменная возводи- лась в квадрат в первоначальном уравнении, при решении можно по- лучить два ответа. Mathcad отображает их в виде вектора.Можно решать неравенства, использующие символы <, >, и Решения для неравенств будут отображаться в терминах булевых вы- ражений Mathcad. Если имеется более одного решения, Mathcad по- мещает их в вектор. В Mathcad булево выражение типа x< 2 имеет значение 1, если оно истино, и 0 – если оно ложно. Таким образом, решение «x– меньше, чем 2, и больше, чем –2» можно было бы пред- ставить выражением (x< 2)·(–2 < x):   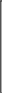   sin ( 3 x ) cos( 2 x ) sin ( 3 x ) cos( 2 x )2  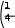 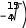 10 10   asin asin   x3 5 x2 8 x 4 0 x3 5 x2 8 x 4 0( x 2 ) ( 1 x ) Нахождение корней уравнения. Для этого: напечатать выражение; выделить в любом месте переменную, относительно которой уравнение решается; выбрать пункт Solve on Variable (Решить относительно пере- менной):   3 x2 5 x 6 3 x2 5 x 6 5 1 97   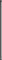  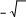 6 6 6 6  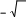 5 1 97 5 1 976 6 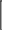   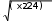 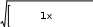 0    x 1 5 x 1 5Обратите внимание, что нет никакой необходимости приравни- вать выражение нулю. Если Mathcad не находит знака равенства, он предполагает, что требуется приравнять выражение нулю. Порядок выполнения работыВойти в систему MathCAD. Внимательно ознакомиться с опи- санием лабораторной работы. Выполнить некоторые рассмотренные примеры. После завершения изучения описания удалить с листа рас- смотренные примеры. Выполнить средствами пакета MathCAD последовательность заданий из вариантов, указанных преподавателем, формируя единый до- кумент. Каждую задачу обязательно сопровождать комментариями. Выполнить задание 1. Выполнить задание 2. Выполнить задание 3. Выполнить задание 4. Выполнить задание 5. Выполнить задание 6. Выполнить задание 7. Выполнить задание 8. Решить в символьной форме квадратное уравнение для свое- го варианта из п. 2.2. лабораторной работы № 1. Оформить отчет. |

