методичка. Решение математических задач в среде Mathcad методические указания к лабораторным работам
 Скачать 2.22 Mb. Скачать 2.22 Mb.
|
ЛАБОРАТОРНАЯ РАБОТА № 6РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ Цель лабораторной работы – ознакомиться с основными прие- мами решения дифференциальных уравнений и систем уравнений численными методами. Обыкновенные дифференциальные уравненияДифференциальные уравнения – это уравнения, в которых неиз- вестными являются не переменные (т.е. числа), а функции одной или нескольких переменных. Эти уравнения (или системы) включают со- отношения между искомыми функциями и их производными. Если в уравнения входят производные только по одной переменной, то они называются обыкновенными дифференциальными уравнениями (ОДУ). В противном случае говорят об уравнениях в частных произ- водных. Решить дифференциальное уравнение – значит, определить неизвестную функцию на определенном интервале изменения ее пе- ременных. Одно обыкновенное дифференциальное уравнение или система ОДУ имеет единственное решение, если помимо уравнения опреде- ленным образом заданы начальные или граничные условия. В курсе высшей математики доказываются теоремы о существовании и един- ственности решения в зависимости от тех или иных условий. Одним из типов задач, которые возможно решать с помощью MathCAD, яв- ляются так называемые задачиКоши, для которых определены начальные условия на искомые функции, т.е. заданы значения этих функций в начальной точке интервала интегрирования уравнений. Решение ОДУ первого порядкаДифференциальное уравнение первого порядка может по опре- делению содержать помимо самой искомой функции y(t) только ее первую производную y(t) . В подавляющем большинстве случаев 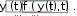 дифференциальное уравнение можно записать в стандартной форме (форме Коши) Только с такой формой умеет работать вычислительный процес- сор MathCAD. Правильная с математической точки зрения постановка соответствующей задачи Коши для ОДУ первого порядка должна по- мимо самого уравнения содержать одно начальное условие – значение функции y(t0 ) в некоторой точке t0 . Требуется явно определить функцию y(t) на интервале от t0 до t1 .  Решение ОДУ первого порядка с помощью вычислительного блока Given/Odesolveсостоит из трех частей: Решение ОДУ первого порядка с помощью вычислительного блока Given/Odesolveсостоит из трех частей:Given – ключевое слово;  ОДУ и начальное условие, записанное с помощью логических ОДУ и начальное условие, записанное с помощью логическихоператоров, причем начальное условие должно быть в форме y(t0 ) Odesolve (t, t1) – встроенная функция для решения ОДУ отно- сительно переменной tна интервале ( t0 , t1 ).  Пример решения ОДУ первого порядка y посред- Пример решения ОДУ первого порядка y посред-ством вычислительного блока приведен на рис. 27. Given  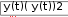 d y(t) d y(t)dt  y(0) 0,1 y(0) 0,1y: Odesolve(t,10) Иллюстрируем решение уравнения графиком. y(t) 1 0.8 0.6  0.4 0.40.2 0  2 4 6 8 10 t Рис. 27 Решение системы ОДУ первого порядкаВ MachCAD имеется встроенная функция rkfixed( y0 , t0 , t1,M,D), которая позволяет решать задачу Коши методом Рунге – Кутты с фик- сированным шагом, где: y0 – вектор начальных значений в точке t0 размера N× 1; t0 – начальная точка расчета; ние; t1 – конечная точка расчета;  M – число шагов, на которых численный метод находит реше- M – число шагов, на которых численный метод находит реше-D – векторная функция размера N× 1 двух аргументов – ска- лярного tи векторного y. При этом y– искомая векторная функция ар- гумента t того же размера N × 1. Функция выдает решение в виде матрицы размером (M× 1) ×  × (N×1). В ее левом столбце находятся значения аргумента t, делящие интервал на равномерные шаги, а в остальных столбцах – значения × (N×1). В ее левом столбце находятся значения аргумента t, делящие интервал на равномерные шаги, а в остальных столбцах – значенияискомых функций y0 (t), y1(t), рассчитанные для этих значений аргумента. Поскольку всего точек (помимо начальной) M, то строк в матрице решения будет всего M+1.  Рассмотрим пример решения системы уравнений с начальным условиями x(0) = 0,1 и y(0) = 0 при количестве шагов M = 100. Текст программы приведен на рис. 28.     2 y0 4 y1 2 y0 4 y1 0.1 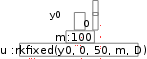  ( y)0 3 y1 ( y)0 3 y1 Рис. 28 При оформлении первой строки программы, в которой опреде- лена система ОДУ, необходимо сравнить запись исходной системы уравнений и формальную запись в MathCAD. Это поможет вам ис- ключить возможные ошибки. Функция D, входящая в число парамет- ров встроенной функции для решения ОДУ, должна быть обязательно функцией двух аргументов. Второй ее аргумент должен быть векто- ром того же размера, что и сама функция D. Точно такой же размер должен быть и у вектора начальных значений второй строке листинга). y0 (он определен во Надо помнить, что векторную функцию D(t.y) следует опреде- лять через компоненты вектора y с помощью кнопки нижнего индекса (Subscript) с наборной панели Calculator. В третьей строке листинга определено число шагов, за которое рассчитывается решение, а его последняя строка присваивает матричной переменной uрезультат действия функции rkfixed. Решение системы ОДУ будет осуществлено на промежутке (0,50).
Матрица решений системы уравнений приведена на рис. 29. u Рис. 29 Размер полученной матрицы будет равен (M × 1) × (N × 1), т.е. 101 × 3. График, иллюстрирующий решение системы ОДУ, приведен на рис. 30. Обращает на себя внимание необходимость отдельного за- дания диапазона значений аргумента для лучшего отображения обла- сти решения системы.  1 10 3 1 10 35 10 4  u  0    5 10 4 1 10 3  10 20 30 40 50 10 20 30 40 50u Рис. 30 ОДУ высшего порядкаОбыкновенное дифференциальное уравнение с неизвестной функцией y(t), в которое входят производные этой функции вплоть до yN(t), называется ОДУ N-го порядка. Если имеется такое уравнение, то для корректной постановки задачи Коши требуется задать Nначальных условий на саму функцию y(t) и ее производные от первого до (N– 1)-го порядка включительно. В МathСАD можно решать ОДУ высших порядков с помощью вычислительного блока Given/Odesolve. Внутри вычислительного блока:  ОДУ должно быть линейно относительно старшей производ- ной, т.е. фактически должно быть представлено в стандартной форме; ОДУ должно быть линейно относительно старшей производ- ной, т.е. фактически должно быть представлено в стандартной форме;начальные условия должны иметь форму а не более сложную. y(t) или yN(t) = b, В остальном решение ОДУ высших порядков ничем не отлича- ется от решения уравнений первого порядка, что иллюстрируется рис. 31. Given    y(0) 0. y'(0) 0 y(0) 0. y'(0) 0дифференциальное уравнение  d2 y(t) dt2 d2 y(t) dt20.1 d y(t) dt   1 y(t) 0 1 y(t) 0начальные условия y Odesolve(t 50)  0.1 0.10.05  y(t) 0   10 20 30 40 50 10 20 30 40 50t Рис. 31 Порядок выполнения работыВойти в систему MathCAD. Внимательно ознакомиться с опи- санием лабораторной работы. Выполнить некоторые рассмотренные примеры. После завершения изучения описания удалить с листа рас- смотренные примеры. Выполнить средствами пакета MathCAD последовательность заданий из указанного преподавателем варианта. Решения задач оформить в виде единого документа. Каждую задачу обязательно со- провождать комментариями. Решить дифференциальное уравнение первого порядка чис- ленным методом. При решении использовать параметры и условия, заданные в табл. 9. Построить график функции, являющейся решени- ем уравнения.       Таблица9 Таблица9
     Решить задачу п. 2.1 с начальными условиями и параметра- ми, указанным в задании 2.1 и начальными условиями, заданными в табл. 10. Построить графики двух решений в одной системе коор- динат. Решить задачу п. 2.1 с начальными условиями и параметра- ми, указанным в задании 2.1 и начальными условиями, заданными в табл. 10. Построить графики двух решений в одной системе коор- динат.Таблица10
 Решить систему дифференциальных уравнений первого по- рядка численным методом. При решении использовать параметры и Решить систему дифференциальных уравнений первого по- рядка численным методом. При решении использовать параметры иусловия, заданные в табл. 11. Построить график функции, являющейся решением уравнения с параметрами, позволяющими наблюдать ха- рактерные значения решения.       Таблица11 Таблица11
   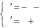 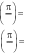 Решить дифференциальное уравнение второго порядка чис- ленным методом. При решении использовать параметры и условия, заданные в табл. 10. Построить график функции, являющейся решени- ем уравнения с параметрами, позволяющими наблюдать характерные значения решения. Решить дифференциальное уравнение второго порядка чис- ленным методом. При решении использовать параметры и условия, заданные в табл. 10. Построить график функции, являющейся решени- ем уравнения с параметрами, позволяющими наблюдать характерные значения решения.    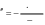 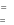 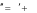 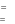   Таблица12 Таблица12
   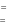 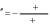  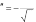 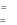  Оформите протокол лабораторной работы средствами MathCAD. Оформите протокол лабораторной работы средствами MathCAD.Содержание отчетаТитульный лист. Решение всех задач с комментариями. Контрольные вопросыДайте определение дифференциального уравнения. В чем состоит суть решения задачи Коши? Что из себя представляет решение системы дифференциаль- ных уравнений первого порядка? 81  В чем состоит отличие алгоритма решения дифференциально- го уравнения первого порядка от решения дифференциального урав- нения второго порядка? | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


