методичка. Решение математических задач в среде Mathcad методические указания к лабораторным работам
 Скачать 2.22 Mb. Скачать 2.22 Mb.
|
ЛАБОРАТОРНАЯ РАБОТА № 3ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ УРАВНЕНИЙ И СИСТЕМ УРАВНЕНИЙ В СРЕДЕ MATHCAD Цель лабораторной работы – ознакомиться с основными прие- мами решения уравнений и систем уравнений численными методами. Определение комплексных чиселРешения некоторых уравнений содержат комплексные числа. MathCAD воспринимает комплексные числа в форме a + bi, где a и b – обычные числа. Комплексные числа могут также возникать в резуль- тате вычислений, даже если все исходные значения вещественны.  Например, если вычислить 1, MathCAD возвращает i. При вводе комплексных чисел нельзя использовать i саму по себе для ввода ком- плексной единицы. Нужно всегда печатать 1i, в противном случае MathCAD истолкует i как переменную. Когда курсор покидает выра- жение, содержащее 1i, MathCAD скрывает избыточную единицу. Не- которые операции над комплексными числами показаны на рис. 13. Например, если вычислить 1, MathCAD возвращает i. При вводе комплексных чисел нельзя использовать i саму по себе для ввода ком- плексной единицы. Нужно всегда печатать 1i, в противном случае MathCAD истолкует i как переменную. Когда курсор покидает выра- жение, содержащее 1i, MathCAD скрывает избыточную единицу. Не- которые операции над комплексными числами показаны на рис. 13.  35   Определим комплекные переменные Определим комплекные переменные i z1 i z1z2 r e(i ) z1 z2 1.545 4.755i Выполним некоторые действия  z2 4.755 1.545i Re(z2) 1.545 Im(z2) 4.755 z2 4.755 1.545i Re(z2) 1.545 Im(z2) 4.755z1  z3 101.127 73.473i z3 101.127 73.473iРис. 13 Решение систем линейных уравненийДля решения систем линейных уравнений в системе MathCAD введена функция lsolve(A,B), которая возвращает вектор X для систе- мы линейных уравнений A · X = B при заданной матрице коэффици- ентов A и векторе свободных членов B. Если уравнений n, размер- ность вектора B должна быть n, а размерность матрицы A – n×n. При- мер решения системы линейных уравнений:  2x1 0, 03x1 2x1 0, 03x10, 77x1 рассмотрен на рис. 14. 0, 24x2 0, 06x3 9 0,12x3 5 РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ A*X=   B   2  A 0.03 A 0.030.77 0.24  3.3 3.30.32 0.06   0.12 0.12 0.22 0.22Задание коэффициентов систем   9  B 5 B 52  3.873 3.873Задание вектора свободных член  X lsolve( A B) X X lsolve( A B) X0.69  23.652 23.652Рис. 14 Решение системы Для простейших уравнений вида F(x) = 0 решение находится с помощью функции root(Выражение, Имя_переменной). Эта функция возвращает значение переменной, при котором вы- ражение дает 0. Функция реализует вычисления итерационным мето- дом, причем можно задать начальное значение переменной. Это осо- бенно полезно, если возможно несколько решений. Тогда выбор решения определяется выбором начального значения переменной. Первое применение этой функции позволяет найти первый корень X1. Для поиска второго корня X2 первый исключается делением F(x) на (x–X1). Соответственно, для поиска третьего корня X3 F(x) делится еще и на (x–X2). Пример использования функции приведен на рис. 15.  НАХОЖДЕНИЕ КОРНЕЙ КУБИЧЕСКОГО УРАВНЕНИЯ       a3 2 a2 5 a1 43 a0 92 Коэффициенты a3 2 a2 5 a1 43 a0 92 Коэффициенты     F( x) a3 x3 a2 x2 a1 a0 Задание полинома Вычисление действительного корня F( x) a3 x3 a2 x2 a1 a0 Задание полинома Вычисление действительного корня  x 2 x1 root( F( x) x) x1 4.018 x 2 x1 root( F( x) x) x1 4.018  Вычисление других корней Вычисление других корней       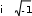 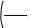  x 1 1 i x2 root F( x) x x1 x 1 1 i x2 root F( x) x x1x x2 0.759 2.35i  x3 root x3 rootF( x) x   ( x x1) ( x x2) ( x x1) ( x x2)x3 0.759 2.35i   Рис. 15 Рис. 15Для поиска корней обычного полинома p(x) степени nможно ис- пользовать функцию polyroots(V). НАХОЖДЕНИЕ КОРНЕЙ УРАВНЕНИЯ 4-ОЙ СТЕПЕНИ Она, как показано на рис. 16, возвращает вектор корней много- члена (полинома) степени n, коэффициенты которого находятся в векторе V, имеющем длину, равную n+ 1.        V0 12 V1 8 V2 33 V3 25 V4 41 V0 12 V1 8 V2 33 V3 25 V4 41   1.395 1.3950.01 0.524i polyroots ( V) 0.01 0.524i  0.764 0.764 Рис. 16 Функцию root можно использовать и в составе функции пользо- вателя, создаваемой специально для решения конкретной задачи. Например, как показано на рис. 17, с ее помощью можно организовать решение уравнения при различных значениях параметра a.  GH( a x) root ex 3 a x3 x  a 1 5 x0 0 xa GH a xa 1   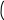      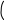    a xa a xa Рис. 17 Решение систем нелинейных уравненийПри решении систем нелинейных уравнений используется спе- циальный вычислительный блок, открываемый служебным словом – директивой Given, имеющей следующую структуру: Given Уравнения Ограничительные условия Выражения с функциями Find и Minerr Рекомендуется дополнять блок проверкой решения системы. В блоке может использоваться одна из следующих функций: Find(v1,…,vn) – возвращает значение одной или ряда перемен- ных для точного решения; Minerr(v1,…,vn) – возвращает значение одной или ряда пере- менных для приближенного решения. Между этими функциями существуют принципиальные разли- чия. Первая функция используется тогда, когда решение реально су- ществует (хотя и не является аналитическим). Вторая функция пыта- ется найти максимальное приближение даже к несуществующему решению путем минимизации среднеквадратической погрешности решения. Ограничительные условия вводятся следующими операторами:
 В решающих блоках для определения условия равенства исполь- зуется знак логического равенства =, извлекаемый из меню или вво- димый комбинацией клавиш Ctrl +. В решающих блоках для определения условия равенства исполь- зуется знак логического равенства =, извлекаемый из меню или вво- димый комбинацией клавиш Ctrl +.Функции Find и Minerr, как показано на рис. 18, могут использо- ваться для решения одного уравнения.  Рис. 18 Для нахождения начальных приближений поиска вещественных корней весьма полезно построить графики кривых, входящих в систе- му уравнений. Полученные точки пересечения можно использовать для дальнейшего поиска корней. Пример такого решения приведен на рис. 19. При использовании функции Minerr при решении систем нели- нейных уравнений нужно проявлять осторожность и обязательно предусматривать проверку решений. Полезно как можно точнее ука- зывать начальное приближение к решению. 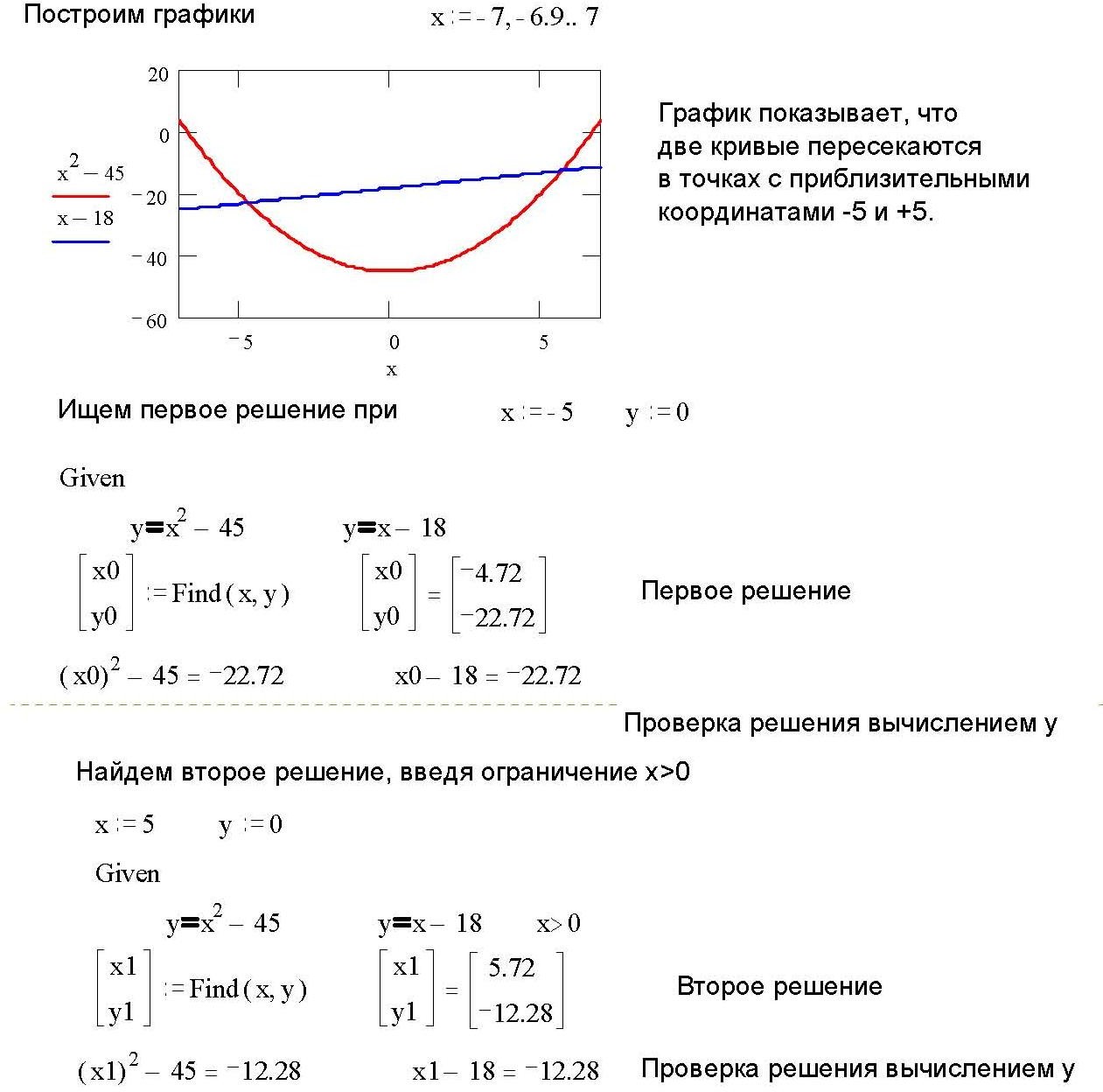 Рис. 19 Порядок выполнения работыВойти в систему MathCAD. Внимательно ознакомиться с опи- санием лабораторной работы. Выполнить некоторые рассмотренные примеры. После завершения изучения описания удалить с листа рас- смотренные примеры. Выполнить средствами пакета MathCAD последовательность заданий из указанного преподавателем варианта. Решения задач оформить в виде единого документа. Каждую задачу обязательно со- провождать комментариями. Определить все корни уравнения. 1. x+ ln(x+ 2) = 0; 2. x5 – x– 0,2 = 0; 3. x4 +2x3 – x– 1 = 0; 4. x3 – 0,2x2 – 0.2x– 1,2 = 0;  2sin2 x 2sin2 x5. 3cos2 x 0 ; 6. 5x3 +12x2 + 3x+4 = 0; 3 4 7. x2 – sin 5x= 0; 8. x4 – 4x3 + x2 – 5x+ 4 = 0; 9. 1,8x4 – sin10x= 0; 10. x3 – 2x2 + x– 3 = 0. Определить для заданного варианта все корни нелинейного уравнения с помощью функции root.  1. x3 x– 10= 0; 6. 2sin х 1. x3 x– 10= 0; 6. 2sin х3cos х 0 ; 3 4 3. x4 x2 + 5= 0; 8. 8x3 2x2 3x 2 = 0; 4. sin 2х cos 2х 0 ; 9. sin х cos х 0 ;  5. x4 + 2x3 x 1 = 0; 10. sin х 5. x4 + 2x3 x 1 = 0; 10. sin хcos х 0 . 2 3  Составить программу для решения системы линейных урав- нений, используя функцию lsolve. Значения коэффициентов Ai, Bi, Ciи свободных членов Diдля заданного варианта взять из табл. 8. Выпол- нить проверку решения: Таблица8
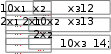 Составить программу решения системы линейных уравне- ний. Выполнить проверку решения. Составить программу решения системы линейных уравне- ний. Выполнить проверку решения.1. 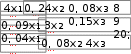 2. 2.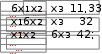 3. 3.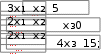 4. 4.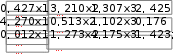 5. 5.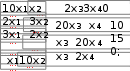 6. 6.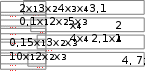 7. 7.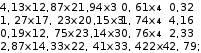  8. 8.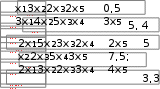 9. 9.
 10. 10. Выполнить задание для своего варианта, используя соответ- ствующий оператор решения, предварительно определив начальные приближения с помощью построения графика. Найти все корни уравнения x2 25x2  5 2x2 5 2x274 0. 49 Решить уравнение x5 1 0 . x4 8x 63 0 . 4x3 6x2 4x 1 0 . 8x4 8x3 x 190 0 . Решить уравнение (8x 7)2(4x 3)(x 1) 4,5 . Решить уравнение x2 x 8 . 2  x 1 x 1 1)(x 2)(x 3)(x 4) 1. Решить уравнение (x 4)3(x 5)3 2(x 5)3 (x 4)3 0 . Найти все корни уравнения x3 2x 5 3 1.  Найти все решения для системы уравнений предварительно определив начальные приближения с помощью построения графиков: Найти все решения для системы уравнений предварительно определив начальные приближения с помощью построения графиков: 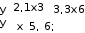  1. 6. 1. 6.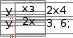 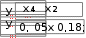 2. 7. 2. 7.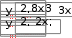 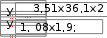 3. 8. 3. 8.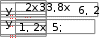 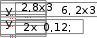 4. 9. 4. 9.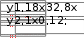 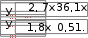 5. 10. 5. 10.Составить для заданного варианта программу для решения системы нелинейных уравнений, используя функцию findили minner. 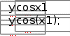 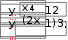 1. 1.6. 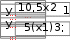 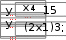 2. 7. 2. 7. 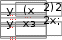 3. 8. 3. 8.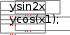 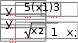 4. 9. 4. 9.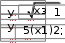 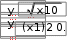 5. 10. 5. 10.Оформите протокол лабораторной работы средствами MathCAD. |

