Преподаватель - Боткин А.В. Преподаватель - Боткин А. Решение организационных вопросов, вопросов техники безопасности, расчет ожидаемого экономического эффекта
 Скачать 3.24 Mb.
|
Рис.2При расчете конкретного этапа нагружения принимается гипотеза, согласно которой при  считается, что  , а элемент для которого выполняется условие  считается находящимся в упругом состоянии.Алгоритм линеаризации задачи пластичности рассмотрим, мысленно проследив за одним конечным элементом. Пусть для нашего элемента на каком то шаге нагружения в первом приближении (для всех элементов ) рассчитано НДС- точка с координатами ( ) см. рис.2, причем условие  не выполняется. Тогда формирование матрицы жесткости системы уравнений необходимо осуществлять с уточнённой для этого элемента матрицей упругопластичности.В матрице уточняется коэффициент вязкости: 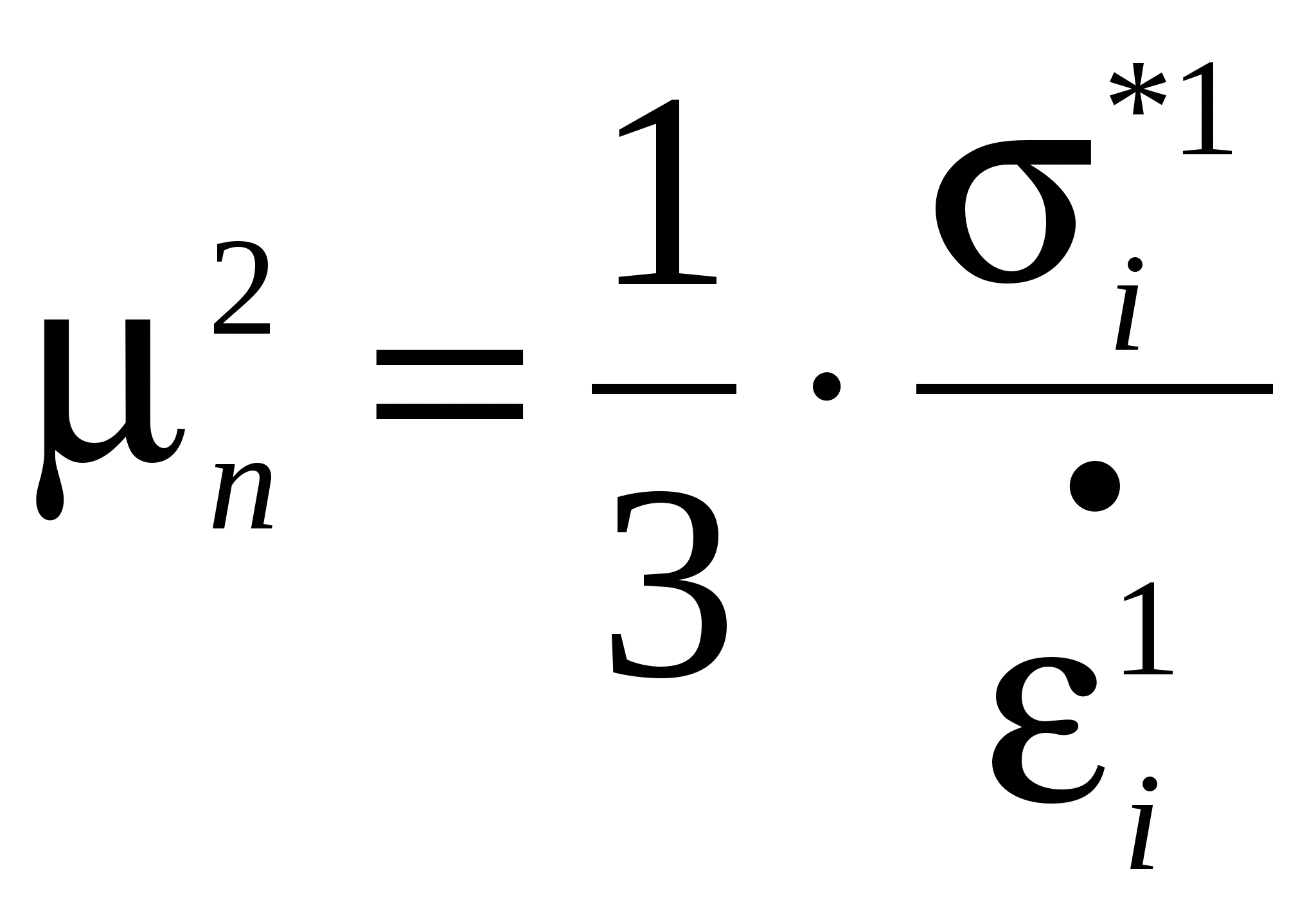 . Далее система МКЭ решается второй раз, т.е. выполняется 2-е приближение и т.д. пока не удовлетворится условие (8) для всех конечных элементов.При формировании вектора нагрузки {F} перед каждым этапом нагружения учитывают гидростатическое давление:  ,где, Fi –добавочная сила в i-ом узле гидростатического давления в окружающих узел элементах, L- число окружающих i-ый узел элементов. При уточнении  по элементам остается неизменным, рассчитанным по результатам предыдущим этапов нагружения модели: ,где,  - гидростатическое давление в элементе накопленное к р-ому этапу нагружения, -объемная степень деформации элемента и интервал времени для j-го этапа нагружения модели. Т.е. добавочная сила в i-ом узле от приближения к приближению не уточняется.Временной интервал на каждом шаге нагружения должен удовлетворять неравенству:  .Отметим, что при моделировании горячего формоизменения заготовки и решении задачи в приращениях перемещений, линеаризация осуществляется с использованием упругих методов: метод переменных параметров упругоооооо; метод касательных жесткостей; метод дополнительных деформаций, т.е. как и при решении задач холодного деформирования. При решении задачи в скоростях течения, с пропорциональностью девиатора напряжений девиатору скоростей деформации и сжимаемой по закону Гука скоростное упрочнение металла учитывается использованием в расчетной программе диаграммы скоростного упрочнения  .Диаграмма представляется, как правило в виде функциональных зависимостей:  ,где,  - параметры также указываются в программе; -линейный модуль скоростного упрочнения металла.Зависимость (9) (уравнение линии) получают обработкой экспериментальных данных, полученных при испытании металлических образцов. При решении задачи в приращениях перемещений используется диаграмма деформирования  , как и при моделировании холодного деформирования. Отличие состоит в том, что диаграмма должна соответствовать температуре обработки и средней скорости деформации заготовки.Перед каждым этапом нагружения уточняются: координаты, матрицы дифференцирования, жесткости элементов.   и т.д. – абцисса j-го узла,  - скорость перемещения j-го узла в направлении оси OX.Как уже отмечалось выше учитывается накопленное гидростатическое давление, но коэффициент вязкости для всех элементов в первом приближении, (при первом решении системы) на каждом очередном этапе нагружения модели приравниваются  .  |