Преподаватель - Боткин А.В. Преподаватель - Боткин А. Решение организационных вопросов, вопросов техники безопасности, расчет ожидаемого экономического эффекта
 Скачать 3.24 Mb. Скачать 3.24 Mb.
|
ВведениеЦель изучения дисциплины, место дисциплины в учебном процессе, структура дисциплины, распределение по часам, лекции, лабораторные работы, практика, вид отчетности (по рабочей программе). Современный процесс ОМД это процесс обеспечивающий получение заготовки детали максимально приближенной по форме и размерам к детали, с заданным уровнем свойств, при минимальных затратах материалов, энергии, времени, труда. Процесс, обеспечивающий безопасность труда и не нарушающий экологию окружающей среды. Обычно алгоритм разработки технологии включает следующие этапы:
Выполнение перечисленных выше этапов обеспечивает разработку технологического процесса, удовлетворяющего требованиям, предъявляемым к современной технологии, причем некоторые основные этапы (например-5,6,7) невыполнимы без использования математических моделей, современных вычислительных машин и применения обширных знаний теории и практики ОМД. Понятие математической моделиМатематической моделью пластического формоизменения заготовки называют его приближенное математическое описание, позволяющее найти в области пластического течения распределение скоростей деформаций, температур, напряжений, рассчитать вероятность разрушения металла в любом локальном объеме металла, конфигурацию заготовки в любой момент времени и определить оптимальные условия деформирования заготовки. Под математическим описанием процесса понимают: уравнения, условия, неравенства, алгоритмы и программы для ЭВМ, позволяющие моделировать формоизменение заготовки. Оптимальные условия деформации это: температура, скорость деформирования, размеры и форма заготовки, положение заготовки и т. д., при которых возможно деформирование заготовки без разрушения металла; условия, при которых обеспечивается заданный эксплуатационными требованиями уровень механических свойств заготовки, ее форма и размеры, соответствующие чертежу поковки; условия, при которых имеют место минимальные затраты тепловой и механической энергии; условия, при которых происходит макроскопически качественное формоизменение заготовки – отсутствие зажимов, складок, прострелов, возможных вследствие неправильного течения металла в полости штампа, что обусловлено формой исходной заготовки и ее укладкой, конструкцией штампа и т. д.; условия, обеспечивающие удовлетворительную стойкость штамповой оснастки; условия, обеспечивающие максимально возможную производительность. Математическое моделирование процессов ОМД является частью дисциплины- теория обработки металлов давлением, предусмотренной Государственным образовательным стандартом. Согласно, учебного плана специальности 120400, ТОМД изучается студентами в 5,6,7 семестрах. В пятом – основы физики и механики пластической деформации. В шестом – инженерные методы расчета и основы теории операций ОМД. В седьмом изучается один из современных исследовательских методов моделирования формоизменения заготовки в операции ОМД- метод конечных элементов. Цель изучения дисциплины в седьмом семестре заключается в формировании знаний основ метода конечных элементов (МКЭ). МКЭ отличается от инженерных методов большими возможностями по расчету локальных характеристик Н.Д.С. заготовок и универсальностью. Метод не имеет ограничений, обусловленных размерностью задачи пластичности, формой заготовки, формой инструмента (штампа). Метод позволяет учесть при решении задач многие факторы и параметры процесса формоизменения заготовки в операции: температуру; скорость деформирования; условия трения; неоднородность свойств металла. Метод позволяет обнаружить на модели образование таких дефектов как: складки; зажимы; прострелы. Результаты расчета Н.Д.С. заготовки методом МКЭ позволяют использовать различные модели разрушения металла при деформации, с учетом истории деформации отдельной частицы заготовки. Применение метода МКЭ позволяет на качественно ином уровне принимать проектировочные научно-обоснованные технические решения при разработке технологических процессов ОМД и тем самым уменьшать время опытной доработки этих процессов. Сущность метода конечных элементовСущность МКЭ заключается в следующем. Нагружаемое тело представляется составленным из элементов конечных размеров. Количество этих элементов конечно. Каждый элемент, называемый конечным, задается в пространстве координатами вершин узлов. Иначе говоря, сплошное тело геометрически представляется в пространстве координатами некоторых его материальных точек являющихся вершинами конечных элементов. Представление тела, как совокупности узлов, делается для того, чтобы в дальнейшем рассчитать перемещения узлов вдоль осей координат (приращения перемещений или скорости течения узлов) путем решения, как правило, линейной системы уравнений равновесия всех узлов. Левая часть каждого уравнения представляет собой сумму внутренних сил действующих на узел со стороны всех окружающих узел конечных элементов. Правая часть каждого уравнения равна нулю, если узел внутренний или равна внешней нагружающей силе, если внешний узел испытывает нагружение. С математической точки зрения непрерывная функция перемещений (приращений перемещений или скоростей течения узлов) материальных точек составляющих тело и определенная в пространственной области занимаемой на данный момент им заменяется путем конечно элементного представления совокупностью конечно-непрерывных функций перемещений. Каждая из этих функций определена на своем конечном элементе. При этом каждая конечно-непрерывная функция перемещений (приращений перемещений или скоростей течения узлов) формально представляется (записывается) через значения перемещений узлов составляющих конкретный элемент: например для треугольного конечного элемента Ux,n=Nx,iUx,i+ Nx,jUx,j +Nx,mUx,m=1x+2y+3; (1) где, Ux,n – кусочно-непрерывная функция описывающая перемещения материальных точек входящих в n-ый конечный элемент, Ux,i, Ux,j, Ux,m – значения перемещений узлов в направлении оси ОХ соответственно для i, j, m узлов, Nx,i, Nx,j, Nx,m – так называемые функции формы содержат аргументы функции (X и Y) в той же степени что и полином (1) принятый для описания перемещений внутри К.Э. Кусочно-непрерывные функции соответствующих элементов (имеющих общую сторону или грань) удовлетворяют равенствам вида: U(n)x,i = U(k)x,i, где n и k номера соприкасающихся в I-ом узле элементов. Выражение элементных кусочно-непрерывных функций перемещений через значения перемещений узлов элемента позволяет выразить энергию деформации каждого элемента и внутренние силы, действующие со стороны элемента на каждый его узел через эти перемещения. Складывая эти внутренние силы, действующие на узел со стороны окружающих элементов с внешними силами, получают уравнение равновесия узла. Проделав эту процедуру для всех узлов, получают упомянутую выше систему линейных уравнений относительно значений перемещений (приращений перемещений или скоростей течения) узлов. Систему уравнений равновесия называют основной системой МКЭ. Система решается относительно узловых значений перемещений, или узловых скоростей течения, в зависимости от того, какая из теорий пластичности применяется. Если применяется деформационная теория пластичности, то после расчета узловых перемещений рассчитываются компоненты деформации и новые координаты узлов: {}n=[B]n{U}n , где {}n – матрица столбец компонент деформации x,y,xу, [B]n – матрица дифференцирования, получаемая из геометрических соотношений между перемещениями и деформациями, ее компоненты одинаковы для всех материальных точек элемента в случае линейного полинома, [U]n – матрица столбец значений перемещений узлов конечного элемента, например, для треугольного конечного элемента (см. рис 1.),           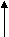 i m j Рис. 1. Перемещения узлов треугольного конечного элемента. x Заметим, что для линейного полинома (1), значения деформаций для всех материальных точек одного и того же n-го элемента одинаковы. x Компоненты напряжений рассчитываются после расчета деформаций{}n=[D]n{}n,{}n– матрица столбец компонент напряжений x,y,xy (плоское деформированное состояние) [D]n– матрица упругости или матрица упруго пластичности, зависит от того, в каком состоянии находится конечный элемент. Компоненты матрицы [D] также одинаковы для всех материальных точек конечного элемента вне зависимости от вида полинома (см. (1) правая часть) и при допущении однородности металла. Вывод основной системы МКЭ.
3. Вывод основной системы МКЭ и минимизация энергии деформации. Разбиение области на элементы сводится к заданию числа, размеров и формы непересекающихся подобластей – конечных элементов. Каждому конечному элементу соответствует группа узлов (вершин многоугольника для плоского конечного элемента, вершин многогранника для объемного конечного элемента). Всем узлам и элементам присваиваются порядковые номера. Для каждого узла указываются координаты. Вся эта информация обычно представляется в форме двух информационных файлов: файл координат и файл номеров узлов составляющих элементы. В зависимости от размерности задачи плоскую или объемную область разбивают на: одномерные элементы; двухмерные элементы или трехмерные элементы. Элементы, сторонами которых являются прямолинейные отрезки или гранями которых являются многоугольники, называют симплекс-элементами. В симплекс-элементе число узлов (вершин) всегда на единицу превышает размерность задачи. При решении одномерной задачи применяют:
При решении двухмерных задач (плоское деформированное состояние, плоское напряженное состояние) применяют:
При решении трехмерных задач применяют:
При решении осесимметричных задач, применяют кольцевые конечные элементы, например с треугольным поперечным сечением. При дискретизации области, необходимо стремиться к тому, чтобы отрезки, треугольники, тетраэдры приближались по форме к равным отрезкам, к равносторонним треугольникам, к правильным тетраэдрам. Такое разбиение обеспечивает более точные результаты, хорошо согласующиеся с экспериментальными данными. В заключении отметим, что в областях резкого изменения (большого градиента) искомой характеристики Н.Д.С. следует проводить разбиение на мелкие по размерам элементы. Каждой форме конечного элемента (отрезку, треугольнику и т.д.) соответствует (в смысле возможности определения коэффициентов полинома) интерполяционный полином, описывающий кусочно-непрерывную функцию перемещений (или приращений перемещений, или скоростей течения в зависимости от использующейся теории пластичности) внутри конечного элемента, т.е. полином с областью определения, ограниченной конечным элементом. Полиномы соответствующие симплекс-элементам содержат константы и линейные члены, члены, содержащие независимые переменные x и y в первой степени. Полином, соответствующий одномерному элементу имеет вид: Ux,n=α1+α2·x, двумерному треугольному симплекс-элементу: Ux,n=α1+α2·x+α3·y; (1) Uy,n=β1+β2·x+β3·y. Количество коэффициентов в каждом полиноме равно количеству узлов конечного элемента. Трёхмерному симплекс-элементу (тетраэдру): Ux,n=α1+α2·x+α3·y+α4·z; Uy,n=β1+β2·x+β3·y+β4·z; Uz,n=c1+c2·x+c3·y+c4·z. Методику вывода функций форм и матриц дифференцирования рассмотрим на примере треугольного конечного элемента. Напомним, что функции формы, с применением которых удаётся выразить полиномы – кусочно-непрерывные функции (1) через узловые перемещения элемента: (будем говорить далее о перемещениях узлов, но всё остаётся в силе для приращений перемещений или скоростей узлов) содержатся в выражениях: Ux,n=Nx,iqx,i+Nx,jqx,j+Nx,mqx,m; Uy,n=Ny,iqy,i+Ny,jqy,j+Ny,mqy,m. или в матричной форме: {U}n=[N]n·{q}n (2), где {U}n= 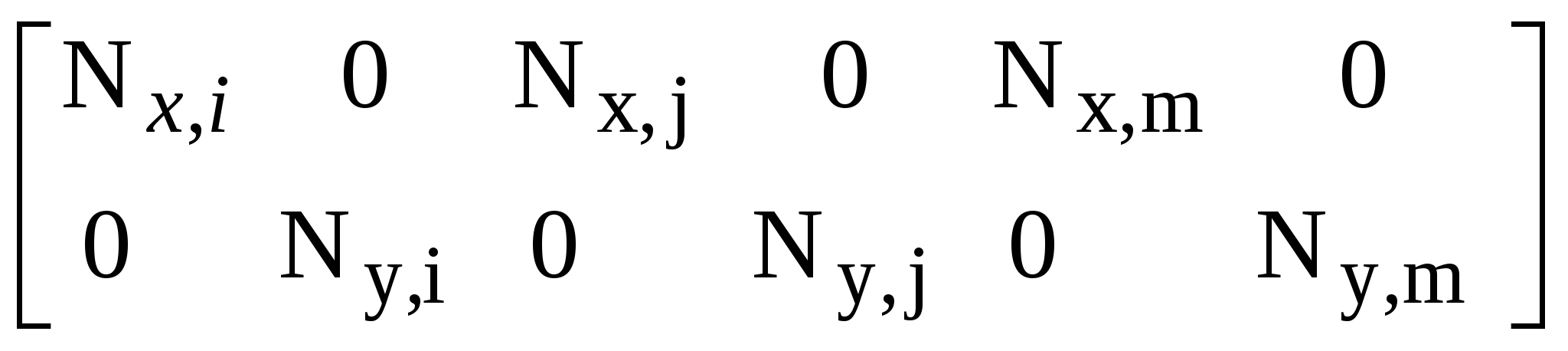 ; ;{q}n= 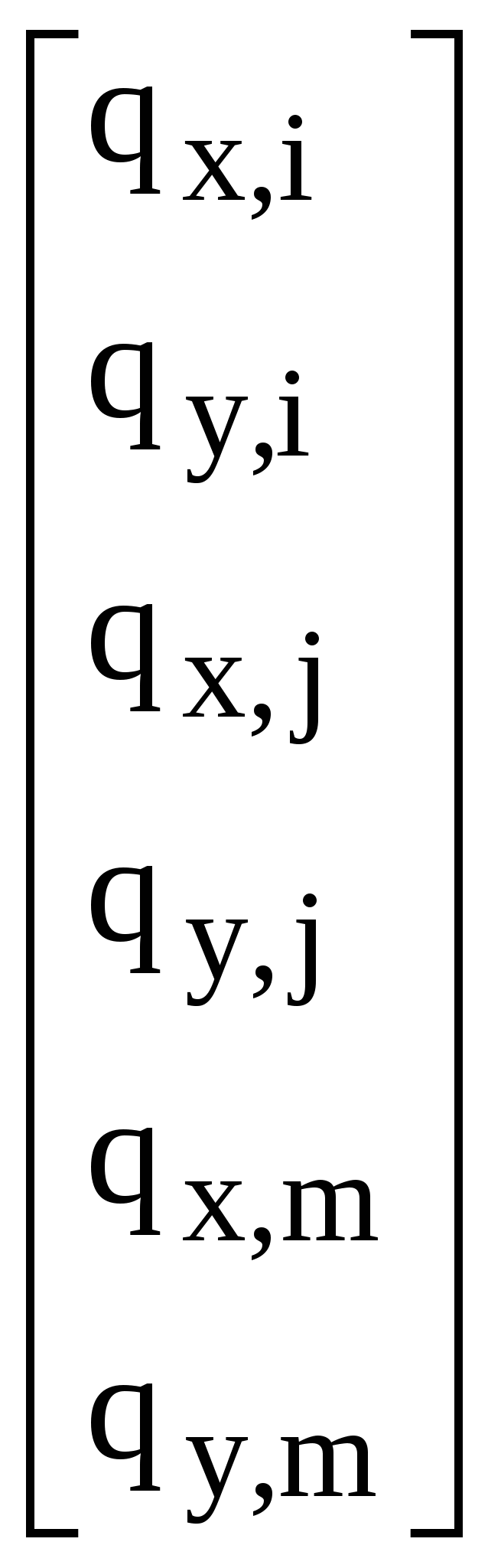 (см. рис.1.); (см. рис.1.);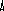  Y    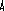 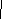 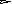  q y , m q x , m m    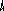  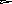  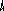  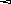  q q y , i q y , j q x , j j i n . 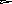  x , i X Рис.1. {U}n – матрица-столбец полиномов n-го элемента, [N]n – матрица функций форм, {q}n – матрица-столбец перемещений узлов n-го элемента. В зависимости (1) подставим значения перемещений в узлах и координаты узлов n-го элемента, получим в результате: 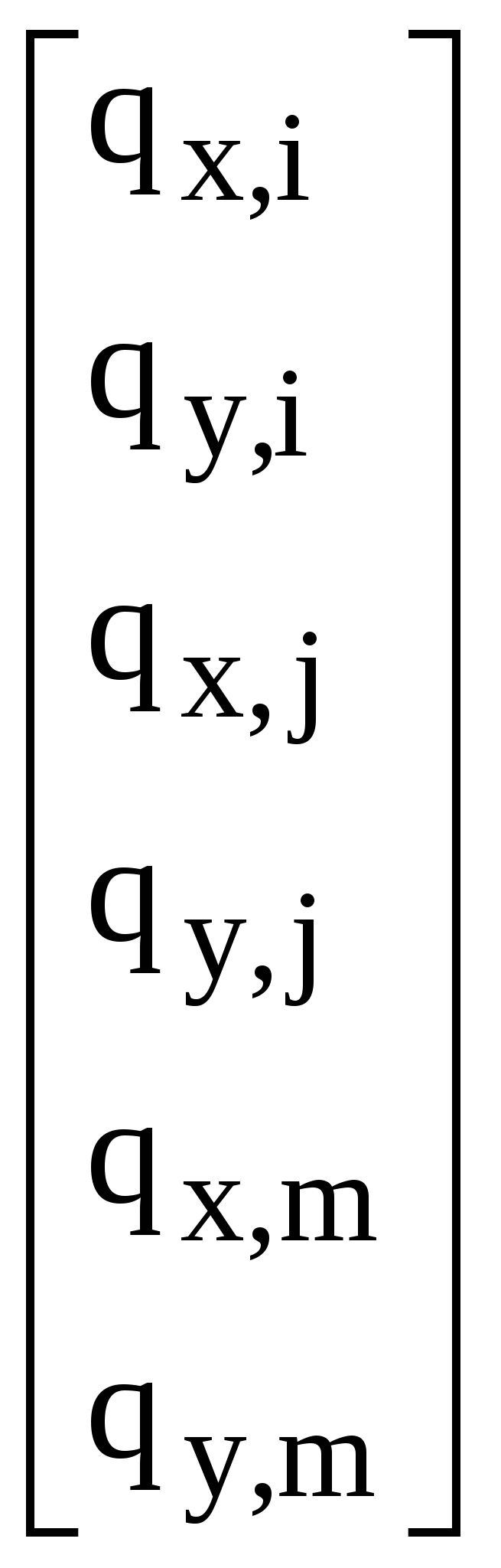 = = 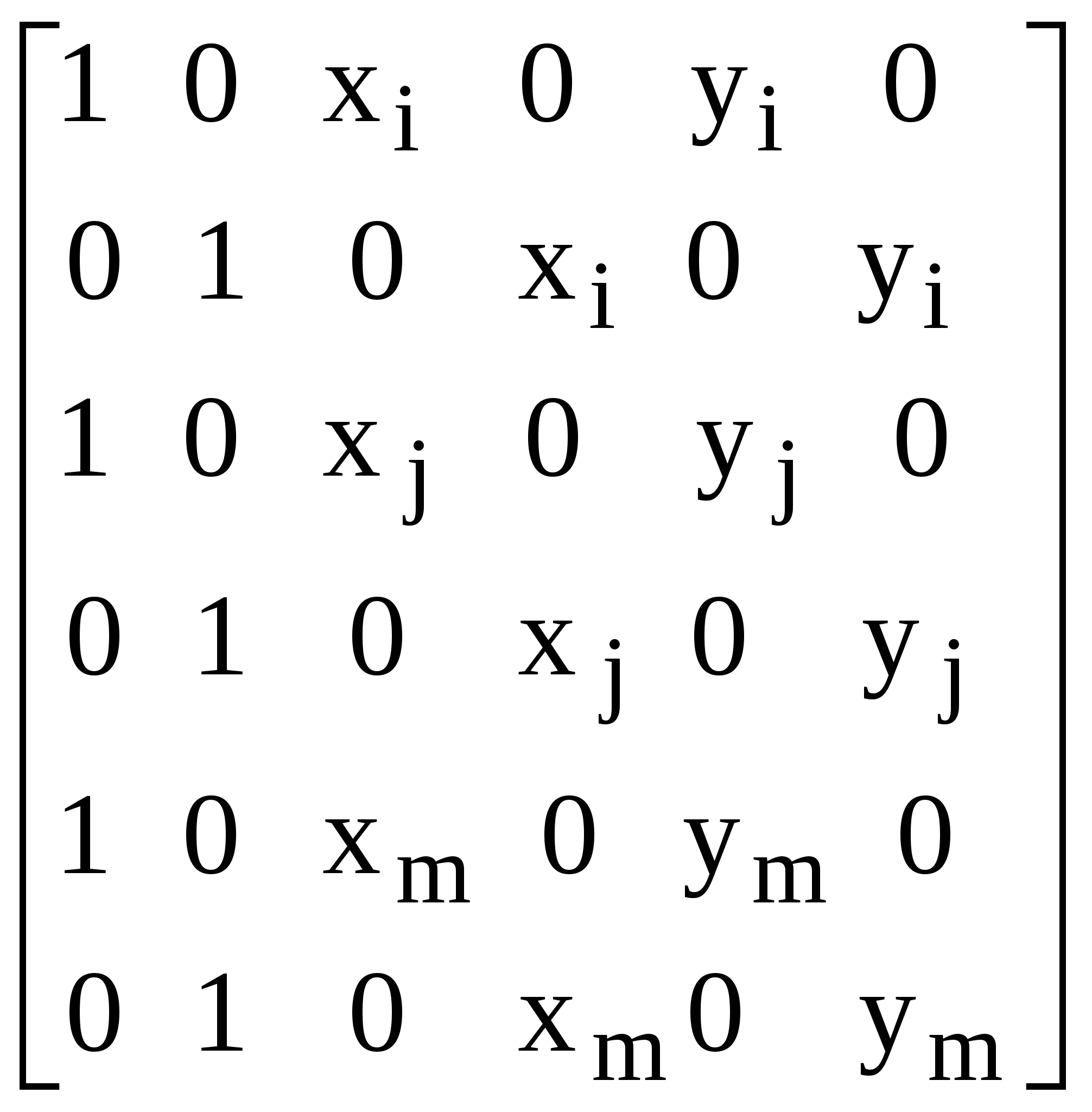 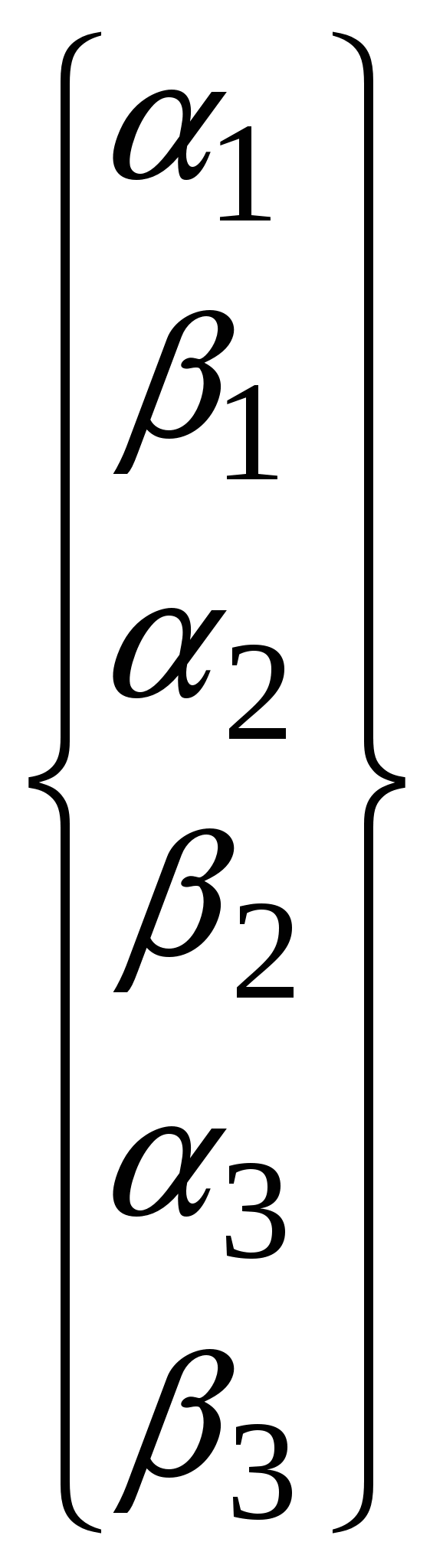 ; ;обозначим матрицу с размерами 6×6 -[c]n, а матрицу-столбец коэффициентов- {α}n, тогда: {q}n=[c]n·{α}n (3). Из математики известно, что произведение матрицы на обратную матрицу к ней, равно единичной матрице: [с]n-1[с]n=[1]. Поэтому если левую и правую части (3) умножить слева на [с]-1 то получим: {α}n=[c]-1n·{q}n (3) Зависимость (1) представим в виде: {U}n=[p]·{α}n (4); где [p]= 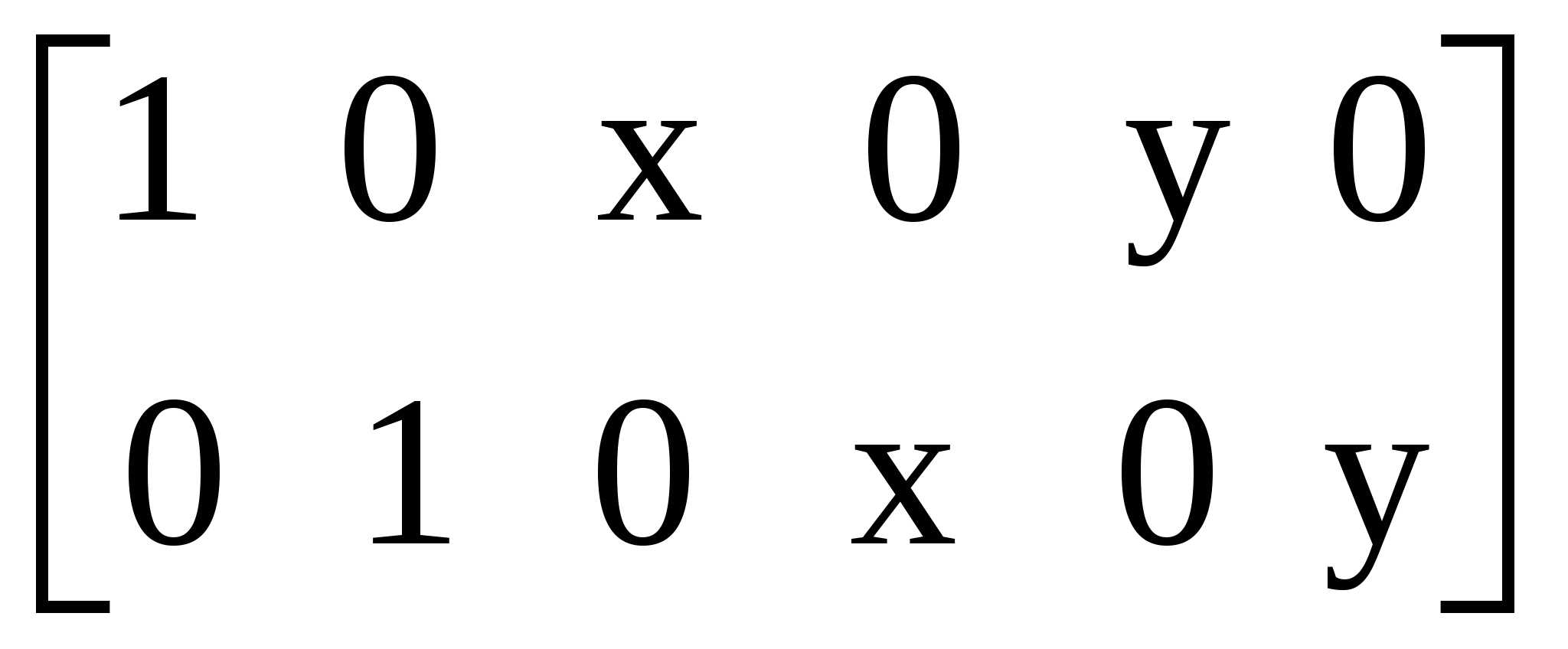 - матрица, произведение которой на {α}n равно исходным полиномам, принятым для описания кусочно-непрерывной функции с областью определения ограниченной конечным элементом. - матрица, произведение которой на {α}n равно исходным полиномам, принятым для описания кусочно-непрерывной функции с областью определения ограниченной конечным элементом.Выражение (4) с учётом (3) принимает вид: {U}n=[p]·[с]-1n·{q}n (5) Сравнивая (2) с (5) заключаем что: [N]n=[p]·[с]-1n (6) Обратная матрица [с]-1рассчитывается следующим образом: [с]-1n= 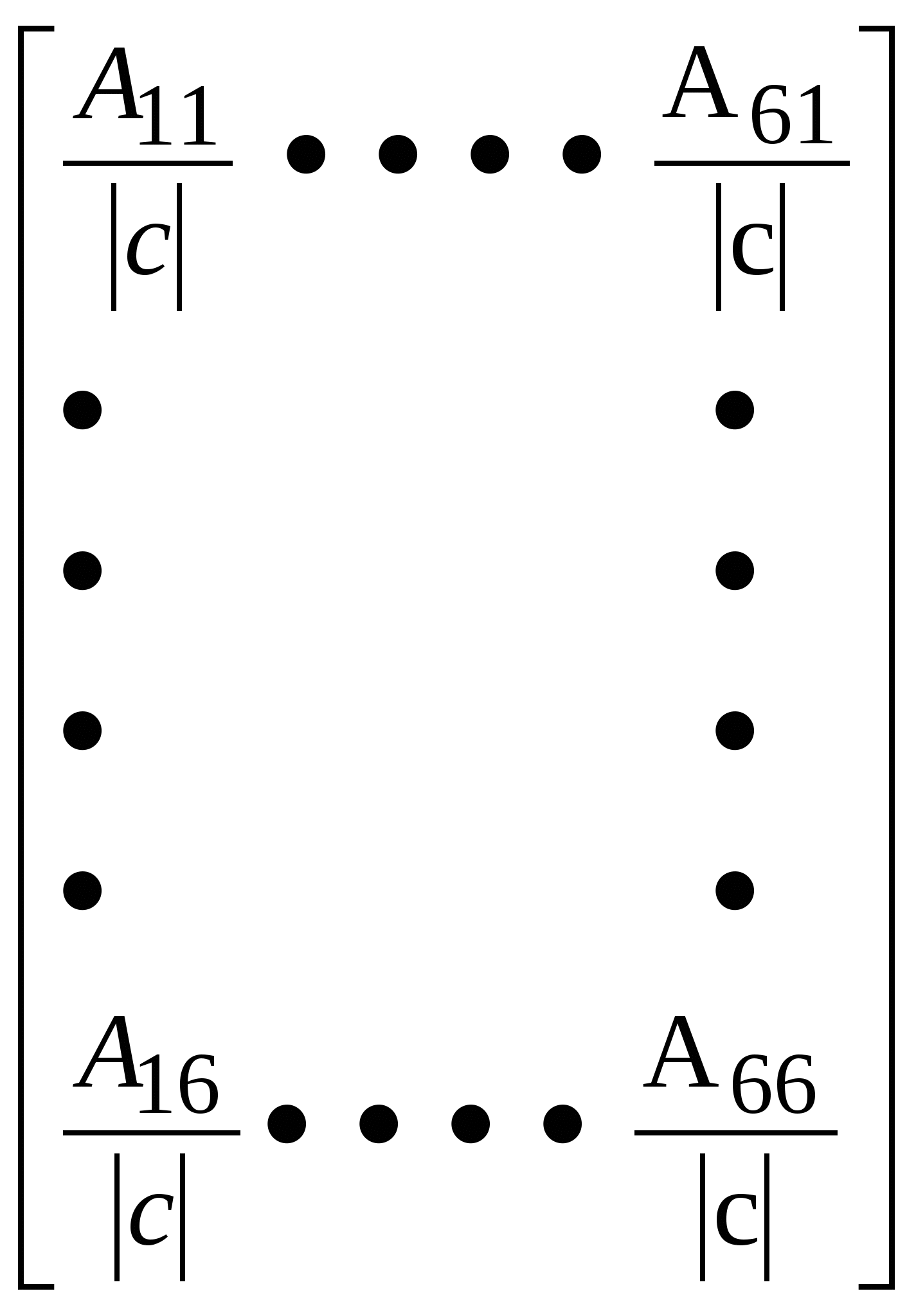 ; ;где Аi,j – алгебраическое дополнение элемента сi,j; |с| – определитель матрицы. Алгебраическим дополнением элемента сi,j называют определитель, составленный из элементов матрицы [c]n оставшихся после вычеркивания в матрице i-ой строки и j-го столбца. При этом знак перед определителем +, если i=j, и – если i<>j. Расчет по формуле (6) показывает что: Nx,i =1/(2·Δn ) ·[(xjym–xmyj)+(yj–ym)·x+(xm–xj)·y]; Nx,j =1/(2·Δn )· [(xmyi–xiym)+(ym–yi)·x+(xi–xm)·y]; Nx,m =1/(2·Δn )· [(xiyj–xjyi)+(yi–yj)·x+(xj– xi)·y]. Ny,i=Nx,i; Ny,j=Nx,j; Ny,m=Nx,m; Δn=1/2·  – площадь n-го элемента. – площадь n-го элемента.Компоненты матрицы дифференцирования [В]n получаются дифференцированием кусочно-непрерывных функций записанных в виде (2). Дифференцирование производится в соответствии с геометрическими соотношениями ( [В]n= 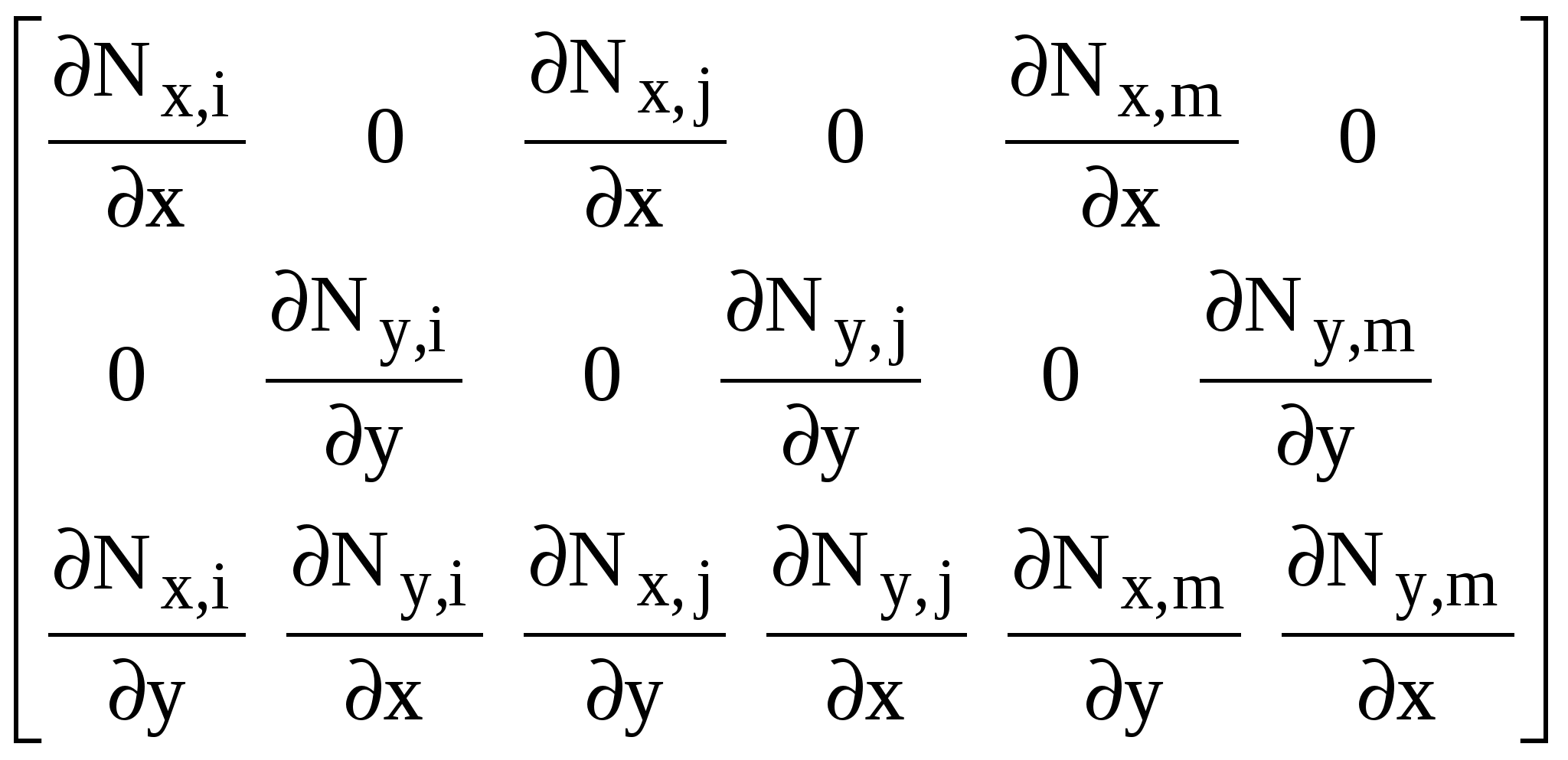 ; ;или если воспользоваться зависимостями (6): [В]n=1/(2·Δn)· 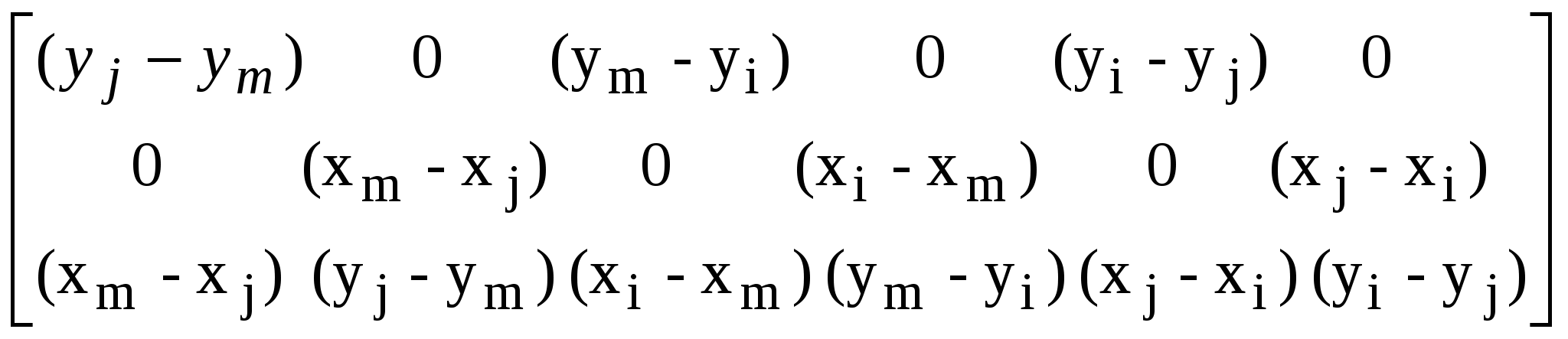 – матрица дифференцирования для треугольного конечного элемента с узлами i,j,m. – матрица дифференцирования для треугольного конечного элемента с узлами i,j,m.Для вывода основной системы МКЭ [k]·{q}={F} используется принцип минимума энергии деформации. Согласно методу баланса работ: Апл.д.=Авн; (7) где Апл.д. – работа или энергия пластической деформации; Авн – работа внешних сил. Составим из (7) энергетический функционал и выясним, при каких перемещениях узлов конечных элементов этот функционал принимает наименьшее значение. Функционал: Ф= Апл.д.–Авн (8) Апл.д.= 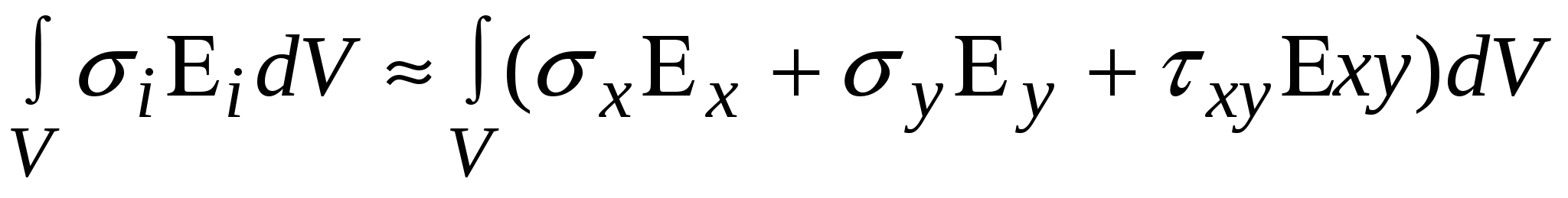 ; (9) ; (9)Выражение (9) записано для случая плоского деформированного состояния заготовки с объемом очага пластической деформации V. При конечно-элементном представлении тела интеграл (9) можно вычислить иначе: Апл.д.= или где k количество конечных элементов. С учётом зависимостей, по которым в рамках МКЭ рассчитываются {Е}i и {σ}i (компоненты деформаций и напряжений элемента) получаем: где k – количество конечных элементов; где m – количество граничных нагружаемых узлов; qj – перемещение j-го узла; Fj – сила действующая на j-й узел. Подставляя (10) и (11) в (8) получаем Из курса математики известно, что для отыскания минимального значения функционала берут производную или производные по переменным, от которых зависит функционал (Ф), приравнивают их 0, с последующим решением полученных уравнений относительно переменных. После расчёта переменных (корней системы) можно рассчитать минимальное значение Ф. Переменными в функционале (12) являются перемещения (или приращения перемещений) всех узлов. Поэтому для расчета перемещений узлов возьмём частные производные по перемещениям всех узлов, приравняем их 0 и решим полученную систему относительно их. Заметим, что каждая производная будет зависеть от перемещений узлов, т. к. в выражении (10) энергия элемента выражается через произведение матриц {q}Ti и {q}i, каждое уравнение будет иметь вид: или где [k]i=[B]T·[D]i·[B]I·Vi - матрица жёсткости i-го конечного элемента, одного из l элементов соприкасающимся в j–ом узле, Уравнение равновесия j-го узла вида (13) можно записать в виде произведения матрицы-строки коэффициентов и матрицы-столбца перемещений соответствующим не отдельным [k](2·j-1),m·{q}={F}2·j-1, для случая, если уравнение равновесия составлено для сил направленных вдоль ОХ, [k]2j,m·{q}={F}2j – для сил направленных вдоль оси OY, переменная m (если решается плоская задача) удовлетворяет неравенству: 1<=m<=(2·z), z-количество узлов, {q}=  {F}2j-1 и {F}2j – компоненты матрицы-столбца нагрузки в (2j-1)-ой и (2j)-ой строках. Ненулевые компоненты строк ( [k](2·j-1),m [k]2j,m ) рассчитываются путём сложения соответствующих компонент матриц жёсткости [k]i=[B]T·[D]i·[B]I·Vi элементов, окружающих j-ый узел. Формирование матрицы жесткости ([к ] ) – матрицы коэффициентов системы уравнений [K]*{Q}={F}. 1.Формирование матрицы жесткости способом объединения по узлам. 2. Формирование матрицы жесткости способом объединения по элементам. Каждое уравнение системы [K]*{q}={F} является уравнением равновесия (без учета инерционных сил) соответствующего узла в направлении оси OX, OY или OZ. В каждом уравнении, в левой части, сумма проекций всех внутренних сил, действующих на узел в направлении оси OX или OY или OZ. Внутренние силы действуют на узел со стороны соседствующих в узле элементов (см. рис 1). 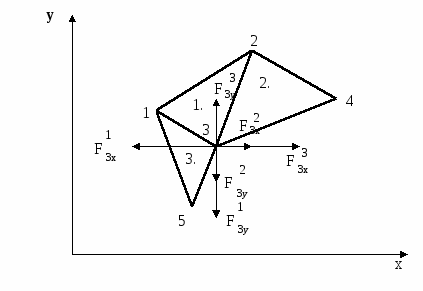 Рис. 1. 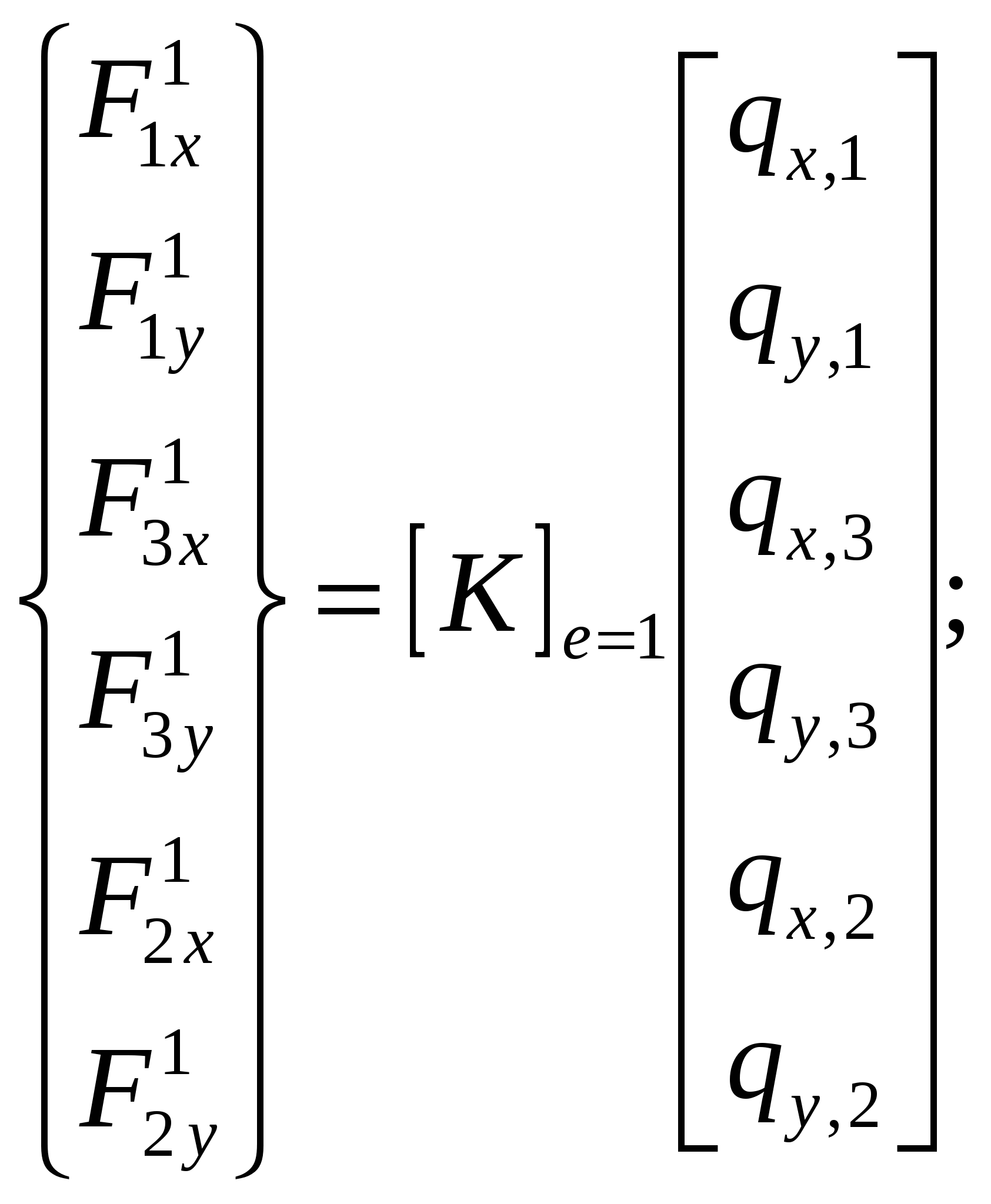 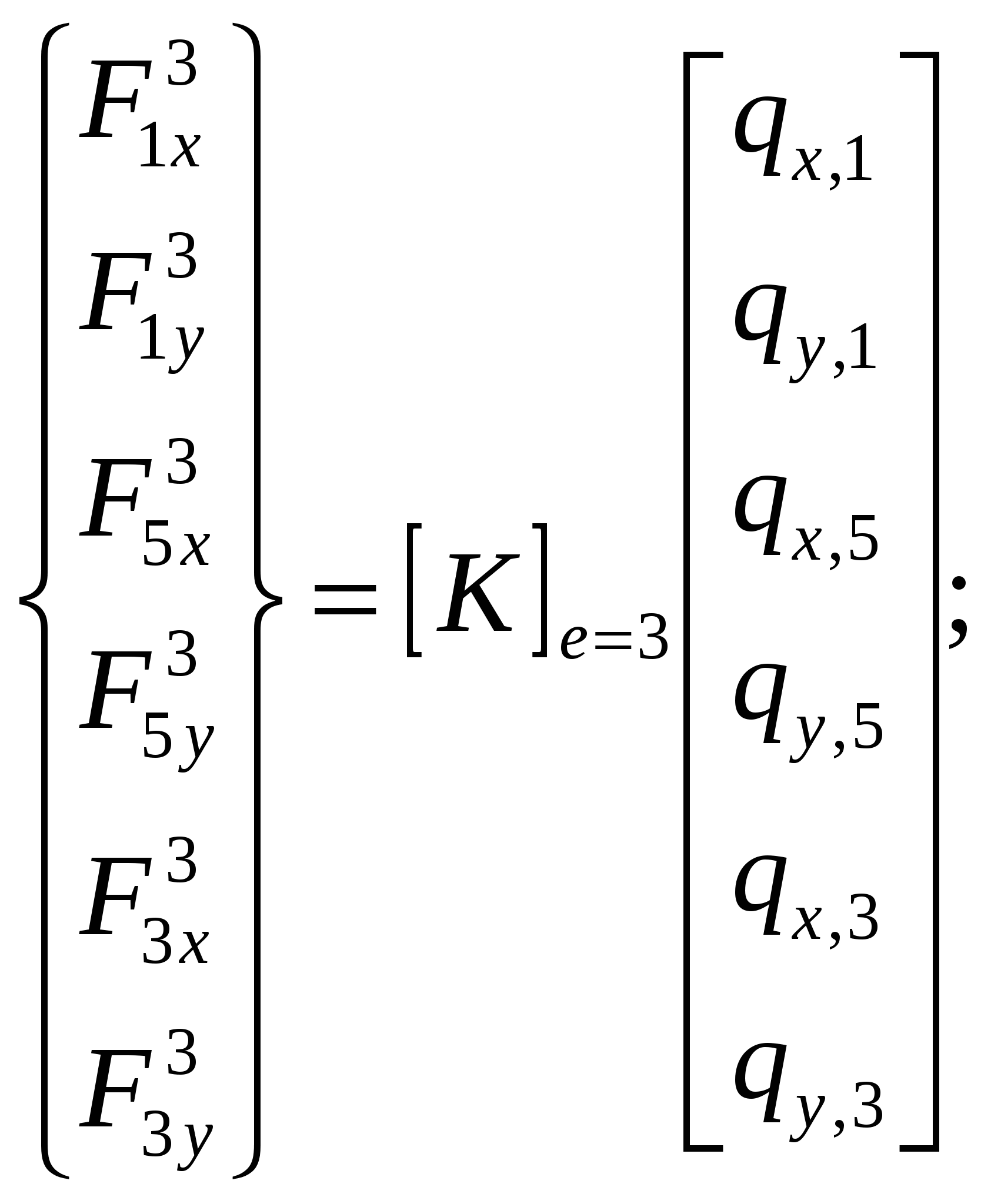 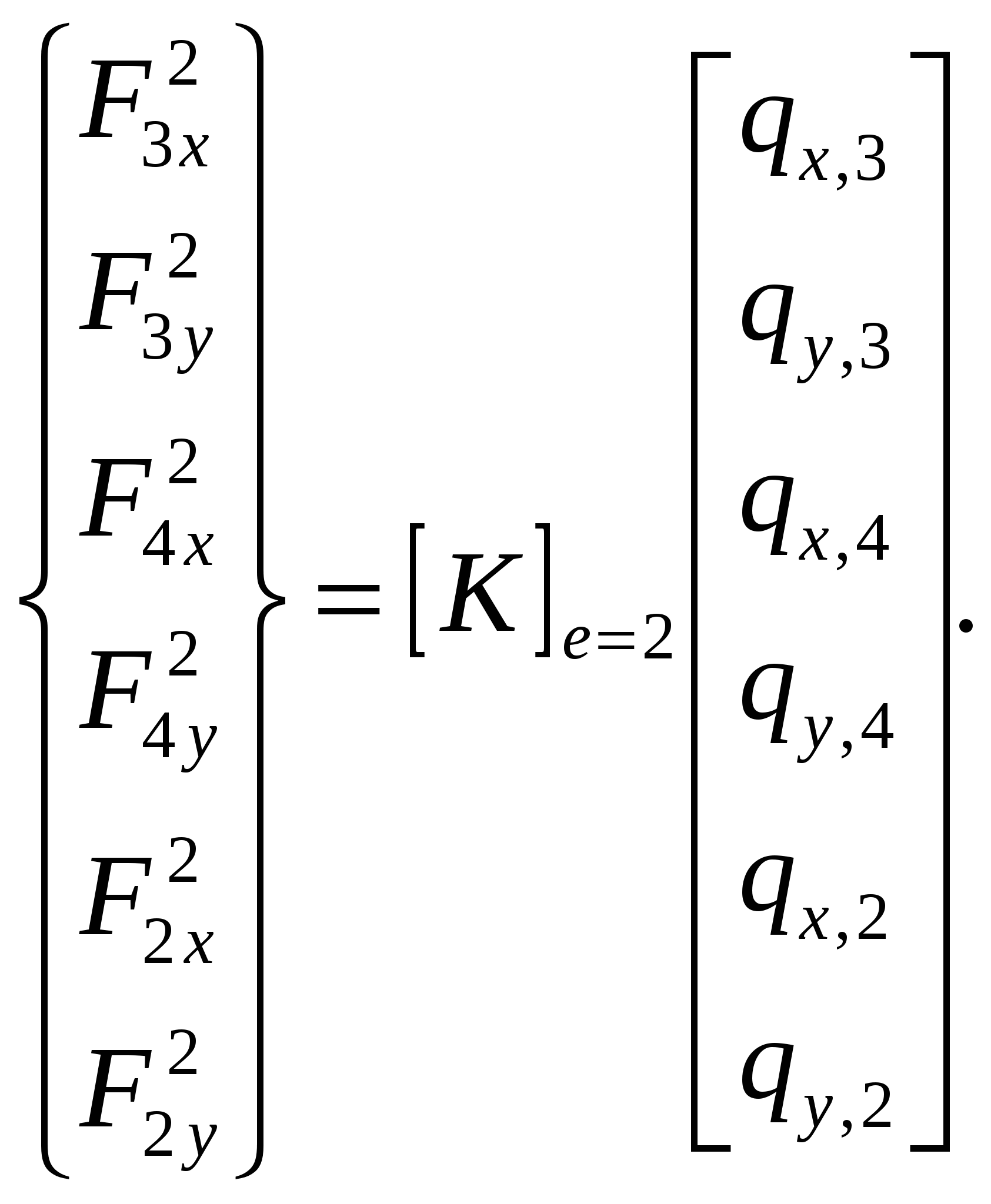 Внутренние силы выражаются через неизвестные узловые перемещения: Внутренние силы выражаются через неизвестные узловые перемещения:где [К]е=1… - матрицы жесткости элементов с номерами 1, 2, 3; Пусть: 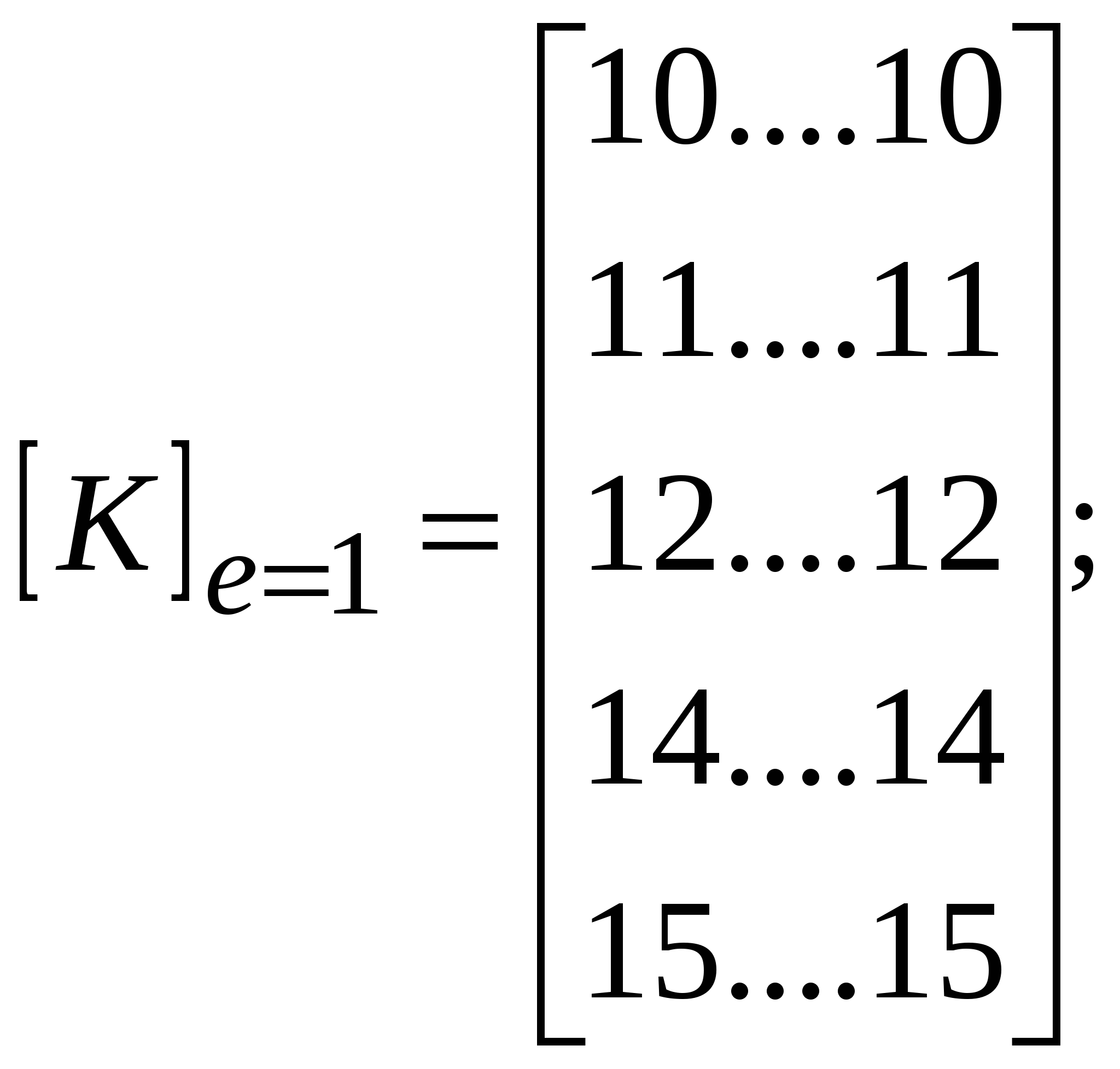 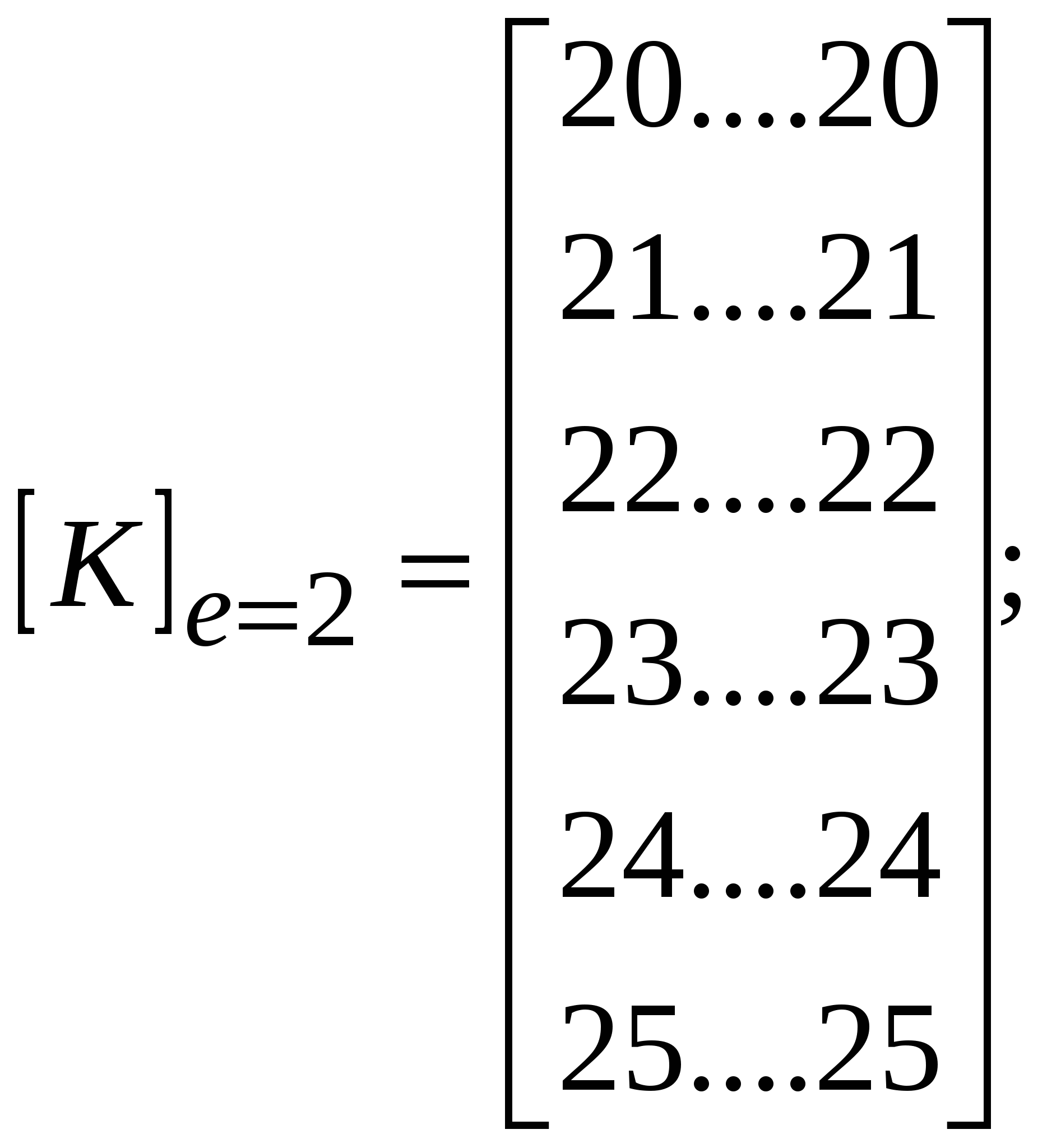 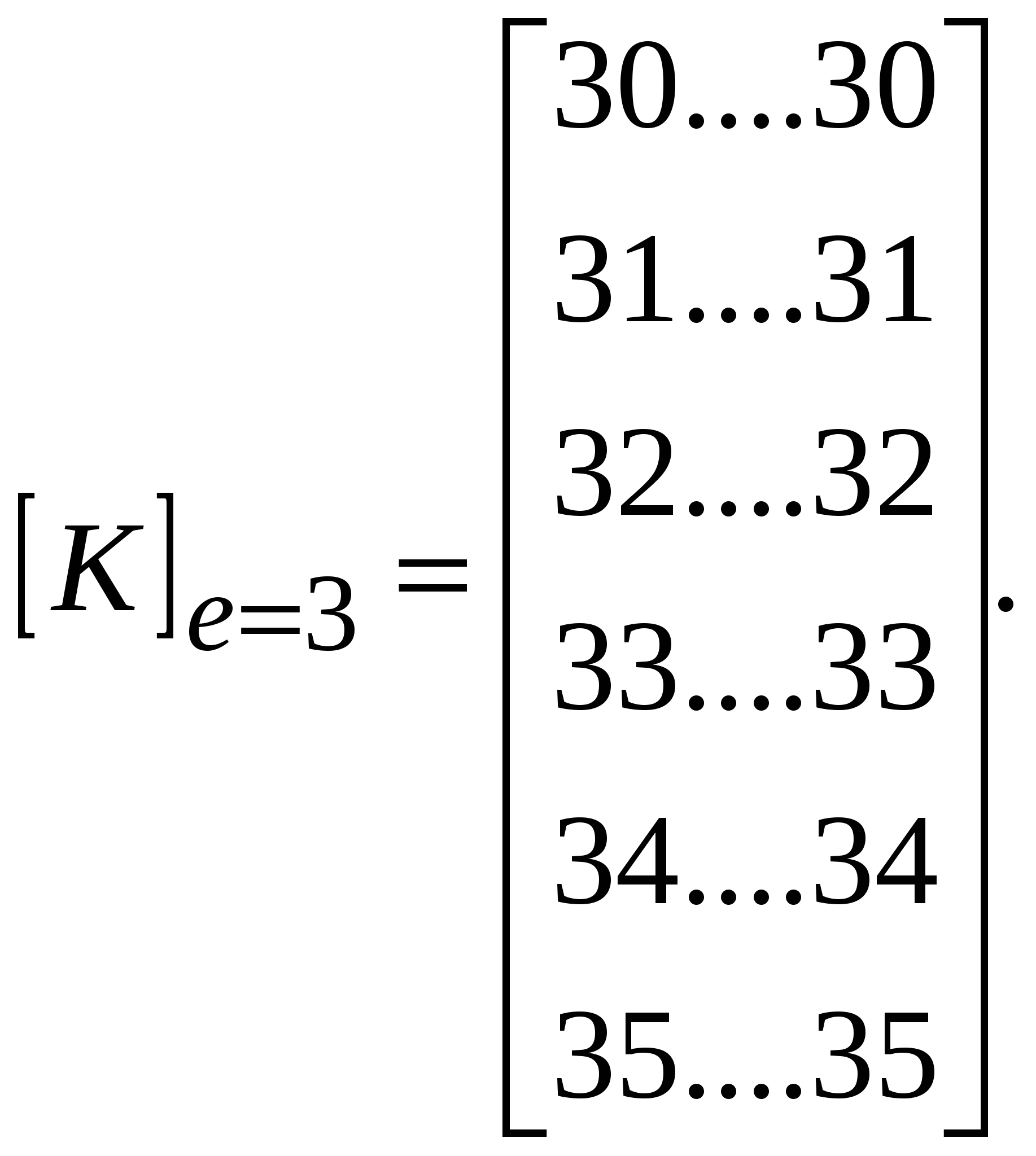 Составим сумму внутренних сил, действующих на третий узел в направлении оси ОХ: 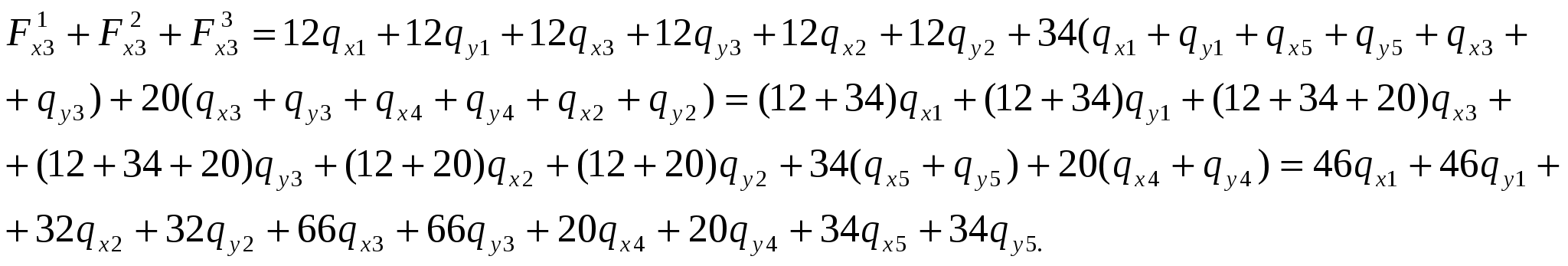 Вектор строка: Вектор строка:[46 46 32 32 66 66 20 20 34 34] (1) – представляет собой одну из строк матрицы жесткости [К], К5,j – значения компонент этой строки получены присвоением значениям соответствующих компонентов матриц жесткости окружающих элементов или их сложением (сложением коэффициентов при одинаковых q). Каждую компоненту матрицы жесткости [K] можно рассчитать по формуле: где l – число окружающих узел элементов; Процедура формирования матрицы [К] способом объединения по узлам: Procedure Rachet_matrSt; Var m1, m2, m3, m4, m5, m6: byte; Begin for i:=1 to 2*col_uzlov do for j:=1 to 2*col_uzlov do st[i]^[j]:=0; for n:=1 to kol_uzlov do begin for k:=1 to 9 do begin L:=uzel_elem[n,k]; if l>0 then begin m1:=nod[L,1]*2-1;m2:=nod[L,1]*2; m3:=nod[L,2]*2-1;m4:=nod[L,2]*2; m5:=nod[L,3]*2-1;m6:=nod[L,3]*2; if n=nod[L,1] then begin st[2*n-1, m1]:=st[2*n-1, m1]+ste[L, 1, 1]; st[2*n, m1]:=st[2*n, m1]+ste[L, 2, 1]; st[2*n-1, m2]:=st[2*n-1, m2]+ste[L, 1, 2]; ………………………………………………*8раз st[2*n, m6]:=st[2*n, m6]+ste[L, 2, 6]; end; if n=nod[L,2] then begin st[2*n-1, m1]:=st[2*n-1, m1]+ste[L, 3, 1]; st[2*n, m1]:=st[2*n, m1]+ste[L, 4, 1]; st[2*n-1, m2]:=st[2*n-1, m2]+ste[L, 3, 2]; ………………………………………………*8раз st[2*n, m6]:=st[2*n, m6]+ste[L, 4, 6]; end; if n=nod[L,3] then begin st[2*n-1, m1]:=st[2*n-1, m1]+ste[L, 5, 1]; st[2*n, m1]:=st[2*n, m1]+ste[L, 6, 1]; st[2*n-1, m2]:=st[2*n-1, m2]+ste[L, 5, 2]; ………………………………………………*8раз st[2*n, m6]:=st[2*n, m6]+ste[L, 6, 6]; end;end;end;end;end; Формирование матрицы жесткости способом объединения по элементам заключается в построении расширенных матриц жесткости с последующим их сложением. Расширенная матрица жесткости элемента [K]i,p строится из матрицы жесткости [K]i конечного элемента. Ненулевые компоненты матрицы [K]i,р равны компонентам [K]i, причем положение каждой компоненты матрицы [K]i в матрице [K]i,р определяется по номерам узлов составляющих i-й элемент (см. рис. 2). 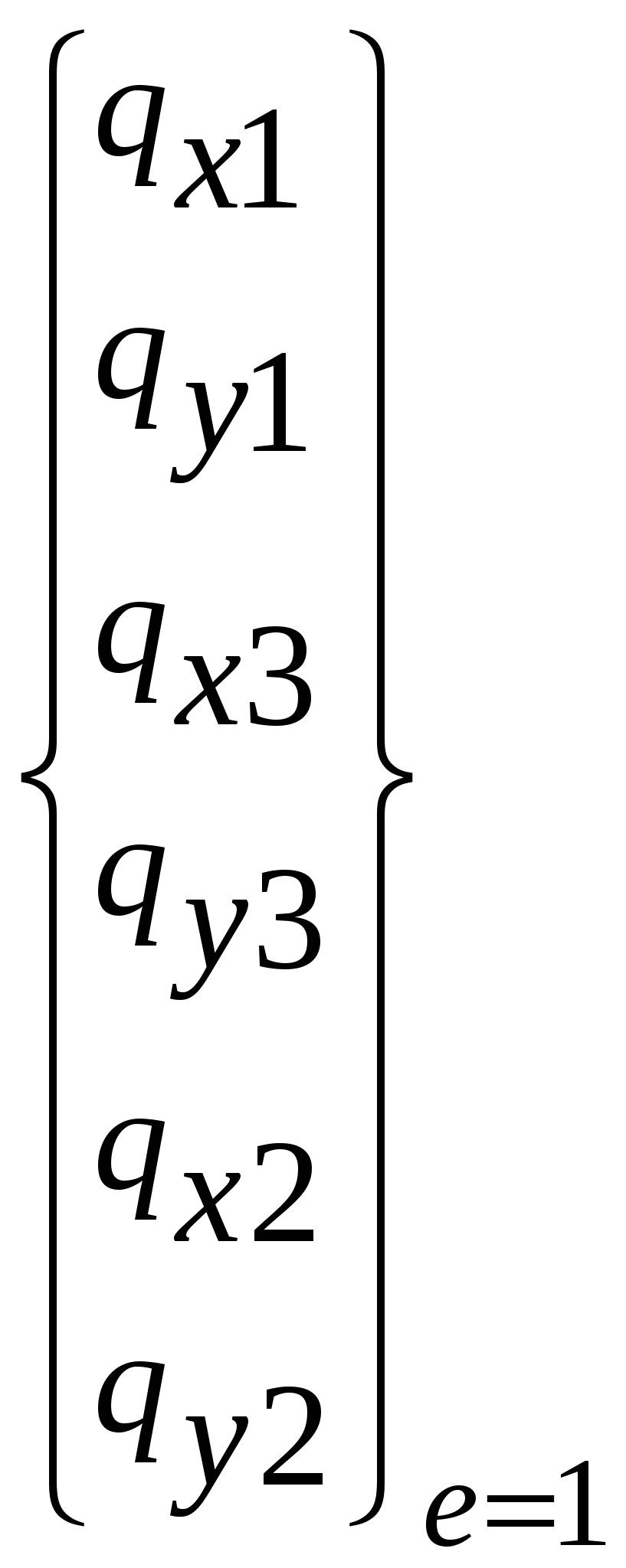 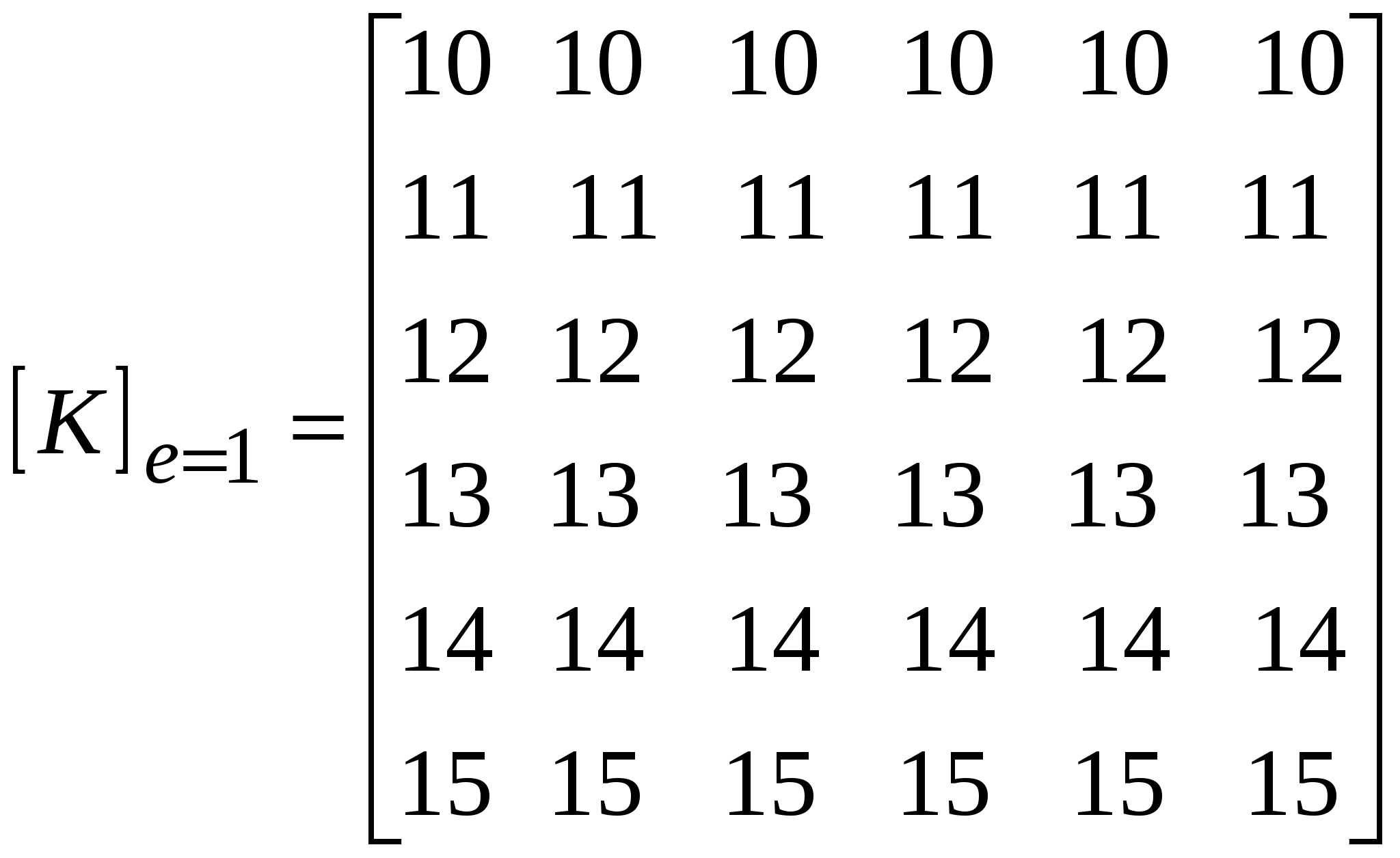 в 2*1-1 ую строку в 2*1 ую строку в 2*3-1 ую строку в 2*3 ую строку в 2*2-1 ую строку в 2*2 ую строку              Рис. 2. Схема к построению расширенной матрицы жесткости |
