|
Преподаватель - Боткин А.В. Преподаватель - Боткин А. Решение организационных вопросов, вопросов техники безопасности, расчет ожидаемого экономического эффекта
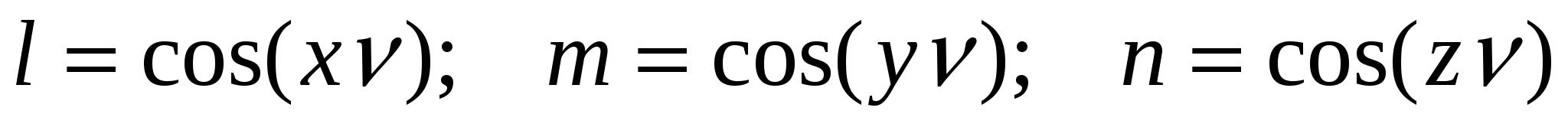
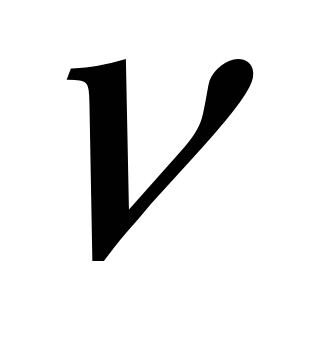 - нормаль к боковой поверхности элемента (поверхности контакта с подвижным инструментом). - нормаль к боковой поверхности элемента (поверхности контакта с подвижным инструментом).
Интеграл (1) при условии постоянства напряжений по элементу можно заменить суммой:
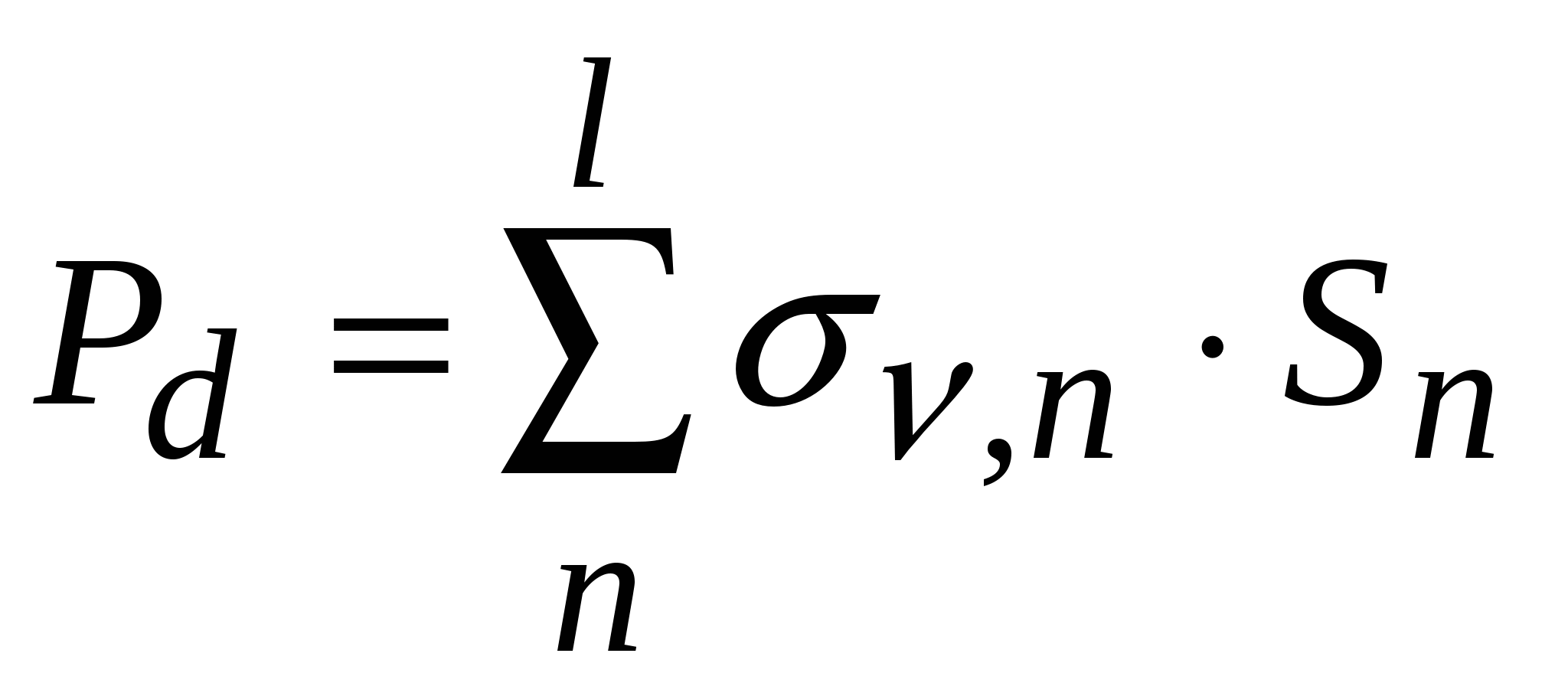 , ,
где нормальное контактное напряжение окрестности n-го конечного элемента;
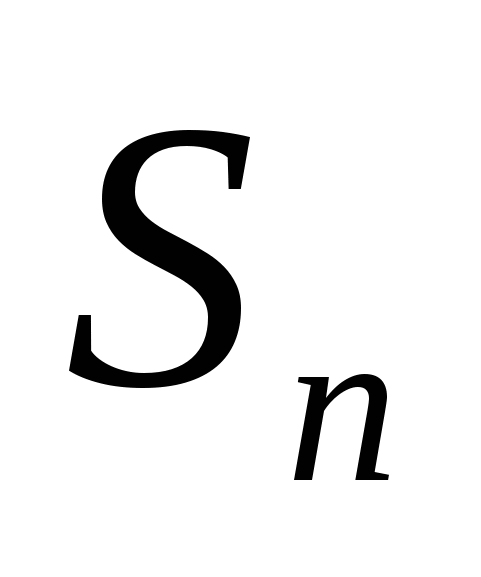 - проекция боковой поверхности элемента (поверхности контакта с подвижным инструментом) на плоскость, перпендикулярную вектору перемещения инструмента (см. рис. 5); - проекция боковой поверхности элемента (поверхности контакта с подвижным инструментом) на плоскость, перпендикулярную вектору перемещения инструмента (см. рис. 5);
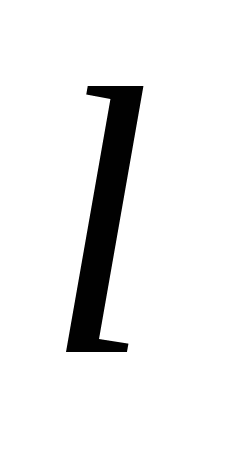 - количество граничных конечных элементов. - количество граничных конечных элементов.
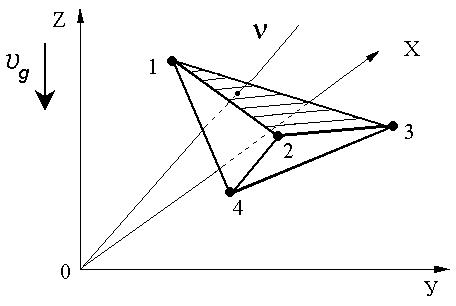
Рис.5
Площади S проекций поверхностей элементов, направляющие косинусы 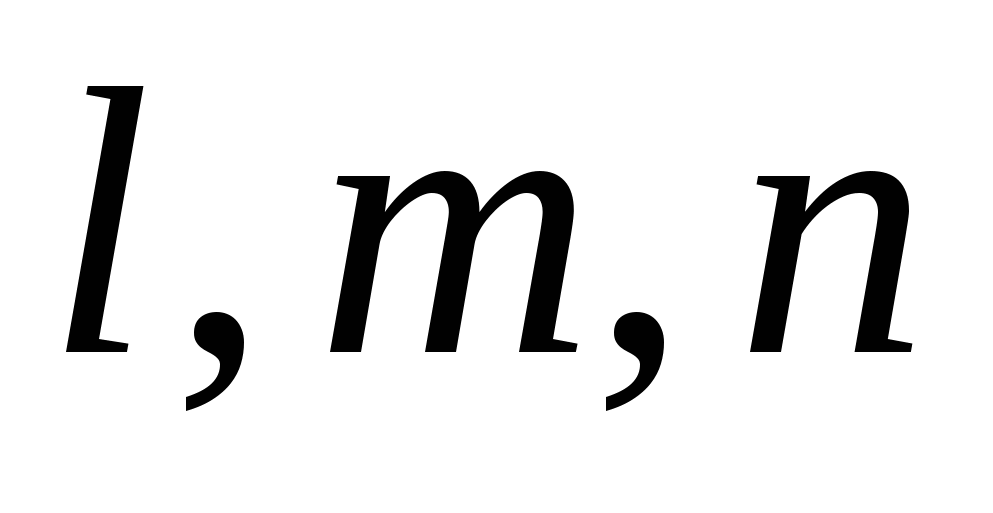 по координатам узлов. по координатам узлов.
При решении осесимметричной задачи и применении кольцевых контактных элементов площади проекций S представляют собой площади колец (рис. 6), а 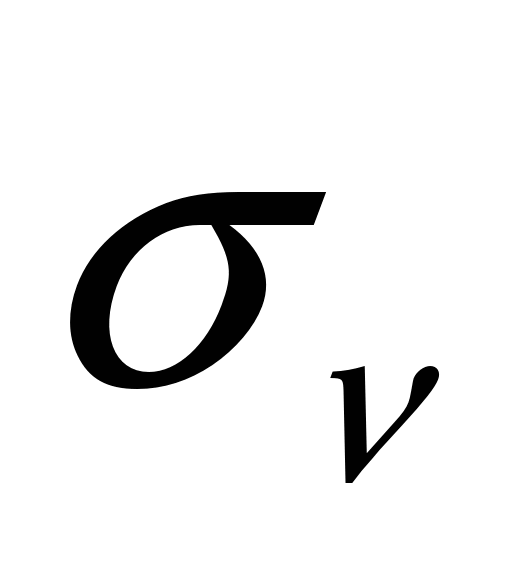 рассчитывают по формуле: рассчитывают по формуле:
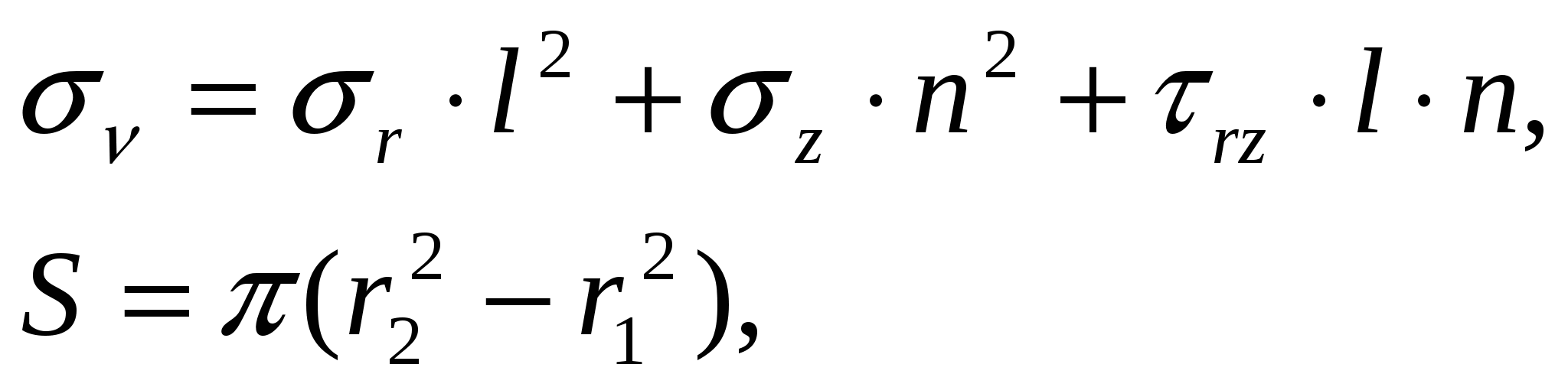
где 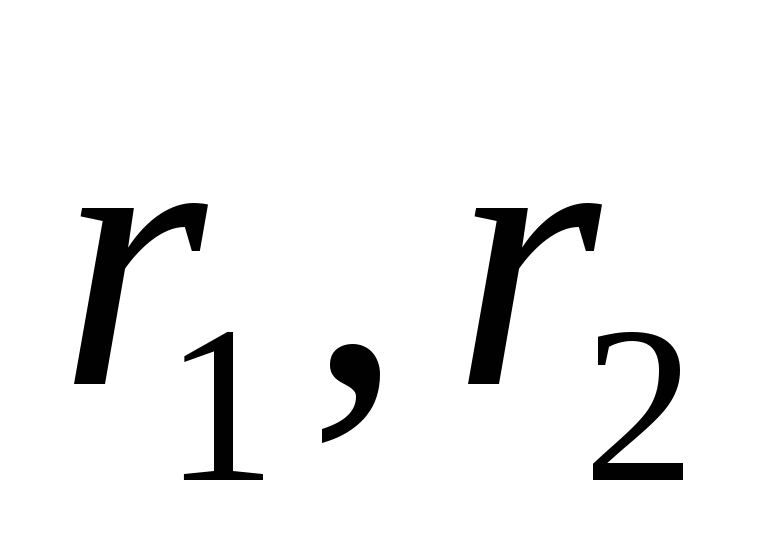 - радиусы узлов 1 и 2 (узлы 1,2,3 – определяют кольцевой контактный элемент). - радиусы узлов 1 и 2 (узлы 1,2,3 – определяют кольцевой контактный элемент).
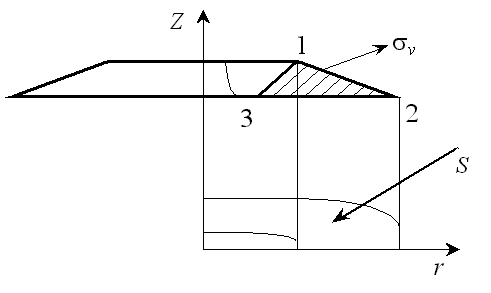
Рис.6
В случае упругопластического метода конечных элементов значения перемещения подвижного штампа, соответствующее к-му этапу нагружения конечно элементной модели, рассчитывают по формуле:
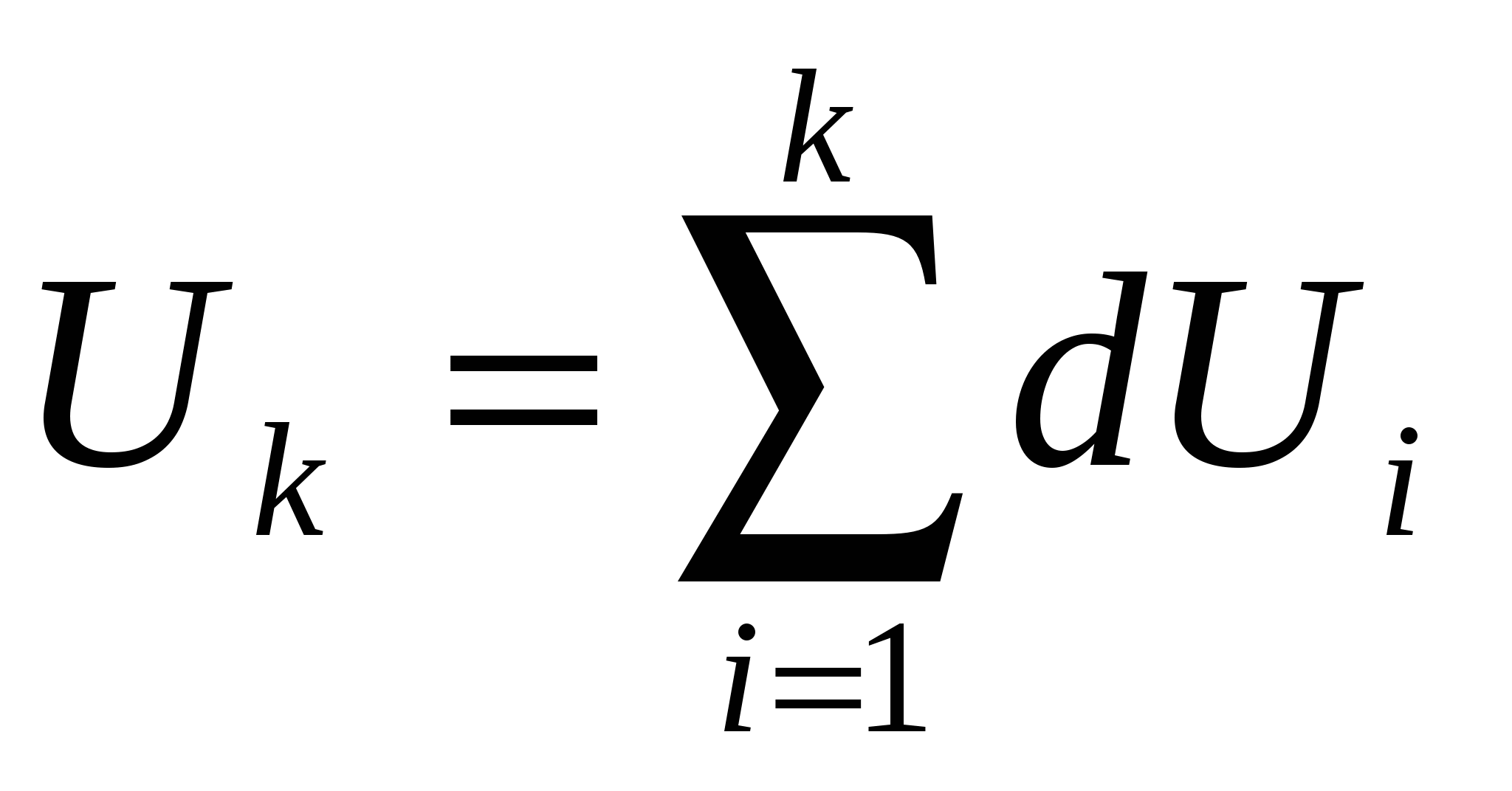 , ,
где 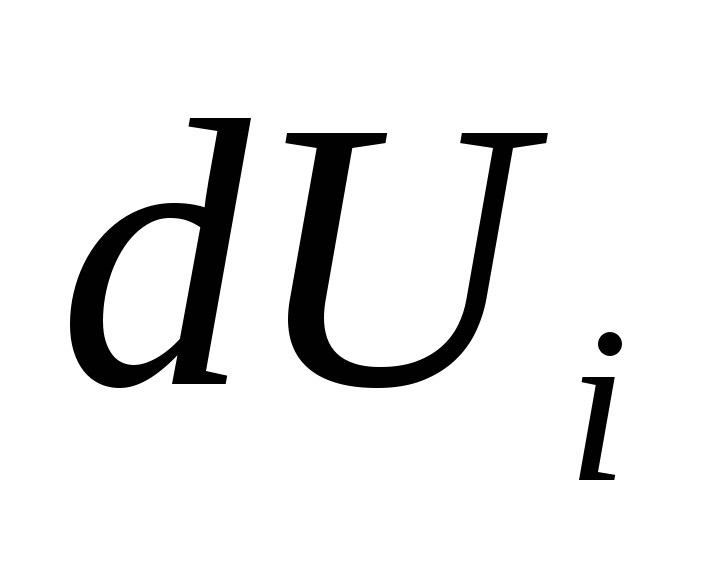 - значения приращения перемещения подвижного штампа на i-ом этапе нагружения (обычно эту величину - часть от полного перемещения, принимают в расчете постоянной для всех этапов нагружения из интервала: 0.001÷0.1 мм). - значения приращения перемещения подвижного штампа на i-ом этапе нагружения (обычно эту величину - часть от полного перемещения, принимают в расчете постоянной для всех этапов нагружения из интервала: 0.001÷0.1 мм).
Точку с координатами (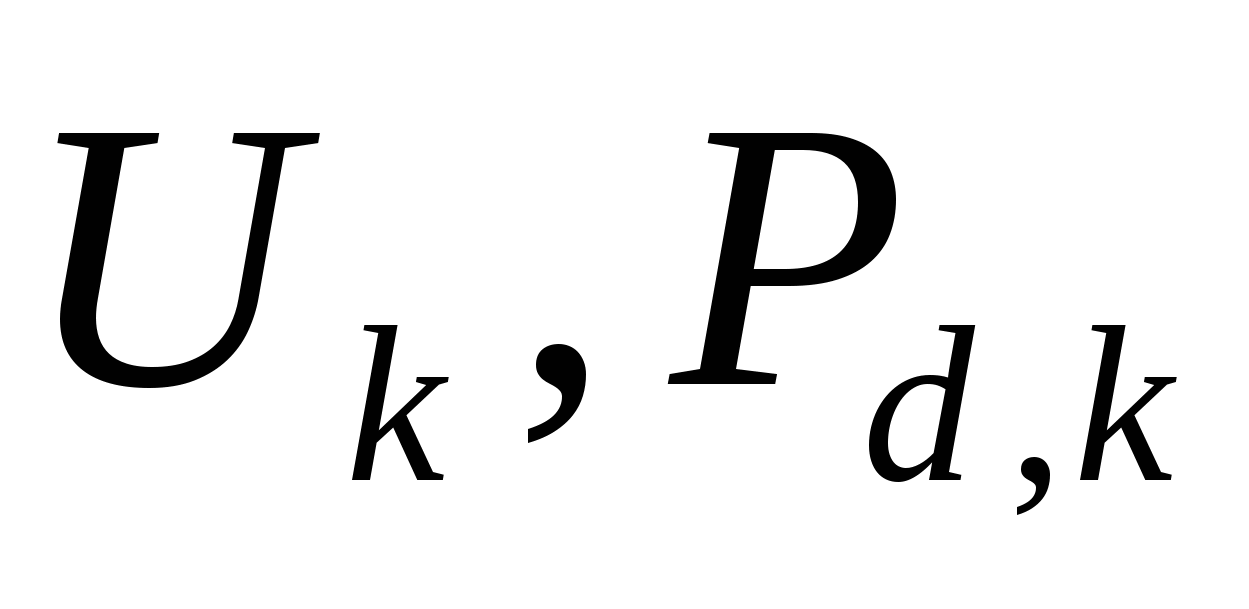 ) отмечают на координатной плоскости. ) отмечают на координатной плоскости.
Указанным образом рассчитывают 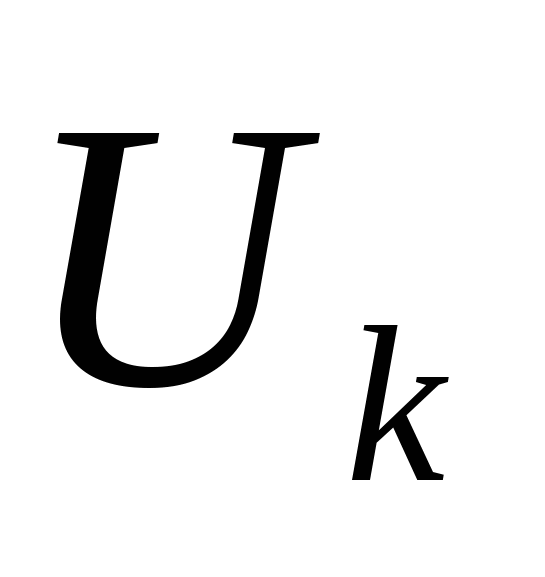 и и 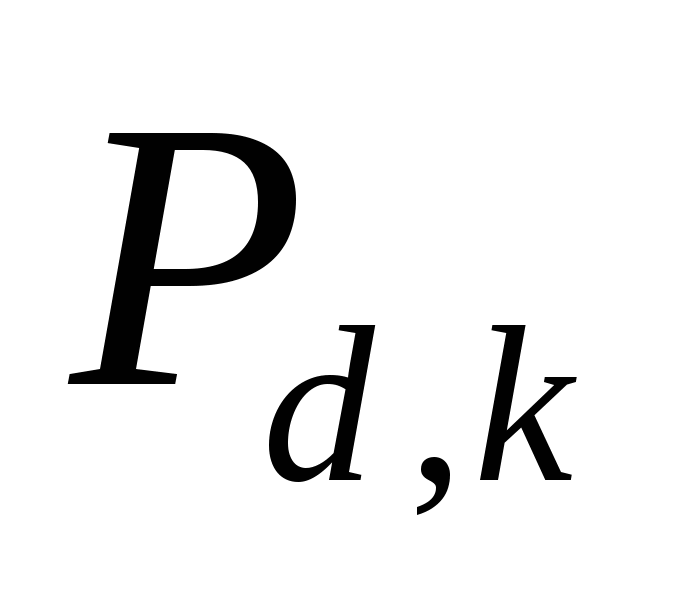 после намеченного этапа нагружения в соответствии с принятым шагом разрешения по времени полного формоизменения заготовки (100 точек на графике, 10 точек или иначе). после намеченного этапа нагружения в соответствии с принятым шагом разрешения по времени полного формоизменения заготовки (100 точек на графике, 10 точек или иначе).
График технологических нагрузок 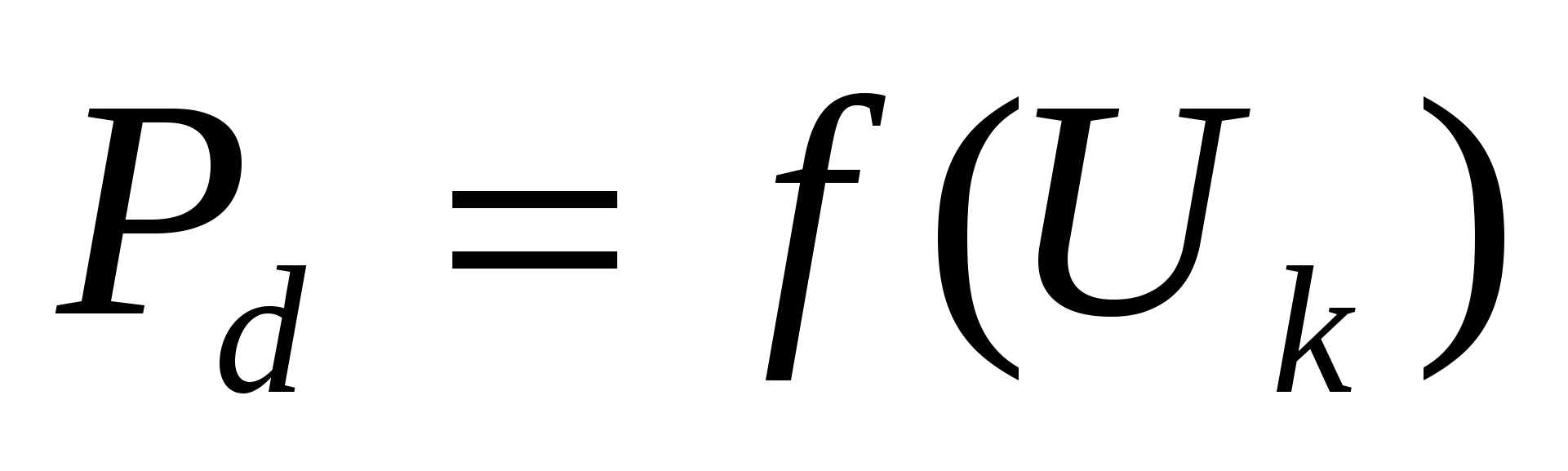 имеет большое значение при проектировании и выборе оборудования и инструмента формоизменения заготовки. имеет большое значение при проектировании и выборе оборудования и инструмента формоизменения заготовки.
Обычно при разработке технологических процессов ОМД график 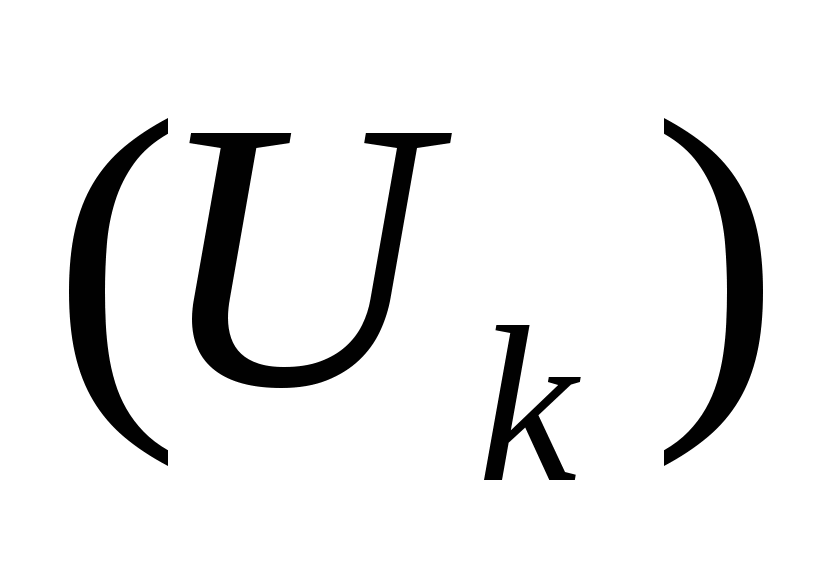 сравнивают с графиком допустимых нагрузок и принимают решение о целесообразности использования данного оборудования. сравнивают с графиком допустимых нагрузок и принимают решение о целесообразности использования данного оборудования.
Расчет поврежденности металла в различных местах конечно-элементной модели заготовки с применением феноменологической модели разрушения.
Напомним, что при использовании теории течения в приращениях перемещений результатом расчета после каждого этапа нагружения конечно элементной модели являются: приращения деформаций, приращения напряжений, полные напряжения. При этом если используются конечные элементы в форме треугольника (кольца с треугольным поперечным сечением), тетраэдра то эти характеристика одинаковы для всех точек составляющих конечный элемент, т.е. для таких конечных элементов Н.Д.С. которых однородно по элементу.
Напомним что при использовании феноменологической теории разрушения для расчета накапливаемой поврежденности необходимо кроме НДС и еще так называемые базовые уравнения [1].
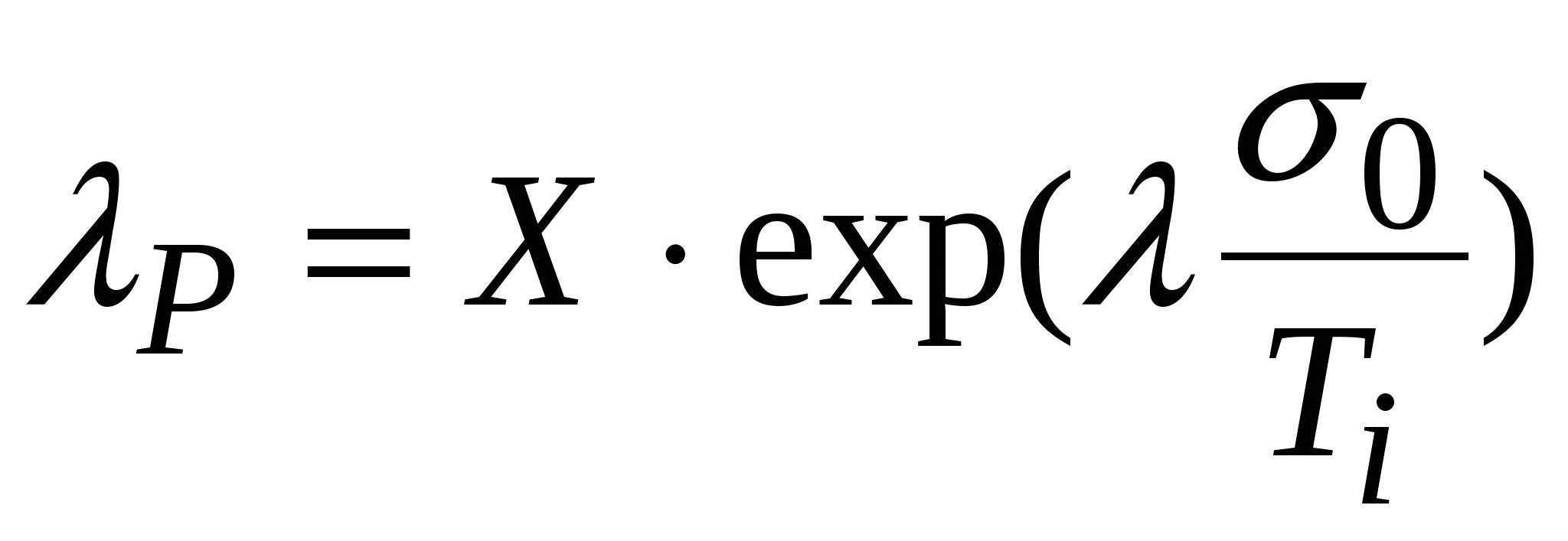 , (1) , (1)
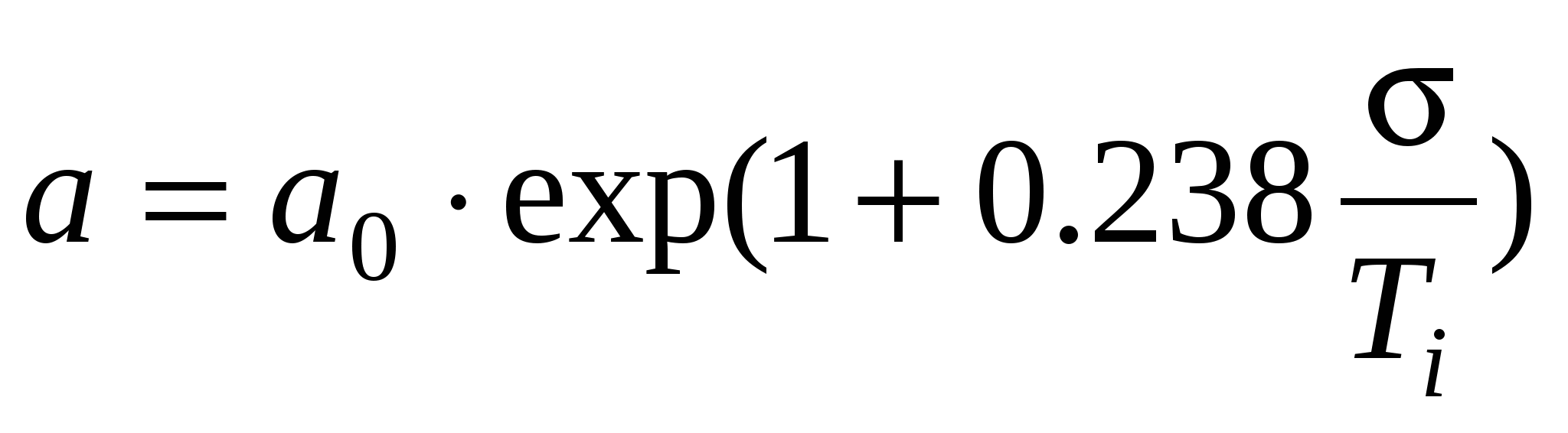 , (2) , (2)
где 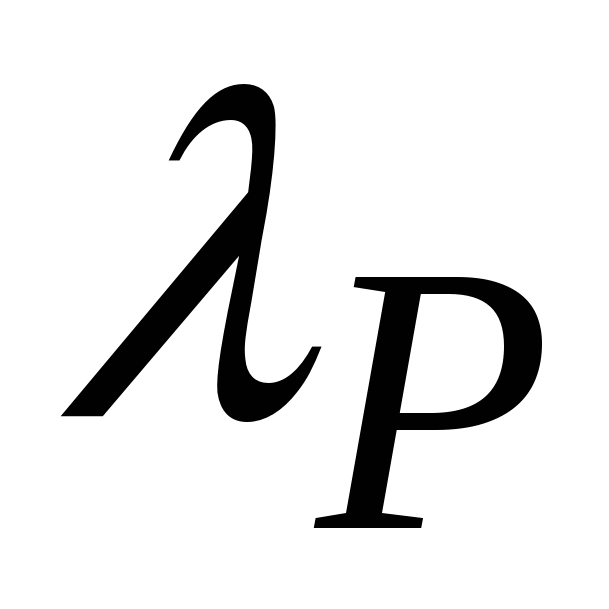 - функция, описывающая пластичность металла (см. рис.7), - функция, описывающая пластичность металла (см. рис.7), 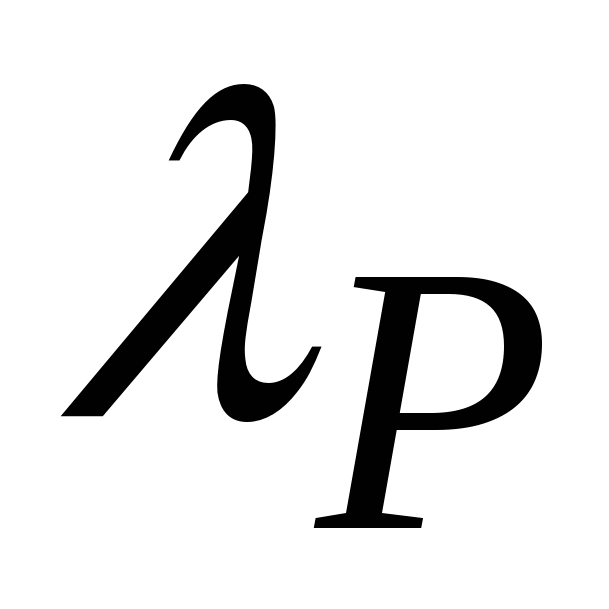 – предельно возможная холодная деформация металла без разрушения при отношении- σ0/Ti, σ0 - среднее напряжение, Ti – интенсивности касательных напряжений. – предельно возможная холодная деформация металла без разрушения при отношении- σ0/Ti, σ0 - среднее напряжение, Ti – интенсивности касательных напряжений.
Ti=Ts=σs/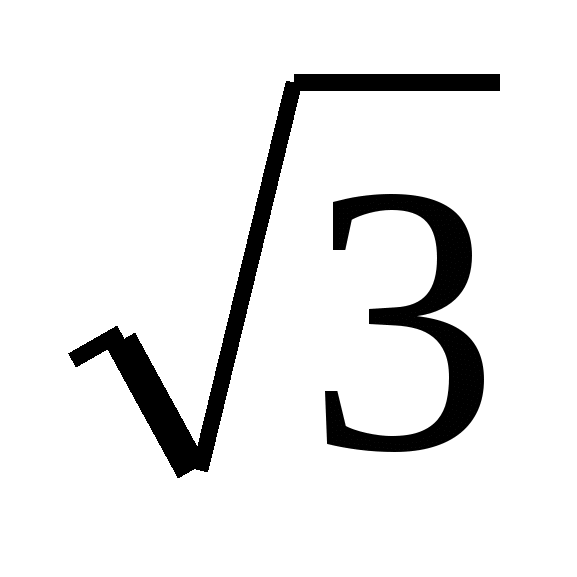 , Ts – напряжение течения металла при сдвиге, σs- напряжение течения металла при сжатии или растяжении, определяется по диаграмме деформирования σs (εi) в соответствии с накопленной мат. частицей деформацией εi, , Ts – напряжение течения металла при сдвиге, σs- напряжение течения металла при сжатии или растяжении, определяется по диаграмме деформирования σs (εi) в соответствии с накопленной мат. частицей деформацией εi,
λ – коэффициент зависит от материала,
x – также коэффициент зависит от рода материала,
a0 - зависит от рода материала.
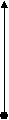 σ/Ti σ/Ti

 Λp Λp
Рис.7.
Выражения для расчета поврежденности частицы, рассчитывают по формуле:
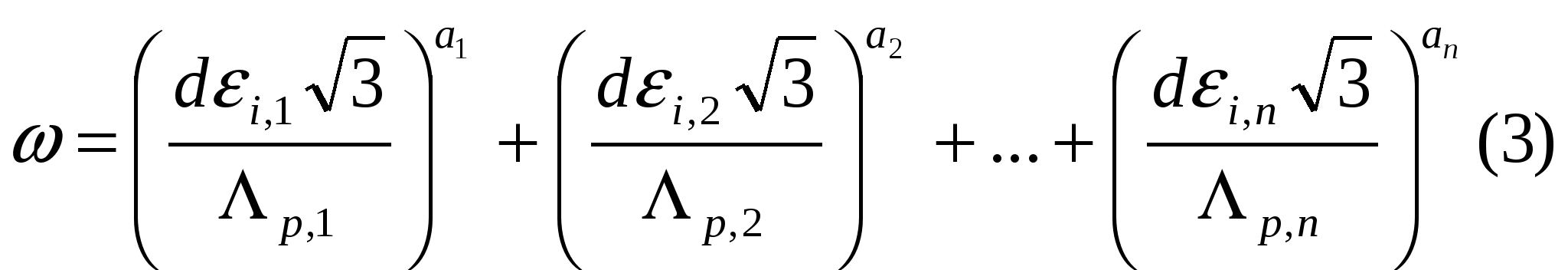
где dεi,n – интенсивность приращений деформаций мат. частицы (интенсивность, полученная на n – ом этапе нагружения)
an – коэффициент рассчитывается по зависимости (2) с учетом отношения σ0/Ti для n-го этапа нагружения частицы
Λp,1 Λp,2 ... и т. д. рассчитывается по зависимости (1) для 1, 2 и т. д. этапов нагружения.
Интенсивности приращений деформаций рассчитывается как:
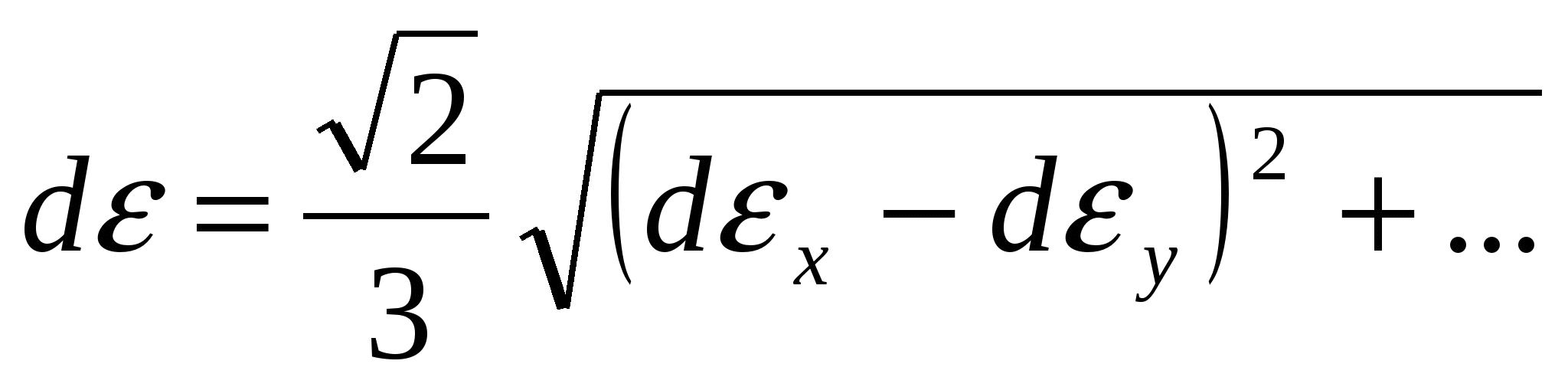 (4) (4)
по компонентам приращений деформаций.
Легко представить алгоритм использования зависимостей (1...4) при моделировании пластического формоизменения заготовки методом конечных элементов.
При использовании треуг. элементов или элементов в форме тетраэдра (Н.Д.С.- однородно) расчет поврежденности возможен для каждого конечного элемента.
При этом расчет возможен после каждого этапа нагружения или после группы этапов.
dεi,m=Σdεi,n, где k – количество этапов нагружения, после которых рассчитывается поврежденность в m-ом элементе.
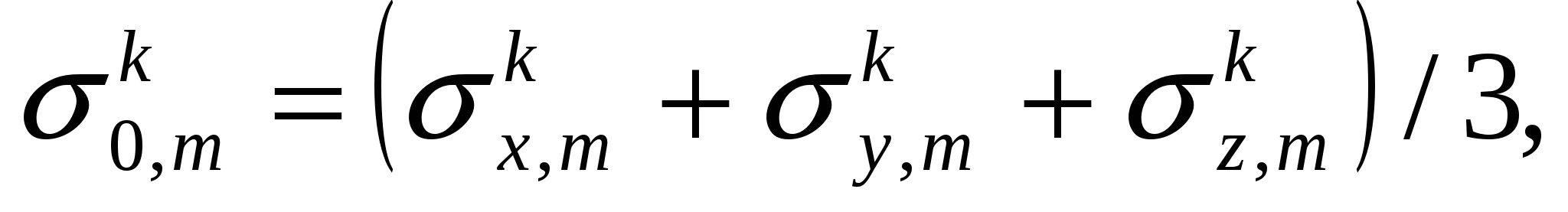
σk0,m – среднее напряжение в m-ом элементе после k-го шага нагружения.
Ti,mk – оценивает по диаграмме деформирования с учетом εi,mk, то есть по зависимости σs(εi) 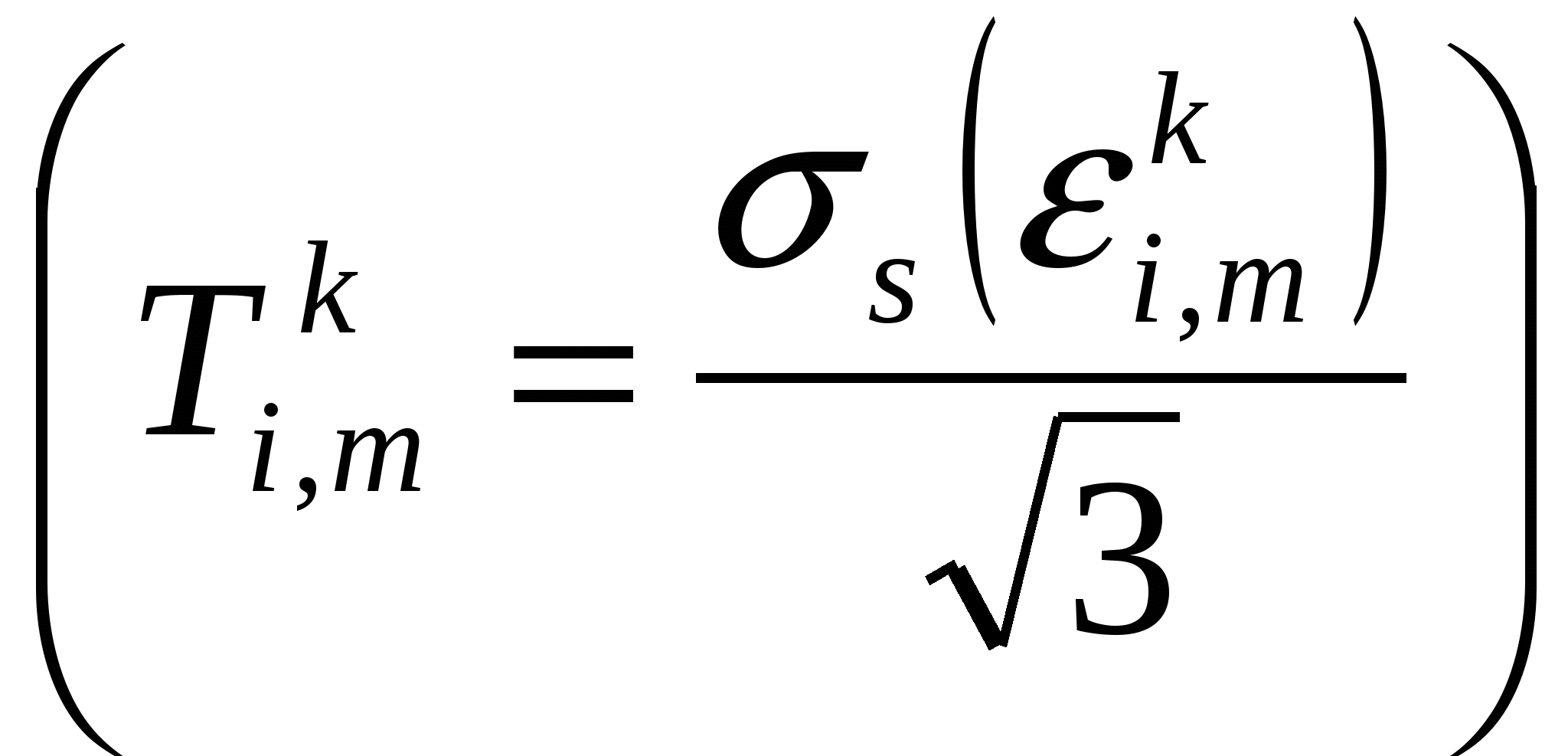
Расчет Λp,mk и amk по зависимости (1), (2).
Расчет ωmk поврежденности после k-го нагружения в m-ом элементе по зависимости (3).
Коэффициенты a0, x, λ базовых уравнений для некоторых марок сталей и сплавов приведены в [1].
Ресурс пластичности металлов при обработке давлением. Богостов А.А., Мигушрицкий О.И., Смирнов С.В. - М., Металлургия, 1984, 144с.
На кафедре ОМД разработана приближенная физическая модель разрушения металла в процессе холодной пластической деформации [2]
Грешнов В.М. , Боткин А.В. Применение физических моделей скалярных свойств в металле при постановке и решении краевых задач теории пластичности // Проблемы машиностроения и надежности машин. – 1999 - №5 – с. 31-37.
В соответствии с этой моделью приращение поврежденности металла (приращение плотности микротрещин) на этапе нагружения материальной частицы оценивается по формуле:
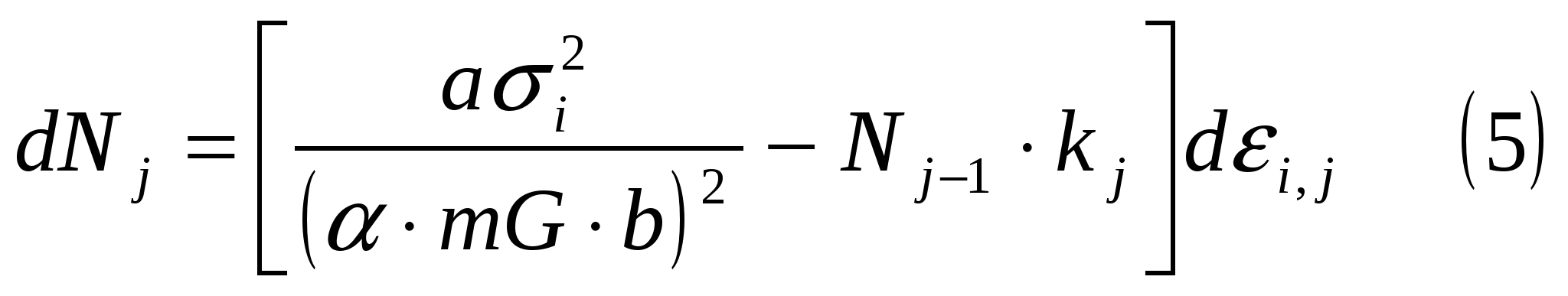 , ,
где σi=σs, интенсивность напряжений, равна мгновенному пределу текучести, рассчитывается по диаграмме деформирования с учетом накопленной деформации εi (если диаграмма описана зависимостью вида σs(εi), то по этой зависимости, а – коэфф-т, α, m, G, b – физические параметры, значения которых обусловлено металлом).
Для стали 20: α=0,22; m=3,1; G=8500кгс/мм2 ; b=3·10-7мм; Nj-1 – плотность микротрещин, накопленная частицей за предыдущие (j-1) этапов нагружения
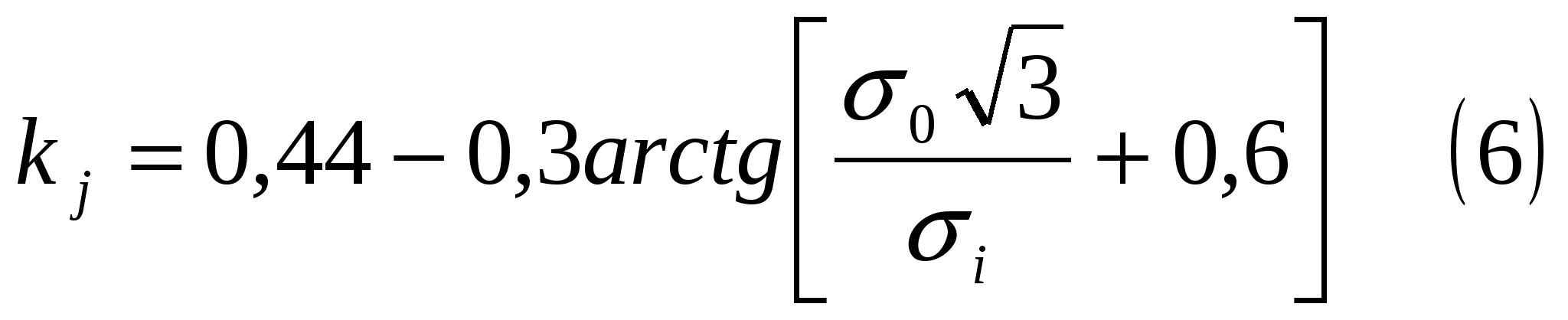
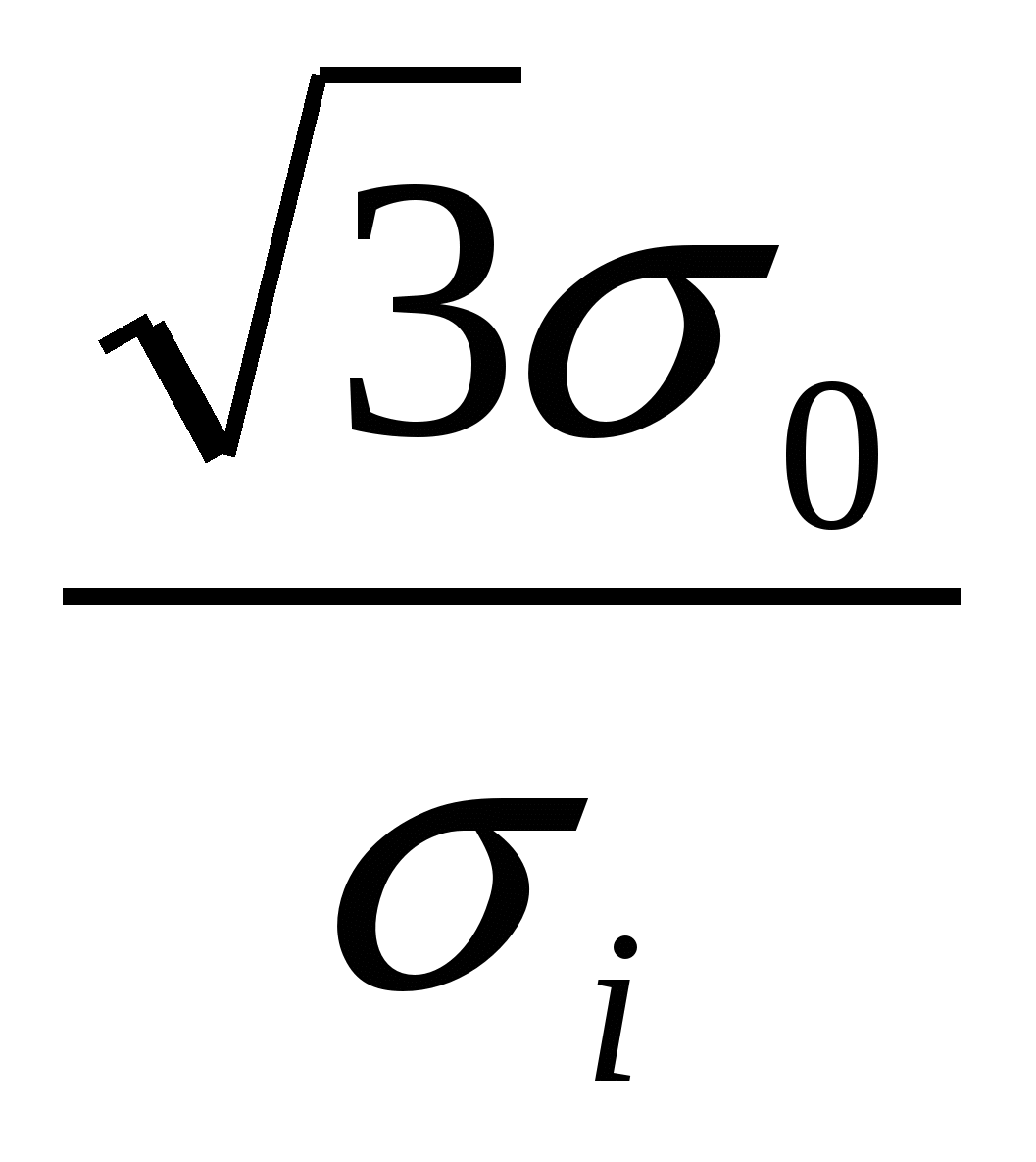 - показатель жесткости схемы напряженного состояния, σ0 – среднее напряжение на j-ом этапе нагружения матер. частицы. - показатель жесткости схемы напряженного состояния, σ0 – среднее напряжение на j-ом этапе нагружения матер. частицы.
Поврежденность после j-го этапа нагружения рассчитывают по формуле:
Nj=Nj-1+dNj (7)
По поврежденности оценивают степень использования ресурса пластичности:
Ψ=Nj/Nкр (8),
где Nкр – критическая плотность микротрещин для данного коэффициента жесткости, схемы напряжений и металла,
при 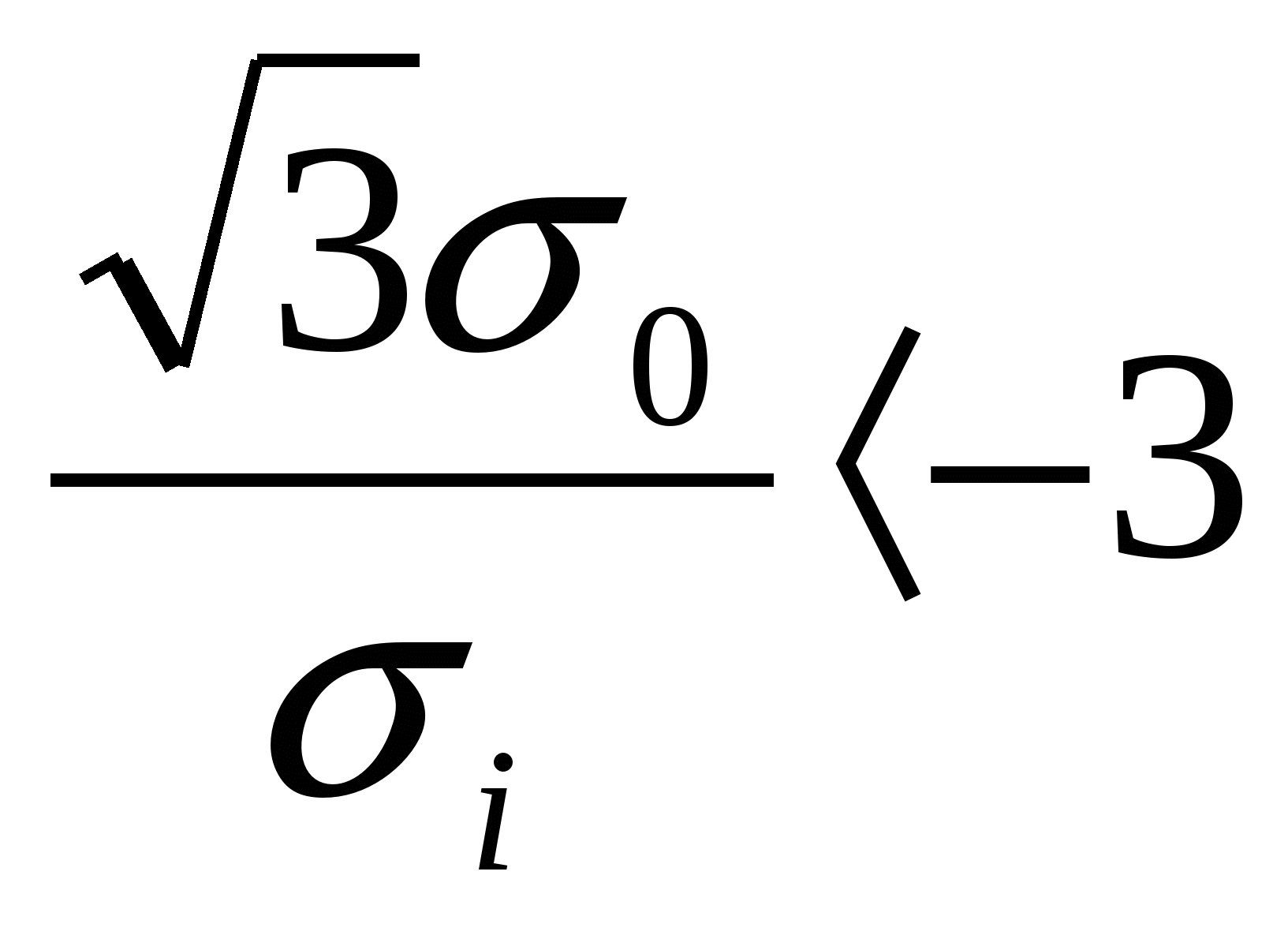 Nкр=105 мм-2 Nкр=105 мм-2
при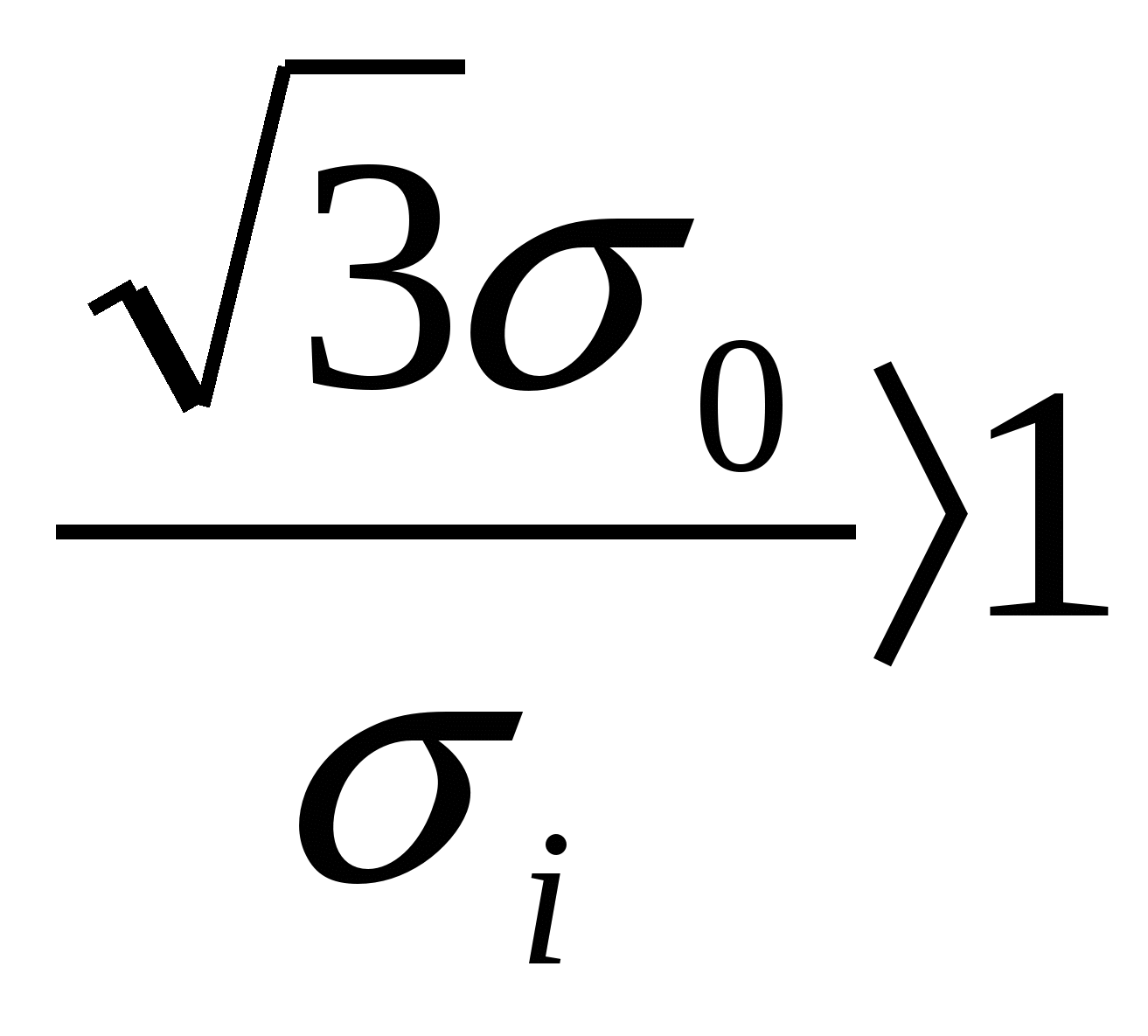 Nкр=104 мм-2 Nкр=104 мм-2
при 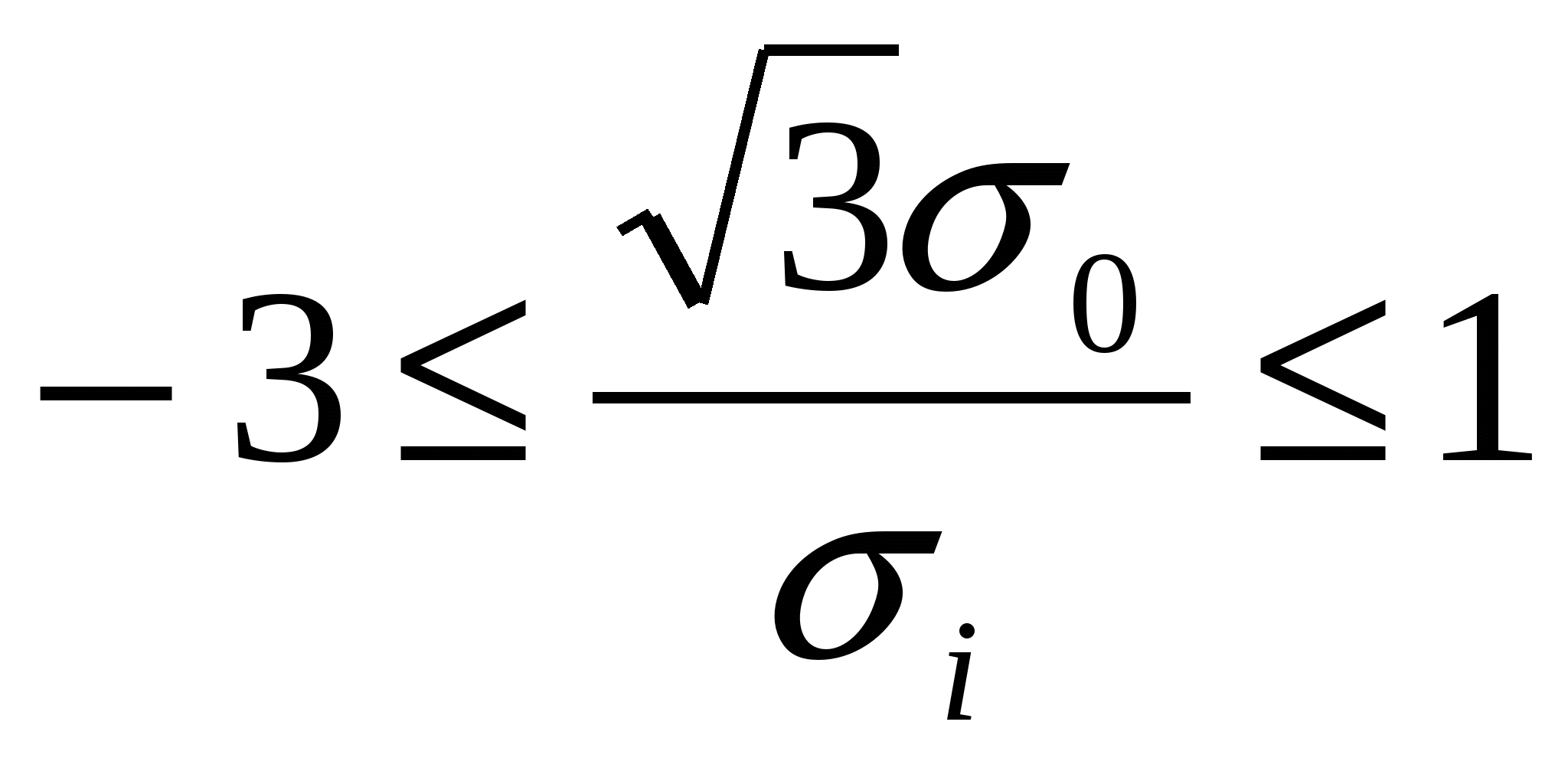 Nкр=-6·103[ Nкр=-6·103[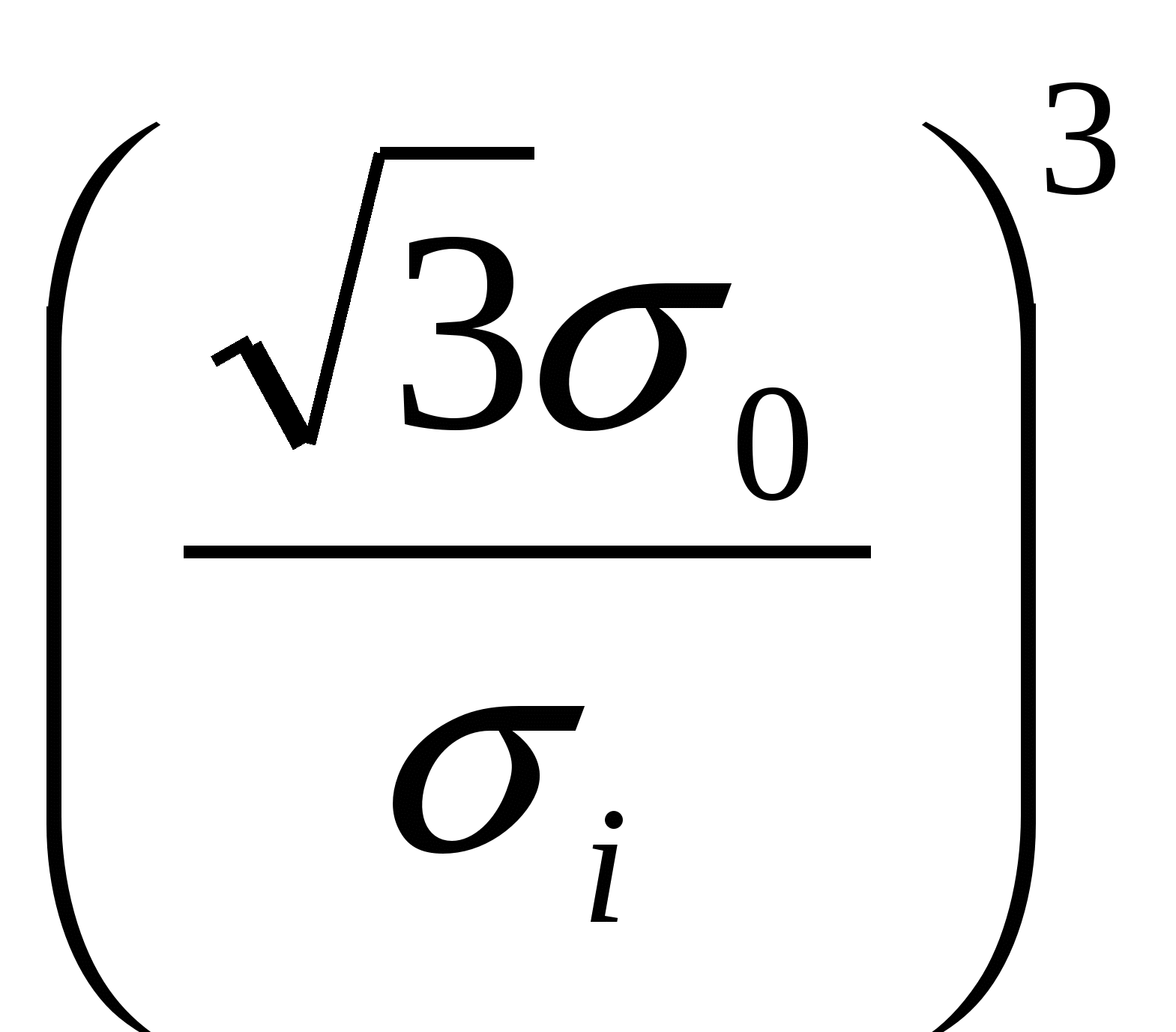 -3·104 -3·104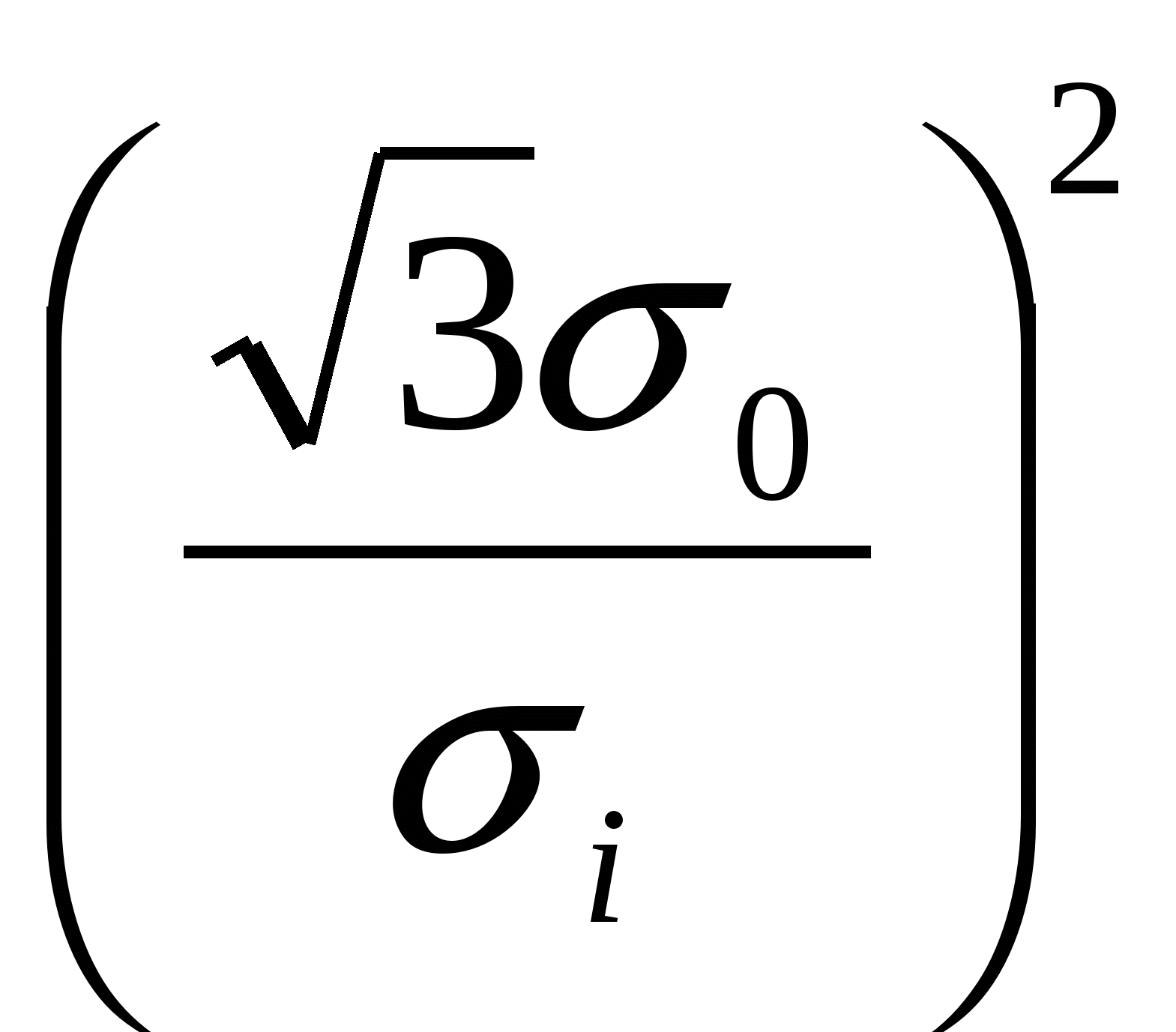 -3·104 -3·104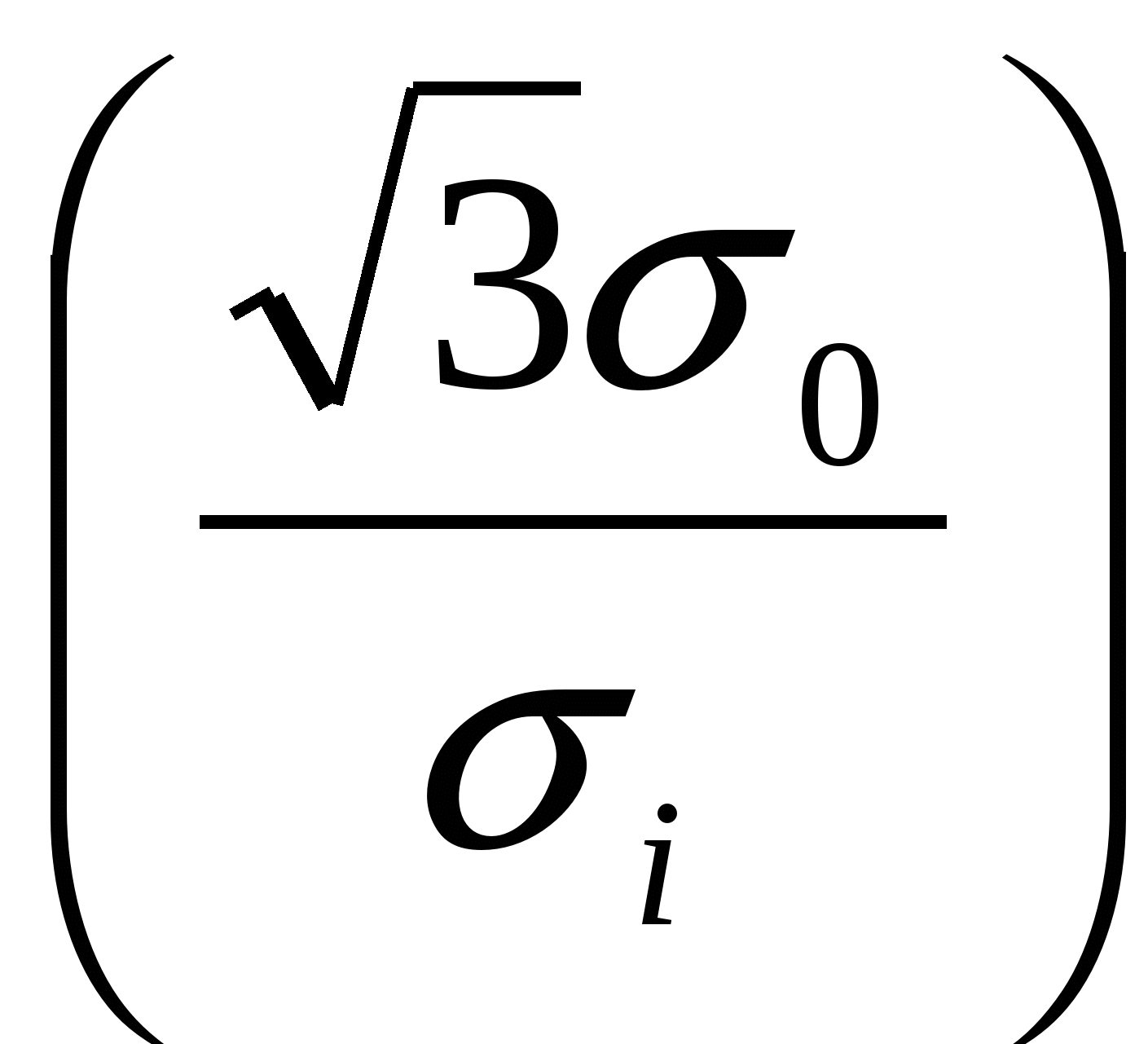 ]+f·104 [мм-2] ]+f·104 [мм-2]
В случае однородности НДС конечного элемента, расчет степени использования ресурса пластичности возможен также для каждого конечного элемента:
До первого этапа нагружения конечно-элементной модели поврежденности всех конечных элементов равны 0.
По окончанию очередного этапа нагружения для каждого конечного элемента расчет поврежденности проводится по следующему алгоритму:
Рассчитывается интенсивность приращений деформаций для элемента dεi на j этапе нагружения, накопленная деформация εi,m= Σdεi,m.
Рассчитывается среднее напряжение σ0=(σx+σy+σz)/3 и интенсивность напряжений σi по диаграмме деформирования σi(εi) для элемента.
По формуле (6) рассчитывается коэффициент ki.
По формуле (5) рассчитывается приращение плотности микротрещин dNi для элемента на j-ом этапе нагружения.
Рассчитывается плотность по формуле (7) и степень использования ресурса пластичности ψ по выражению (8).
Рассчитывается значение ψ после j-го этапа нагружения конечного элемента. Сравнивается с единицей для оценки возможности разрушения металла в окрестности конечного элемента.
Тема 9. Особенности применения метода конечных элементов для моделирования горя чего формоизменения металлических заготовок.
1. Вывод основной системы МКЭ для решения задачи в скоростях.
2. Линеаризация задачи пластичности решаемой методом МКЭ в скоростях.
3. Формирование исходных данных в части свойств.
а) для решения задачи в скоростях (диаграмма течения).
б) для решения задачи в приращениях перемещений
(диаграмма деформирования).
1. Основная система МКЭ при решении задачи в скоростях:
[К]*{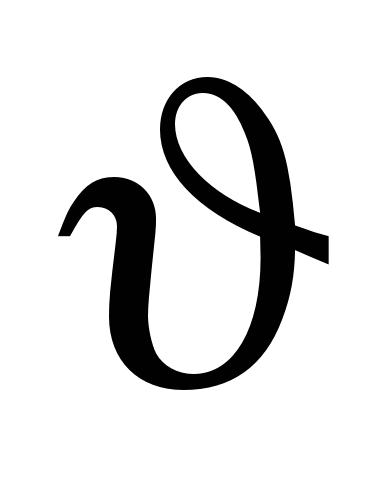 }={F}, }={F},
где [К]- матрица жесткости (матрица коэффициентов системы уравнений),
{V}- матрица столбец корней системы (корнями являются проекции узловых скоростей на оси координат).
Согласно методу баланса работ:
WПЛ.Д=WВ, (1)
где, WПЛ.Д – мощность пластической деформации,
WВ- мощность внешних сил приложенных к заготовке (включая силы трения).
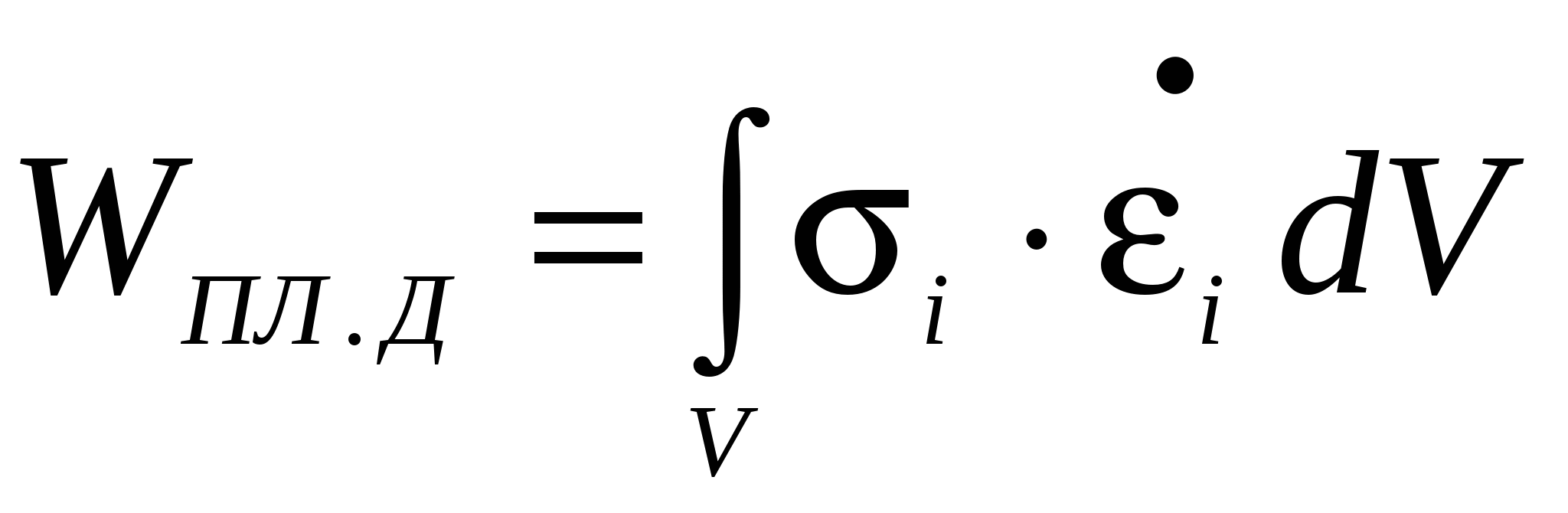 , или приближенно , или приближенно
где, I – интенсивность скоростей деформации,
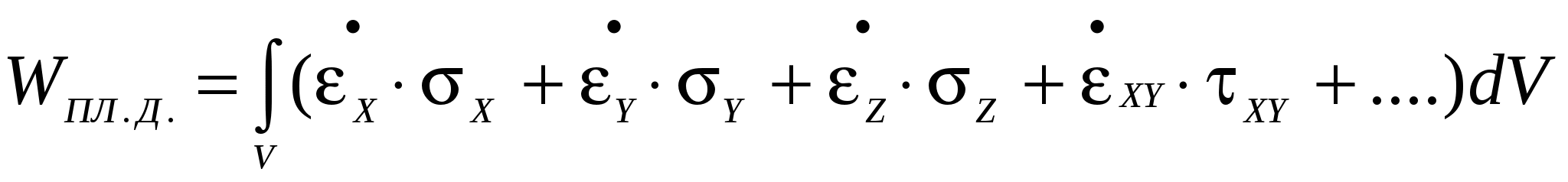
При конечно-элементном представлении тела выражение WПЛ.Д. можно записать иначе:
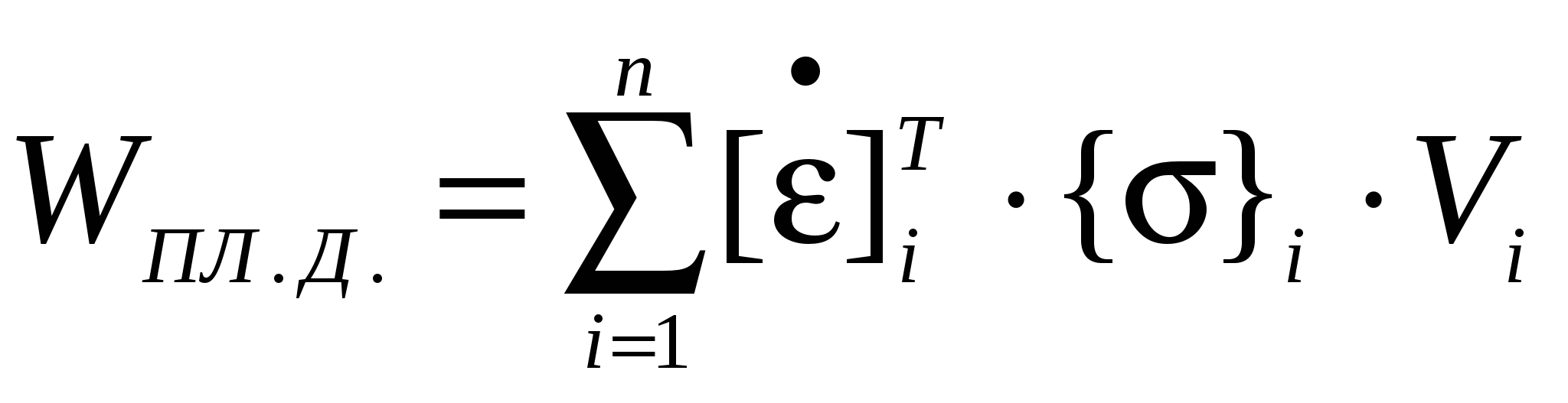 , (2) , (2)
где 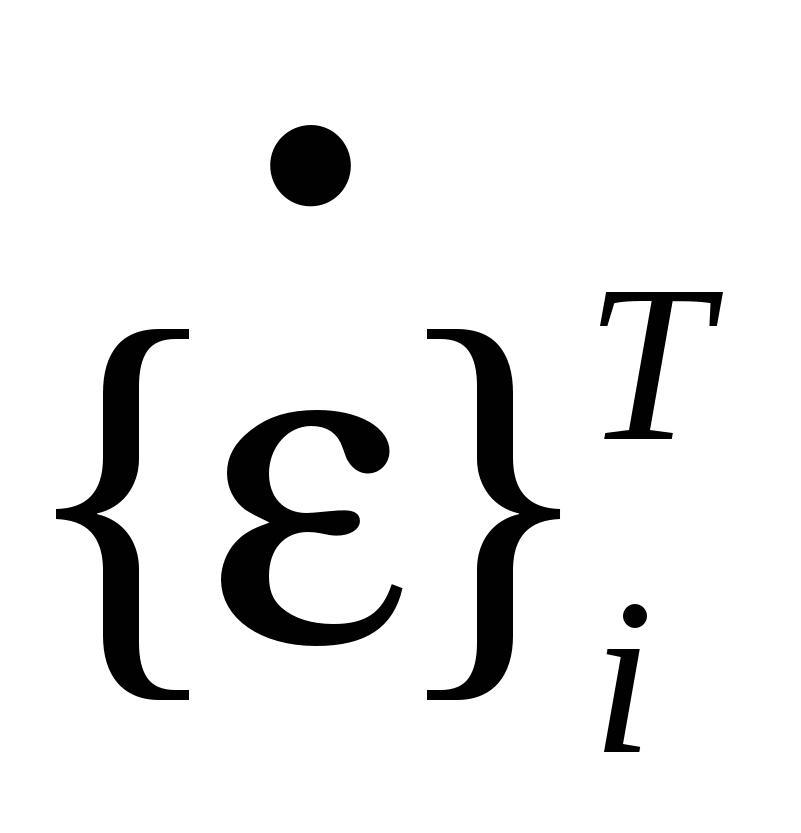 - матрица строка скоростей деформации i-го элемента полученная транспортированием матрицы столбца. - матрица строка скоростей деформации i-го элемента полученная транспортированием матрицы столбца.
{σ}- матрица столбец напряжений i-го элемента,
{Vi}- объем i-го элемента,
n- количество конечных элементов.
Отметим, что (2) правомерно при использовании конечных элементов
для которых {σ}i и {έ}i постоянных для всех точек составляющих конечный
элемент.
Напомним, что согласно методу МКЭ:
{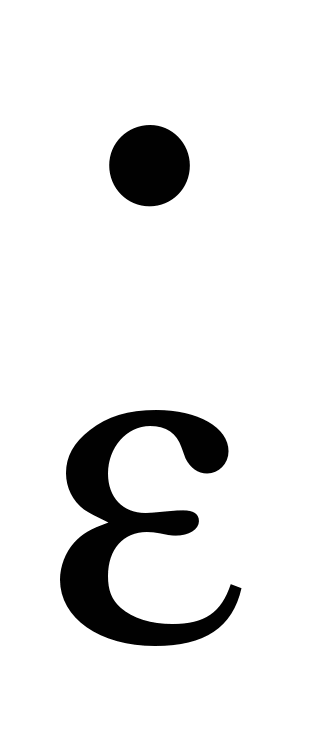 }Ti={ }Ti={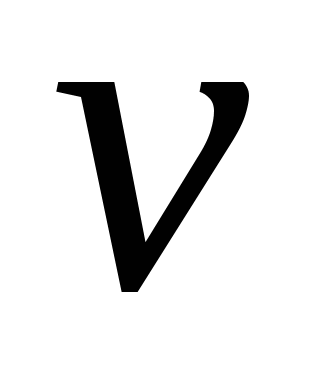 }Ti*[B]Ti , }Ti*[B]Ti ,
{σ}i=[D]i*[B]i*{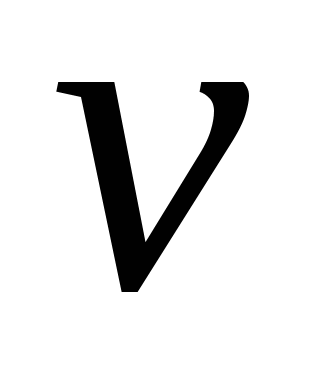 }i, }i,
Поэтому выражение (2) окончательно принимает вид:
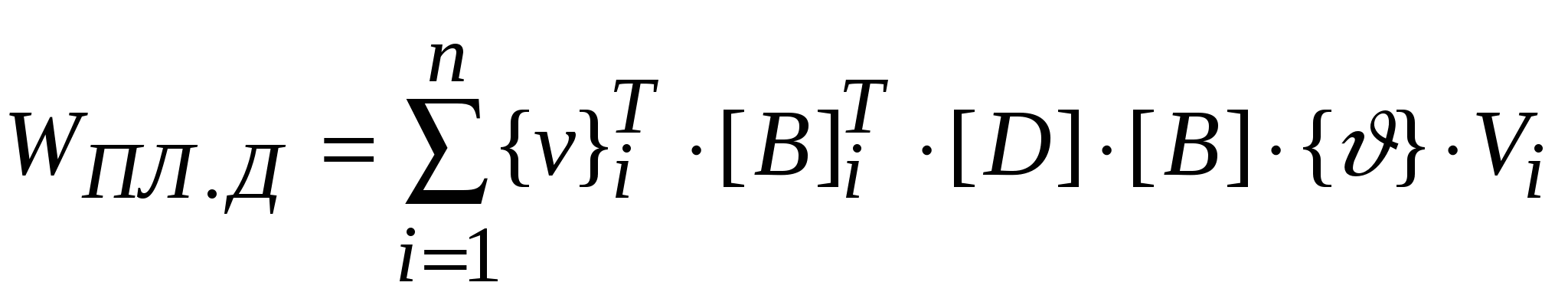 , (3) , (3)
Мощность внешних сил:
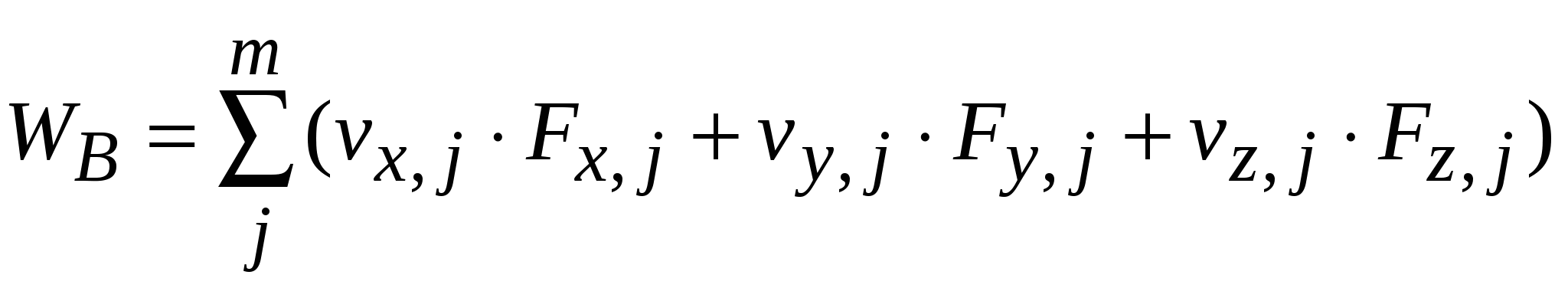 , (4) , (4)
где m- количество узлов нагруженных внешними силами.
С учетом (3) и (4) составим из (1) энергетический функционал:
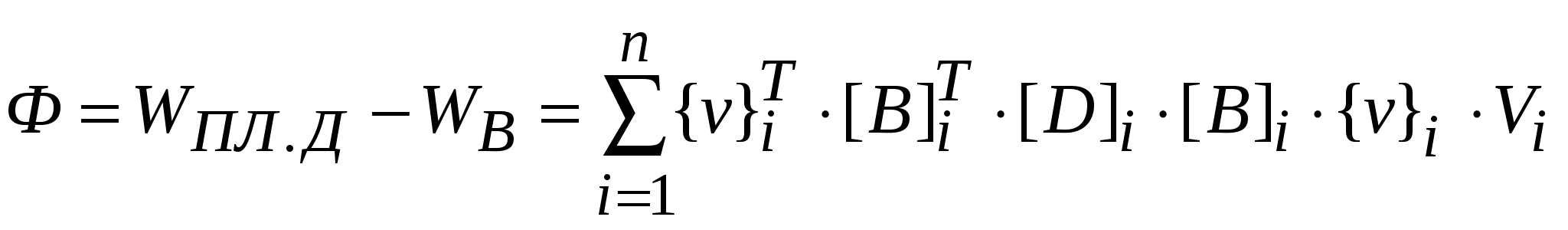 , (5) , (5)
Как видно из (5) значение функционала зависит от {v}i узловых скоростей.
Выясним, при каких скоростях узлов функционал будет принимать минимальное значения близкое к нулю.
Для этого возьмем производные от функционала по всем узловым скоростям сетки элементов и приравняем их нулю. Решив полученную систему уравнений, найдем скорости.
Если j-ый узел является граничным, нагружаемым силой, то производная будет иметь вид,
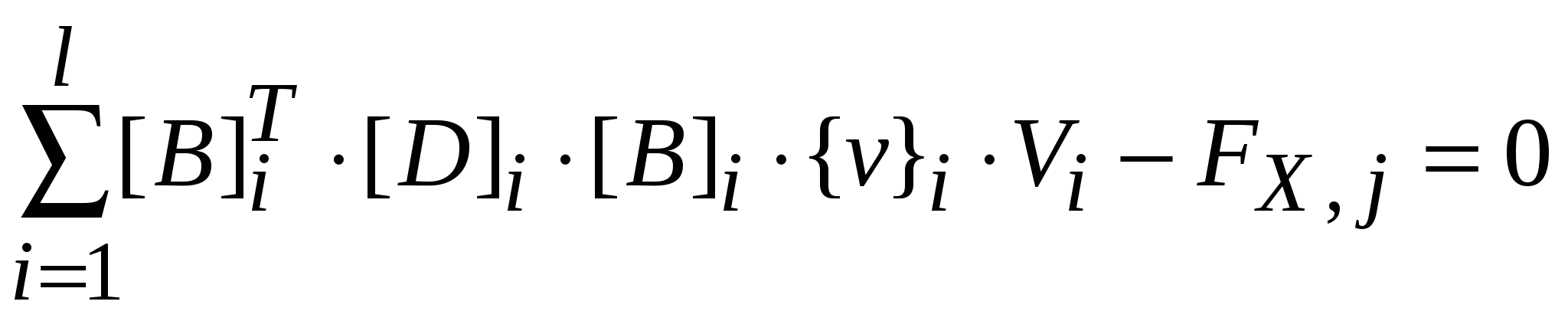 , ,
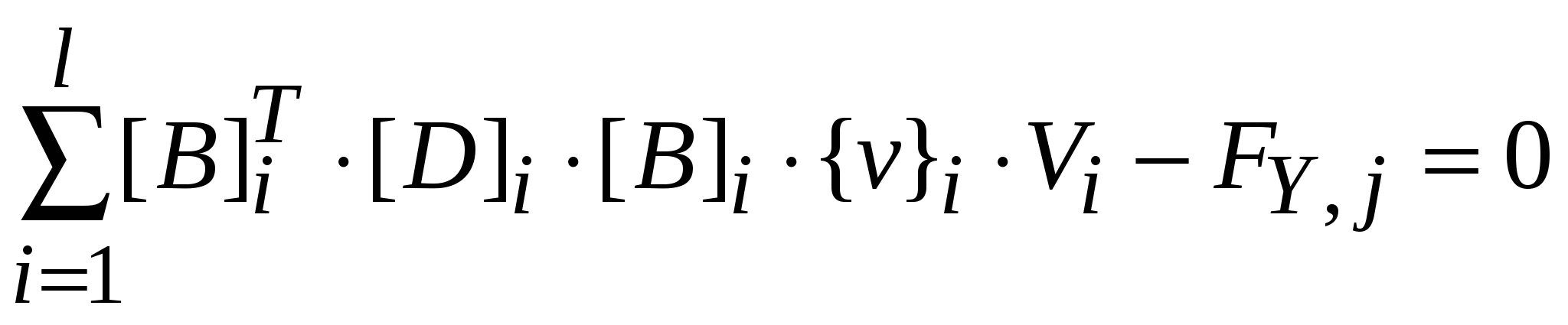 , ,
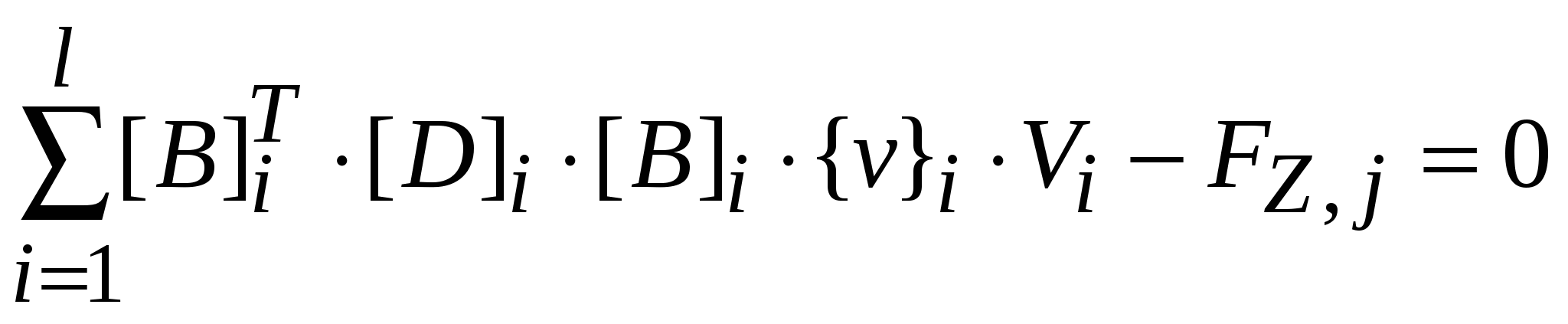 , ,
где l- количество элементов окружающих узел.
Если узел внутренний, то производная будет иметь вид:
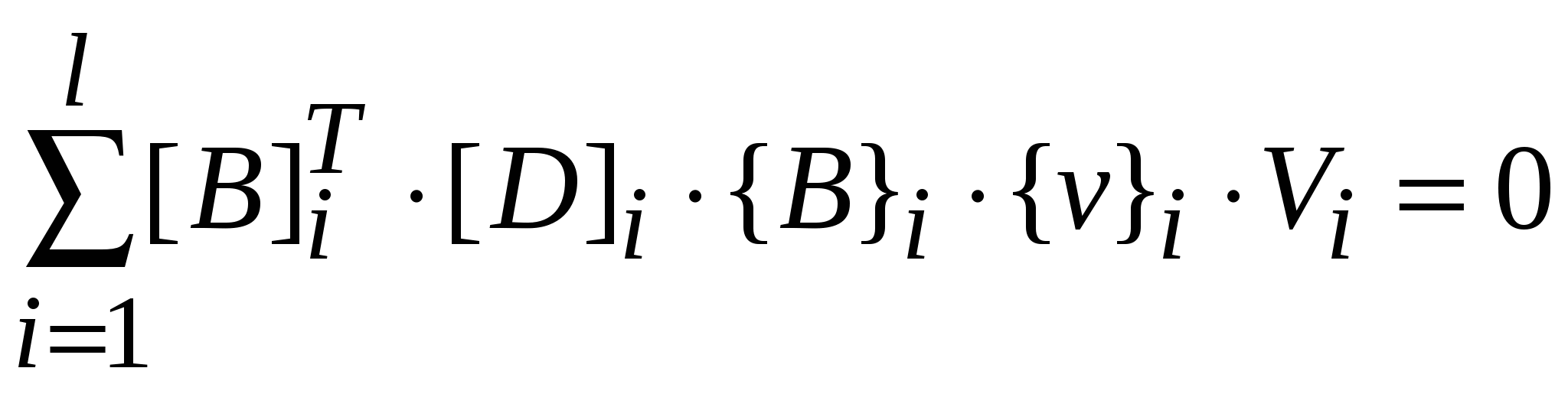
Введем обозначение:
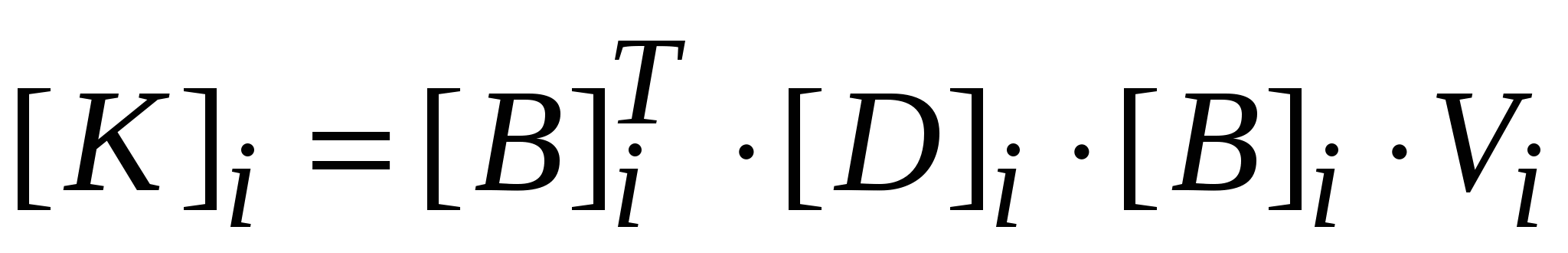 , тогда , тогда
производные примут вид:
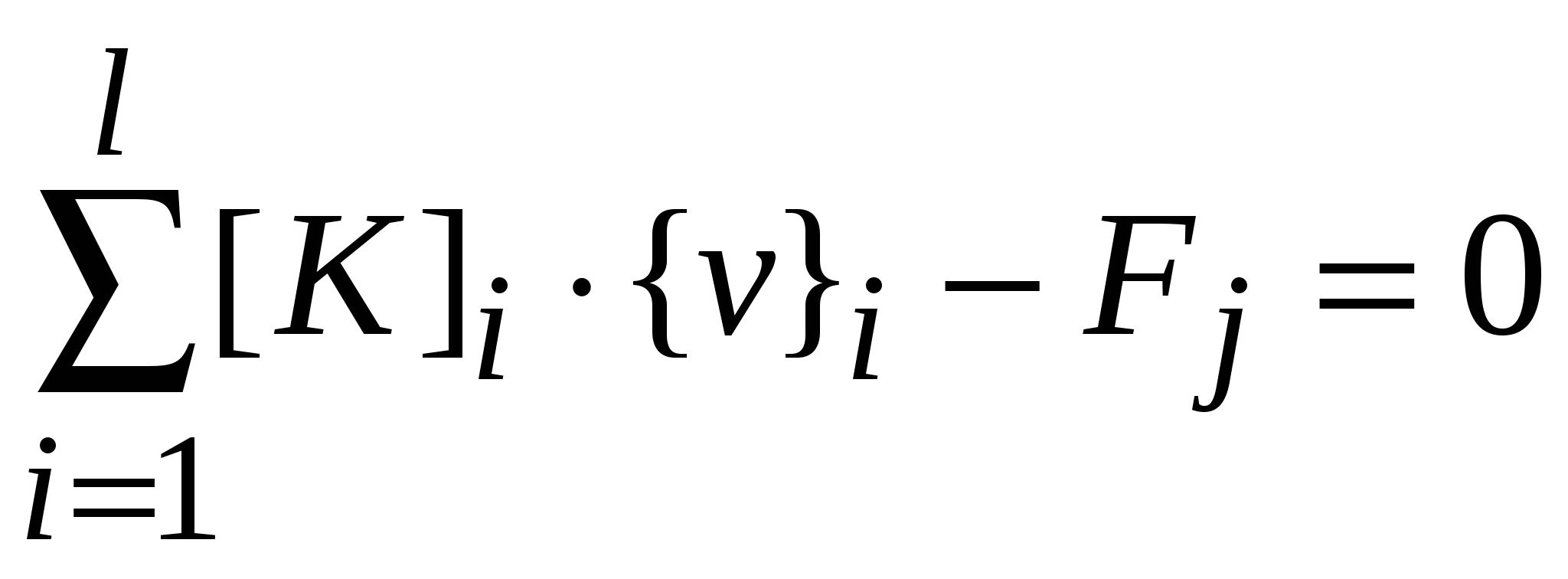 , ,
или (6)
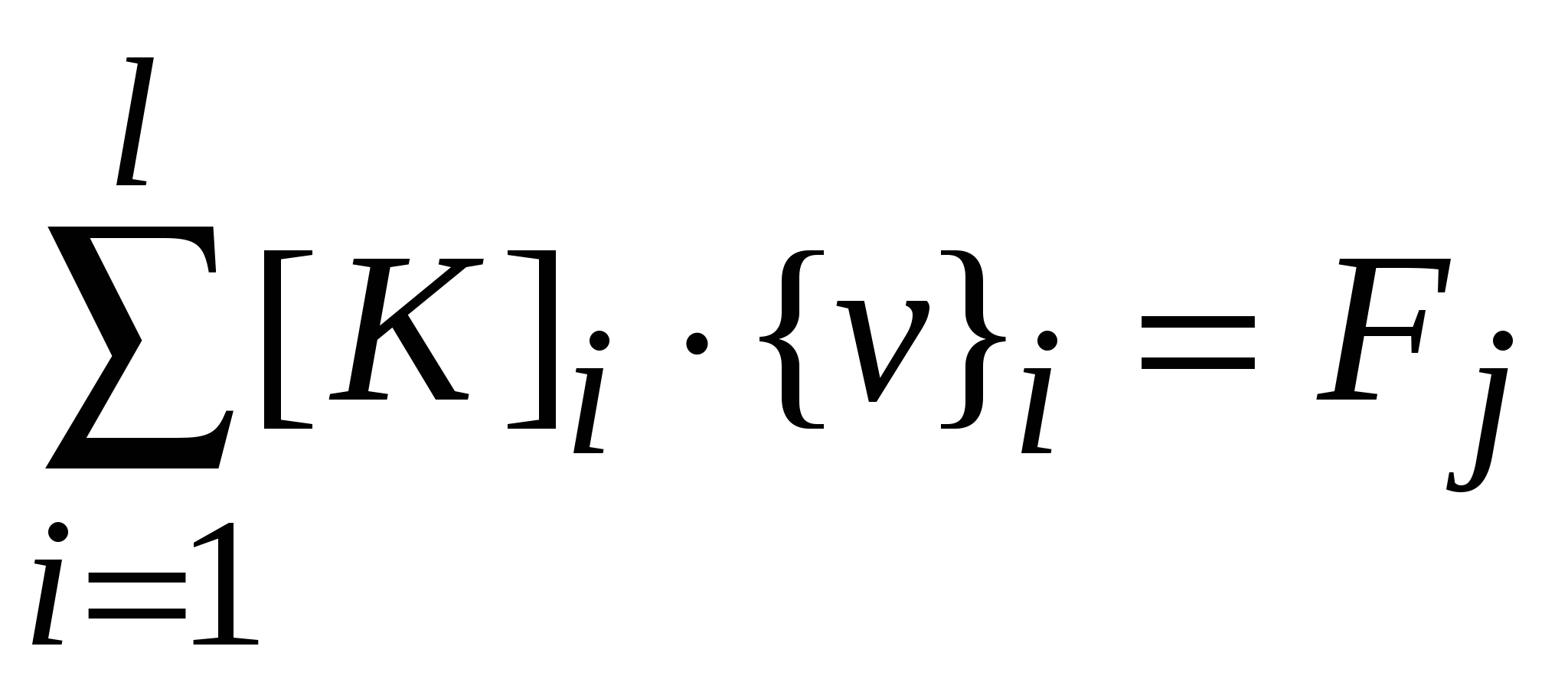
Очевидно, что произведение 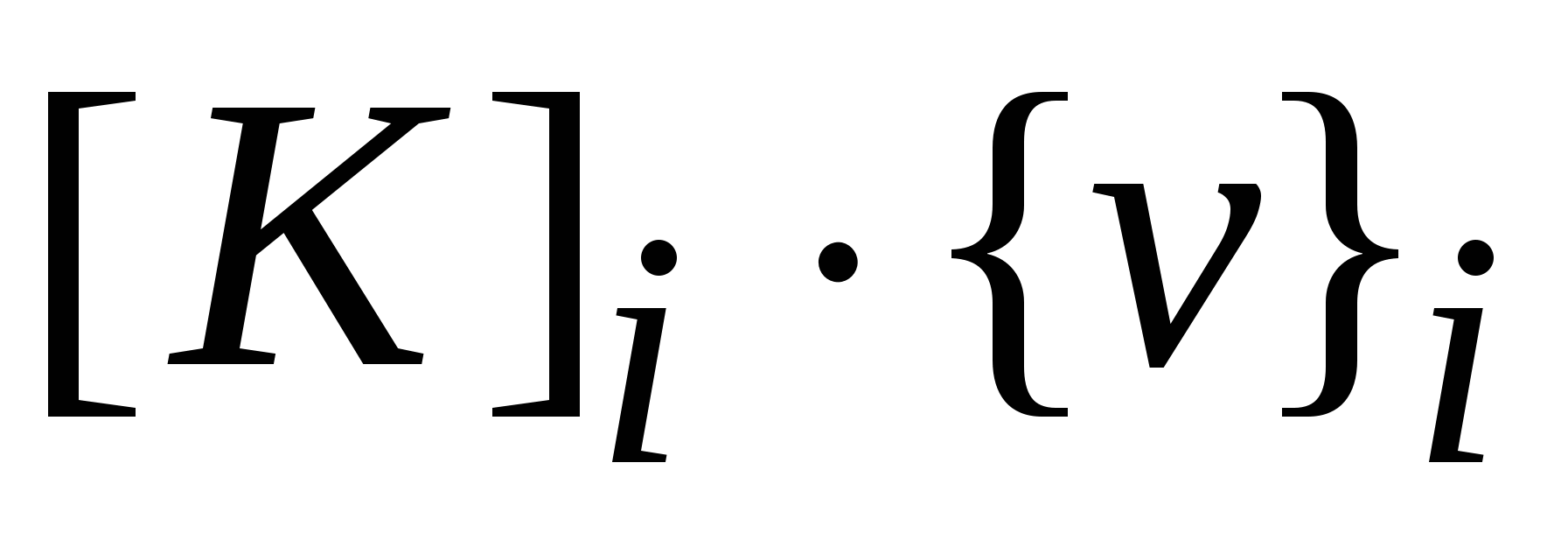 представляет собой матрицу столбец внутренних сил приложенных как бы со стороны i-го элемента к узлам, составляющим i-ый элемент. представляет собой матрицу столбец внутренних сил приложенных как бы со стороны i-го элемента к узлам, составляющим i-ый элемент.
Для плоского треугольного элемента данная матрица столбец имеет шесть компонент (рис.1).
Рисунок 1.
На j-ый узел из системы сил матрицы действуют только две со стороны i-го элемента (Fy,j и Fy,j).
Таким образом левая часть уравнения равновесия (6) представляет собой сумму внутренних сил действующих на j-ый узел со стороны окружающих элементов (сил действующих только вдоль одной оси координат).
Т.е. из шести сил каждого из L элементов окружающих j-ый узел, в сумме-левой части уравнения (6) участвует только одна – соответствующая оси координат и j-му узлу.
Уравнение (6) можно записать иначе:
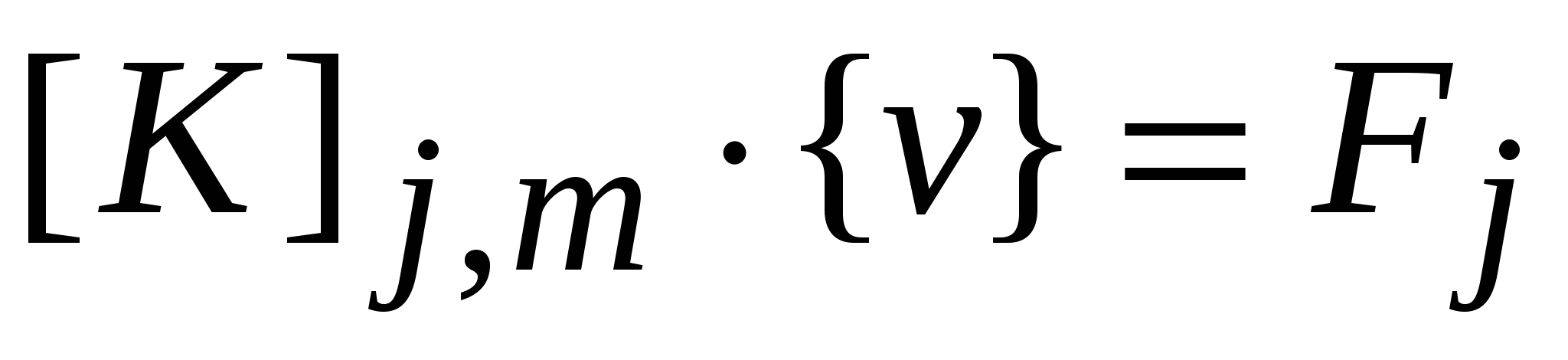 , (7) , (7)
где, 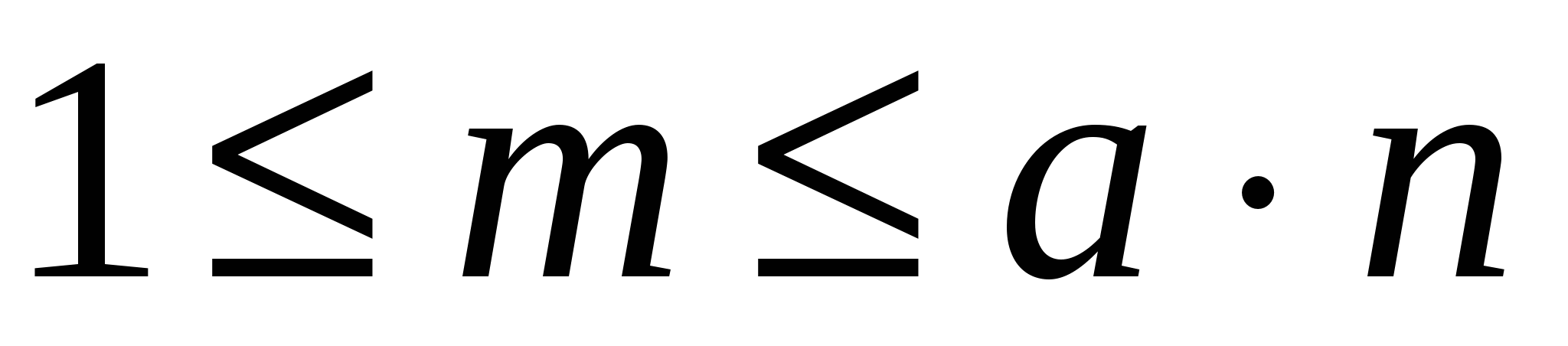 , ,
a-размерность задачи; n-количество узлов.
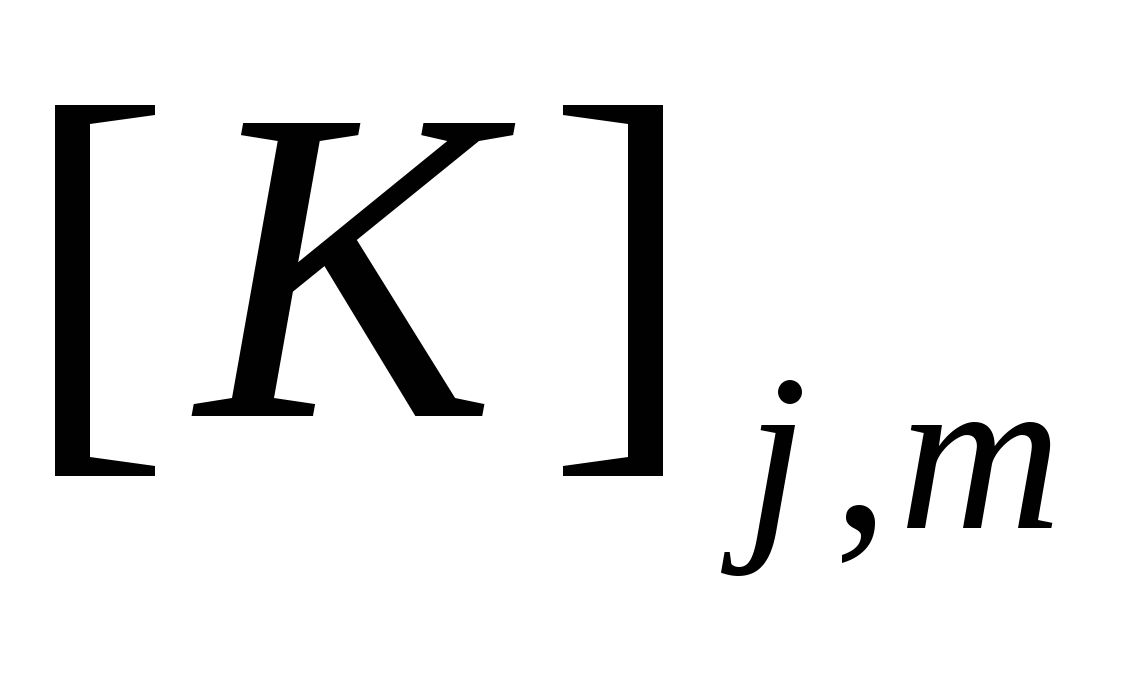 - строка коэффициентов уравнения равновесия для j-го узла вдоль соответствующей оси. - строка коэффициентов уравнения равновесия для j-го узла вдоль соответствующей оси.
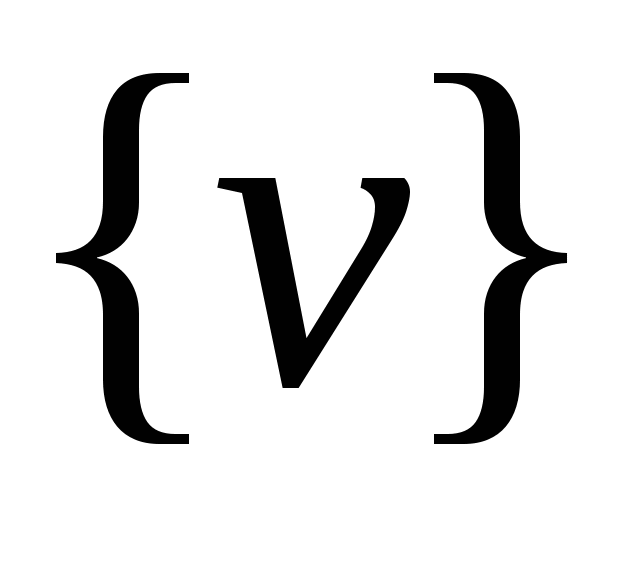 - матрица столбец узловых скоростей сетки конечных элементов. - матрица столбец узловых скоростей сетки конечных элементов.
Всю систему уравнений можно представить в виде:
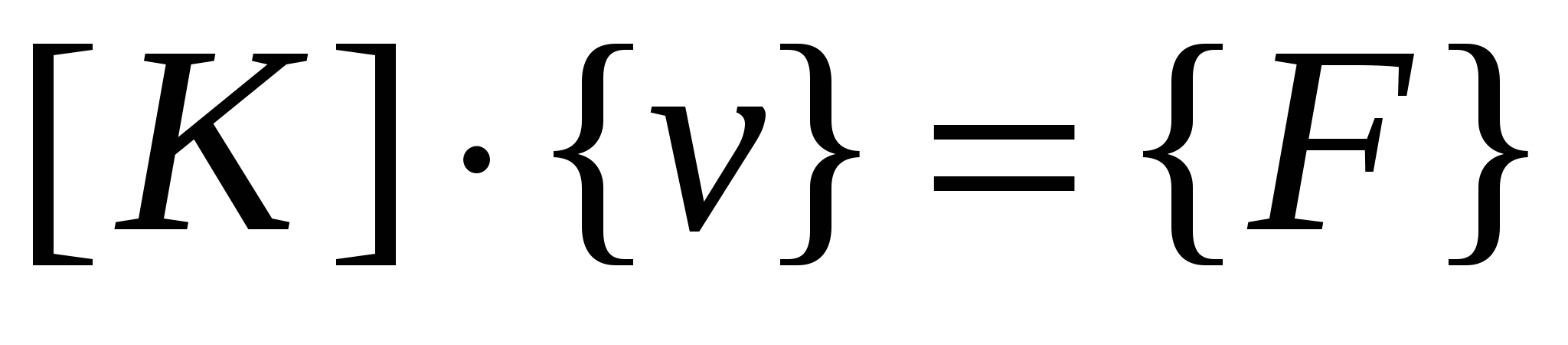 , ,
Ненулевые компоненты матрицы [K] получают присвоением или сложением соответствующих компонент матриц жесткости элементов[K]i ,
способом объединения по узлам или по элементам.
2. В случае использования модели материала(металла) с пропорциональностью девиатора напряжений девиатору скоростей деформации (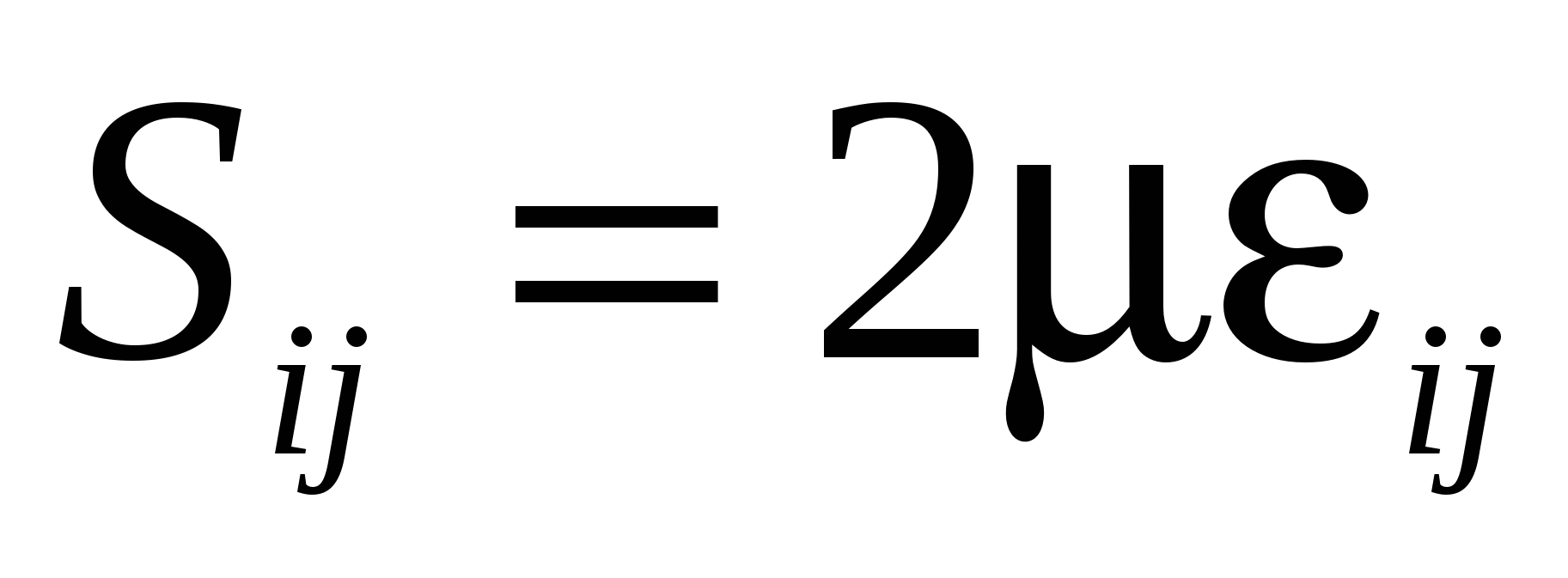 ) и сжимаемой по по закону Гука: ) и сжимаемой по по закону Гука:
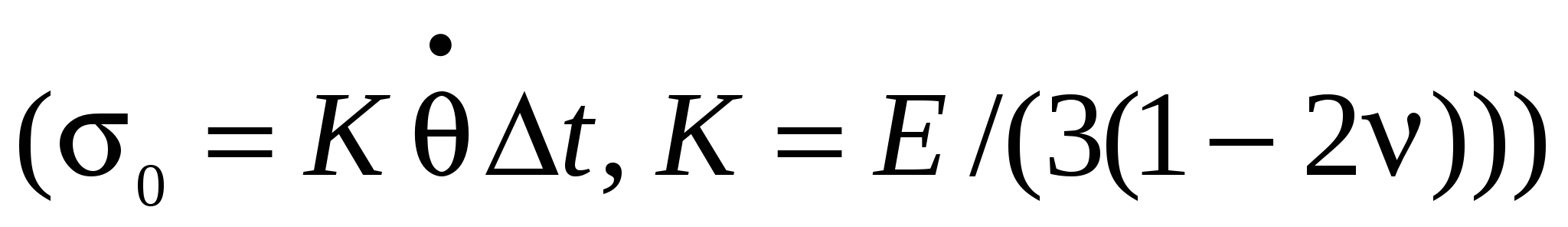 , ,
где,  - объёмная скорость деформации, - объёмная скорость деформации,
 - интервал времени – время, принятое для одного шага нагружения модели. - интервал времени – время, принятое для одного шага нагружения модели.
Уравнение связи имеет вид:
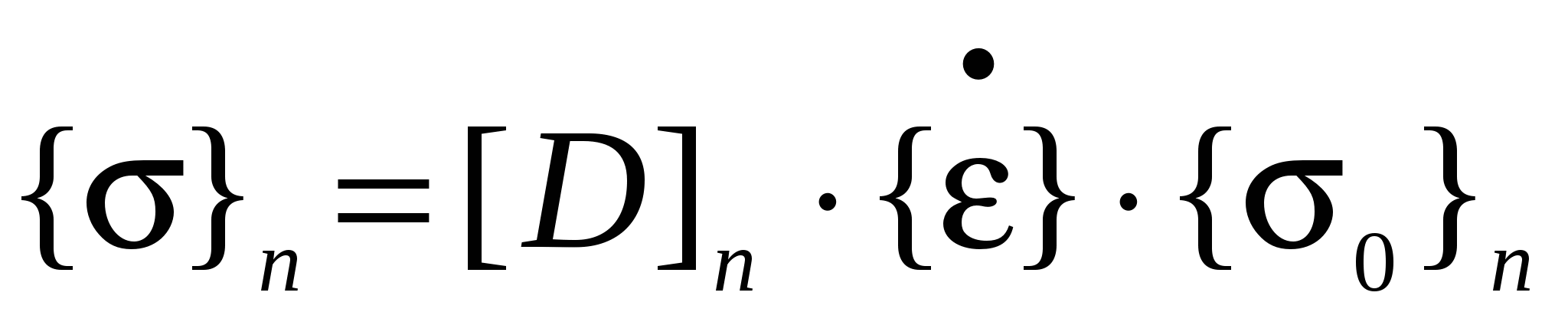 , ,
где, 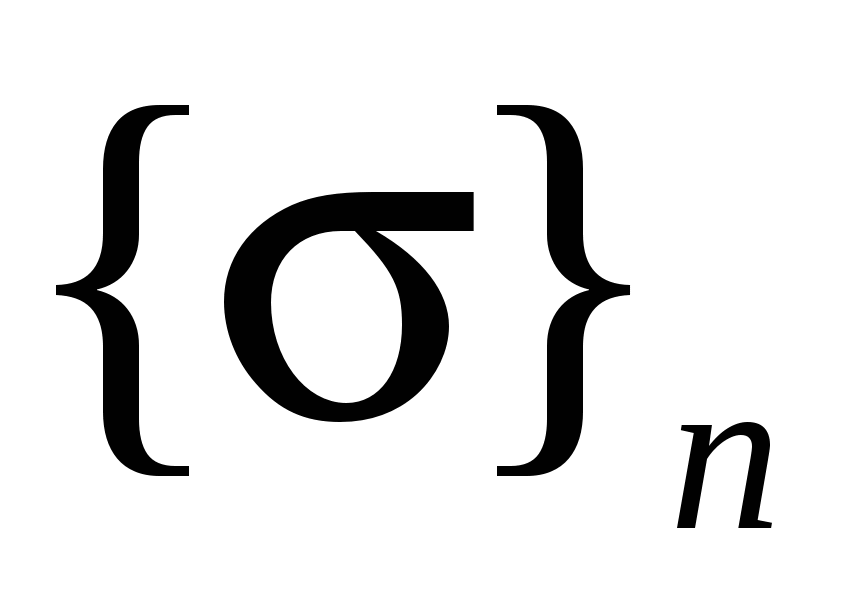 -матрица столбец напряжений n-го элемента, -матрица столбец напряжений n-го элемента,
[D]n – матрица упруговязкости,
 - матрица столбец скоростей деформации n-го элемента, - матрица столбец скоростей деформации n-го элемента,
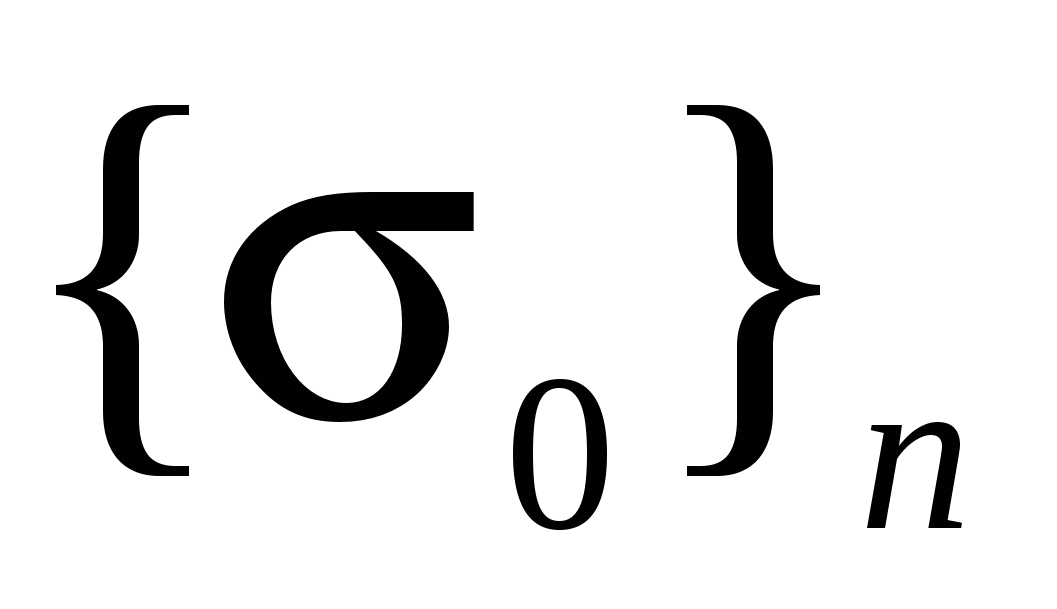 -матрица столбец гидростатического давления накопленного элементом за предыдущие этапы нагружения. -матрица столбец гидростатического давления накопленного элементом за предыдущие этапы нагружения.
Матрицы [D]n и { o}n для плоскодеформированного состояния имеют вид: o}n для плоскодеформированного состояния имеют вид:
 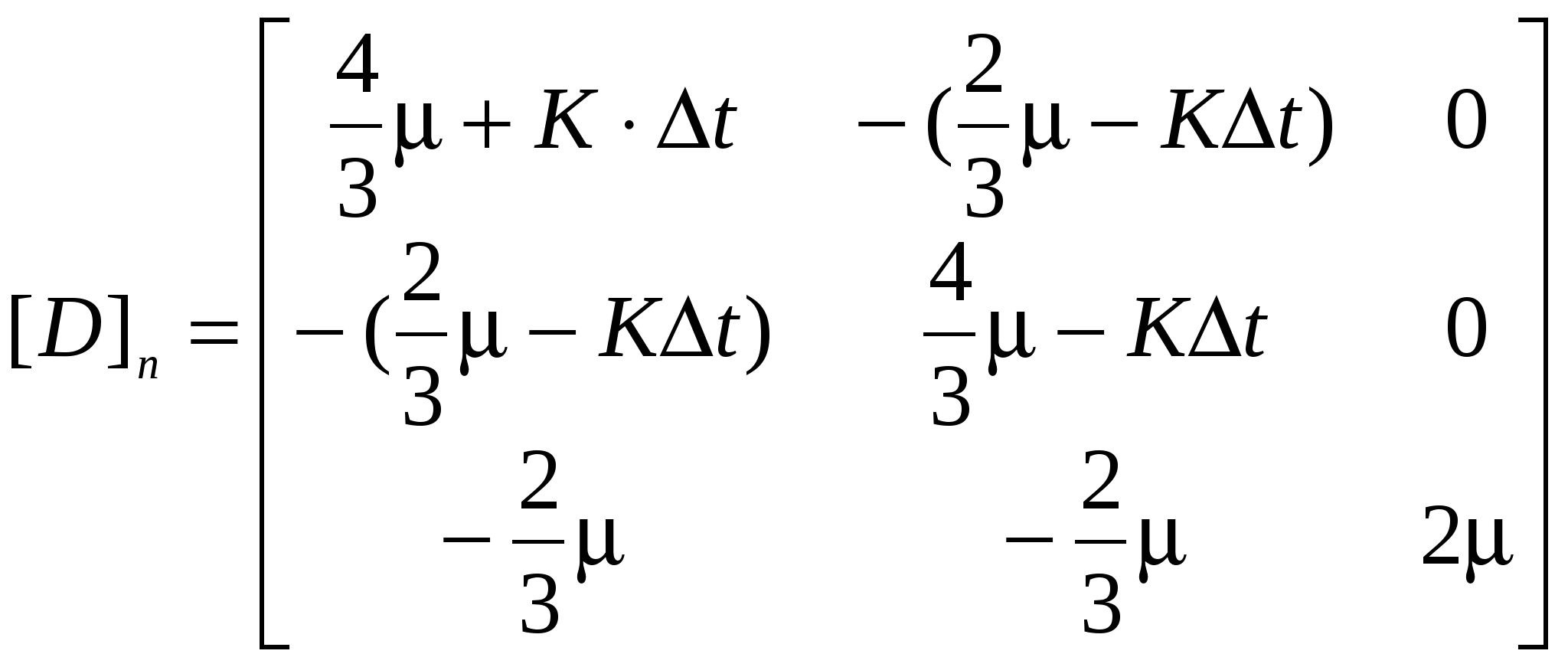 , ,
где, 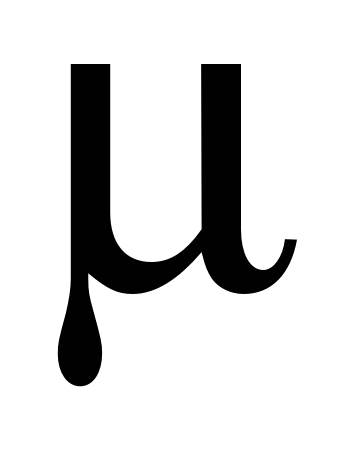 - коэффициент вязкости, - коэффициент вязкости,
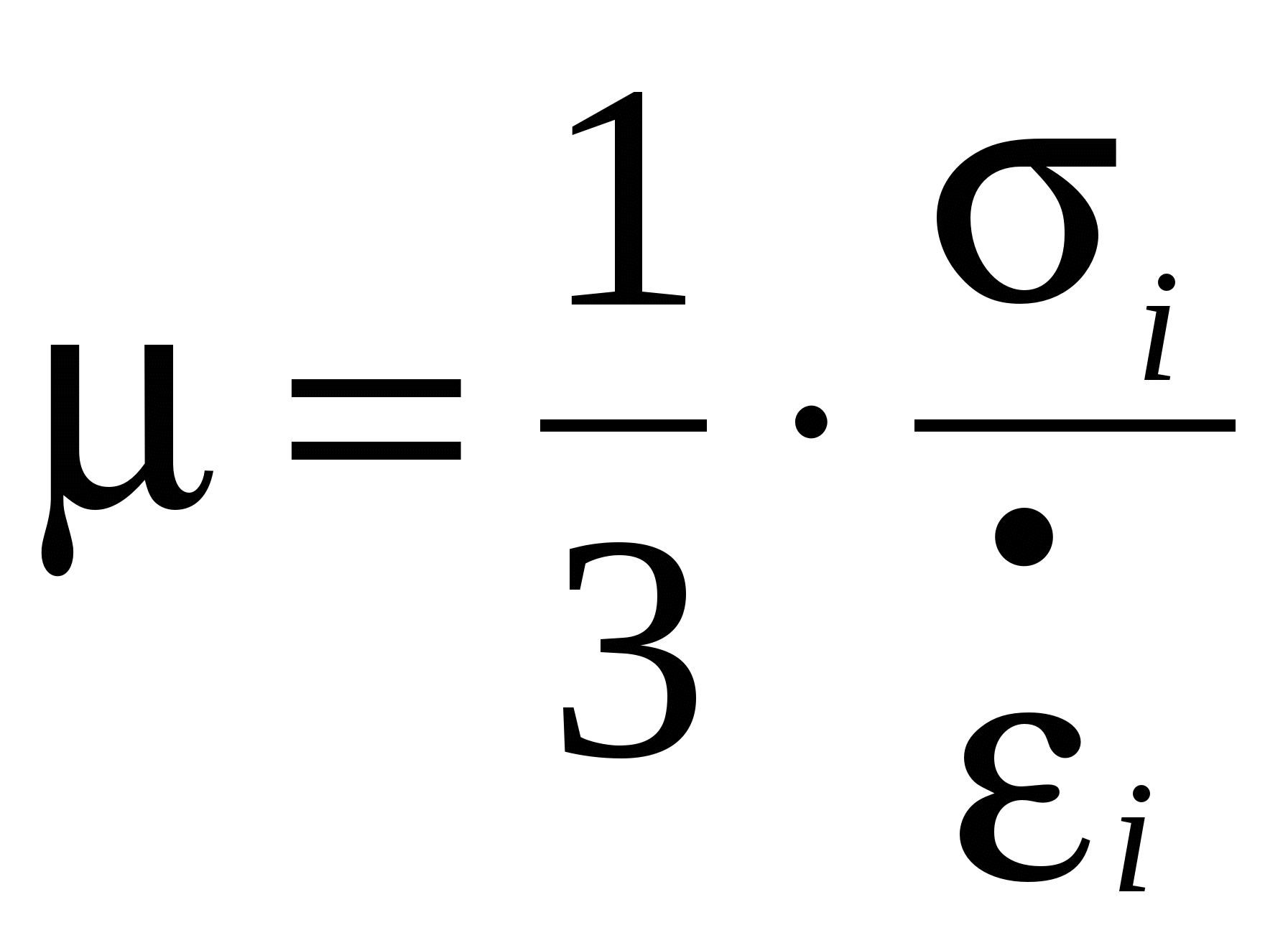 , ,
где, 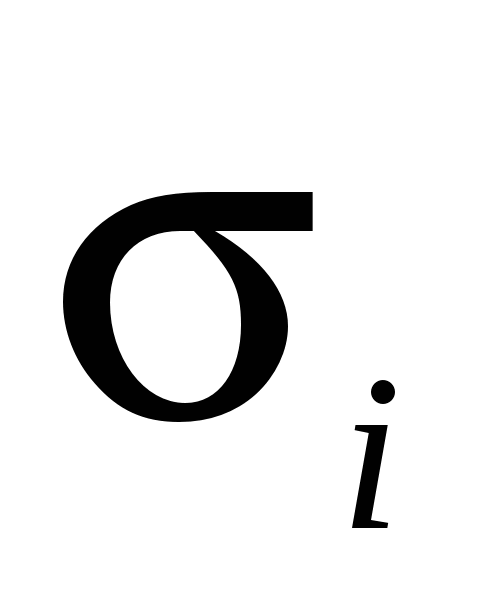 - интенсивность напряжений рассчитывается с учетом интенсивности скоростей деформации - интенсивность напряжений рассчитывается с учетом интенсивности скоростей деформации 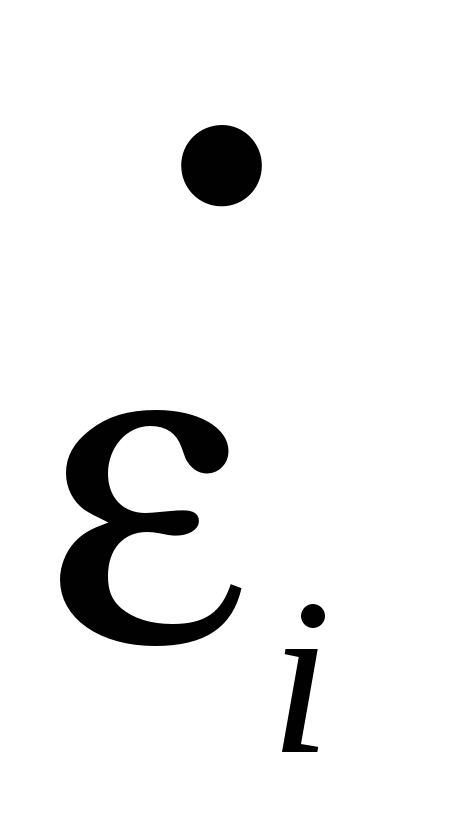 , по диаграмме скоростного упрочнения металла , по диаграмме скоростного упрочнения металла 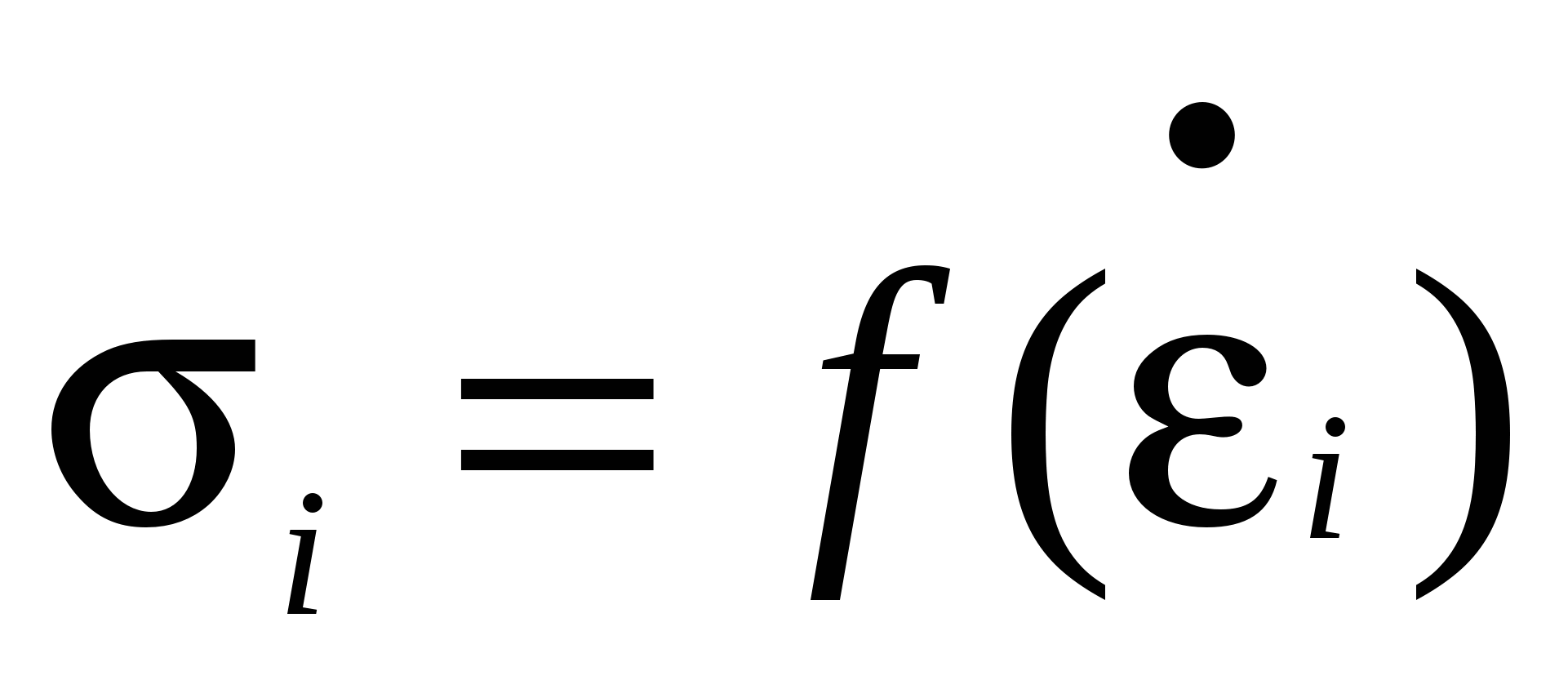 , ,
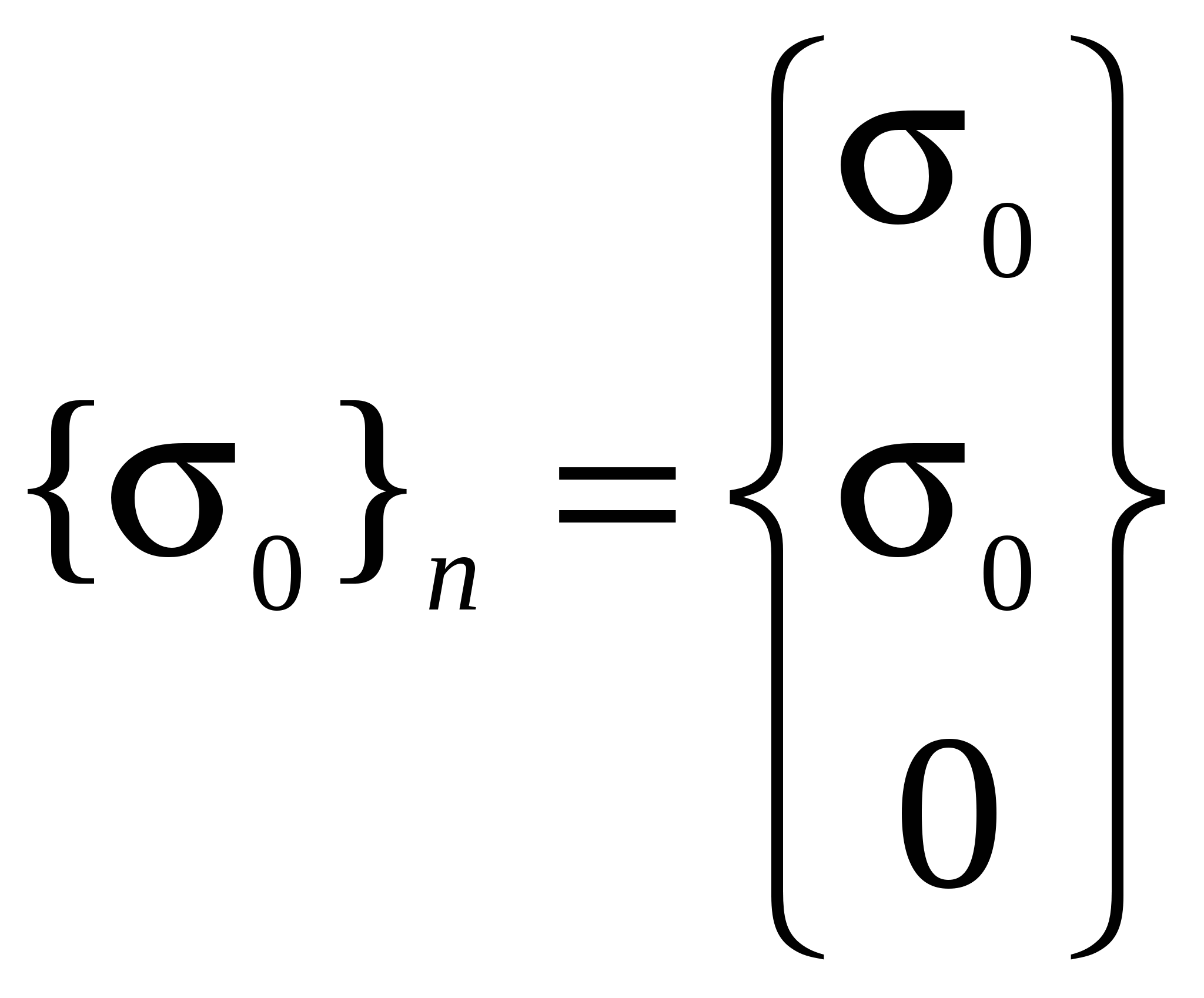 , ,
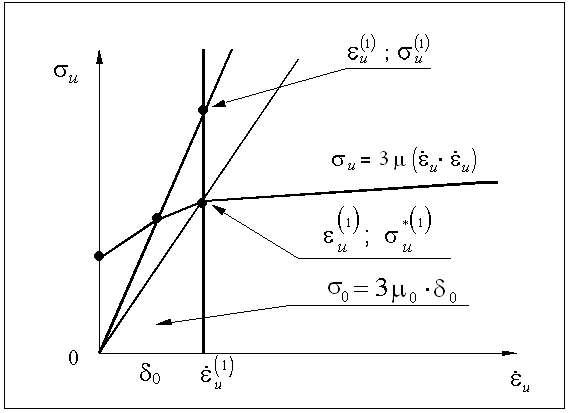
На первом шаге нагружения конечно-элементной модели для всех элементов принимается: 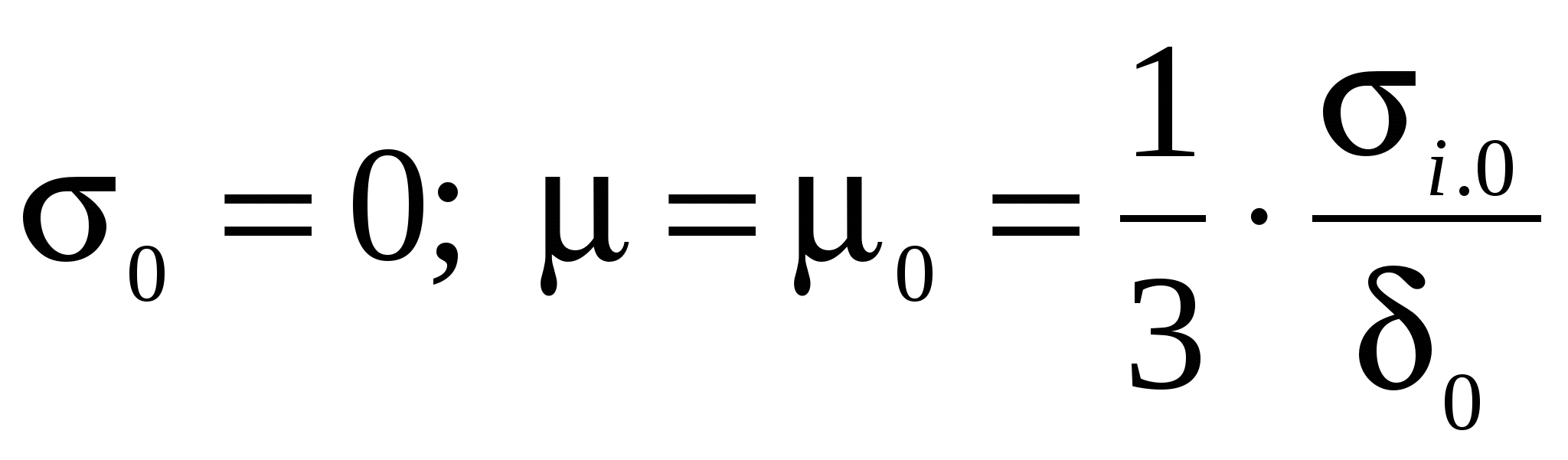 (см. рис.2). (см. рис.2).
|
|
|
 Скачать 3.24 Mb.
Скачать 3.24 Mb.