Решение Вычислим какое количество времени занимает передача файла по каналу связи без архивации
 Скачать 1.16 Mb. Скачать 1.16 Mb.
|
|
Задача 10. Вычисление циклического контрольного кода В основе теории вычисления циклического контрольного кода лежит понятие полинома или, как его еще называют, многочлена. Полином (А(х))- это формально заданный степенной ряд, т.е. сумма множества степенных выражений независимых переменных. Например, 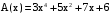 Степенью полинома называют число r равное максимальному показателю степени полинома. Для приведенного примера r = 4. Формальная запись примера должна выглядеть: 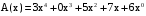 В общем случае, любой блок информации в памяти компьютера можно считать полиномом, если рассматривать в качестве переменной x один бит. CRC коды построены на рассмотрении битовой строки как строки коэффициентов полинома. k-битовая строка - коэффициенты полинома степени k -1. Самый левый бит строки - коэффициент при старшей степени. Например, строка 110001 представляет полином 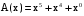 Для вычисления контрольного кода понадобится еще один полином, называемый порождающим полиномом G(x). Порождающий полином – это полином который должен удовлетворять следующим свойствам: должен быть неприводимым; должен быть делителем двучлена xn+1; степень полинома р должна быть настолько большой, чтобы количество остатков 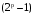 было не меньше количества ошибок, которые требуется локализовать. было не меньше количества ошибок, которые требуется локализовать.Для получения контрольного кода информационный полином A(x) умножается на 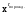 (к исходному полиному добавляются нулевые биты в количестве r порождающего, т.е. осуществляется сдвиг на r разрядов влево), а затем делится на порождающий полином G(x). Частное – полином Q(x) – отбрасывается (не участвует в дальнейших вычислениях). (к исходному полиному добавляются нулевые биты в количестве r порождающего, т.е. осуществляется сдвиг на r разрядов влево), а затем делится на порождающий полином G(x). Частное – полином Q(x) – отбрасывается (не участвует в дальнейших вычислениях).Остаток от деления R(x) и является контрольным кодом, хранящимся для последующих проверок. Между полиномами, таким образом, справедливо следующее соотношение A(x) = Q(x) * G(x) + R(x) 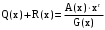 Исходя из этой формулы, вычисление контрольного числа сводится к организации умножения и деления числа произвольной разрядности. Умножение информационного полинома на х реализуется тривиально - как дописывание после младшего разряда полинома r нулевых разрядов. Пример. Предположим, что контролируются данные вида A(x)=11010011, которым соответствует полином 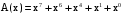 . В качестве порождающего полинома выбран полином число G(x)=1001, которому соответствует . В качестве порождающего полинома выбран полином число G(x)=1001, которому соответствует 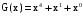 (r=4), следовательно контрольный код будет получен делением Полинома A(x)=110100110000 на G(x)=10011. (r=4), следовательно контрольный код будет получен делением Полинома A(x)=110100110000 на G(x)=10011.Для организации деления можно реализовать специальный алгоритм : r+1 старших разрядов информационного полинома складываются по модулю 2 с порождающим полиномом и в частное заносится 1. В дальнейшем, полином, полученный после сложения информационного полинома с порождающим полиномом, будем называть остатком информационного полинома. После сложения самый старший разряд остатка информационного полинома равен 0, поэтому сдвигаемся на один разряд вправо. Если следующий разряд остатка полинома равен нулю, то в частное заносится 0 и сдвигаемся дальше, в противном случае снова производится сложение по модулю 2 группы разрядов длиной r+1 остатка информационного полинома с порождающим полиномом. Последнее действие повторяется до тех пор, пока степень остатка не станет меньше степени порождающего полинома. Полученный остаток и будет являться контрольным кодом. Замечание 1. Поскольку нас интересует только контрольный код - остаток от деления, частное вычислять не надо. Замечание 2. Полиномиальная арифметика выполняется по модулю 2. Сложение и вычитание происходит без переноса разрядов. Так что обе эти операции эквивалентны операции XOR (eXclusive OR). Деление выполняется как обычно в двоичной системе счисления с той лишь разницей, что вычитание выполняется по модулю 2. Часто вычисления в соответствии с этими правилами называют CRC-арифметикой. Пример вычисления 110100110000 | 10011 10011 11000111 10010110000 10011 1110000 10011 111100 10011 11010 10011 1001 - остаток от деления, т.е. R(x) Очевидно, что число разрядов полинома R(x) определяется разрядностью порождающего полинома G(x). Из теории следует, чем больше величина R(x), тем больше способность контрольного кода обнаруживать ошибки при передачи данных. В дальнейшем осуществляется передача исходного полинома A(x) к которому добавляется остаток от деления R(x) 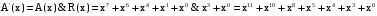 При получении данного полинома, выделяются последние биты, которые соответствуют количеству бит в контрольной сумме и полученный полином делится на них, если передача произошла без ошибок, то R(x)=0, т.е. остатка от деления нет. ГОСТ 28082—89 «Методы обнаружения ошибок при последовательной передаче данных» устанавливает в качестве основного порождающий полином 16-й степени 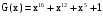 (1 0001 0000 0010 0001). Для более высокой степени помехозащищенности передаваемой информации ГОСТом рекомендовано использовать полином 32-й степени (1 0001 0000 0010 0001). Для более высокой степени помехозащищенности передаваемой информации ГОСТом рекомендовано использовать полином 32-й степени 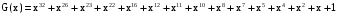 (1 0000 0100 1100 0001 0001 1101 1011 0111). Международные стандарты предлагают использовать следующие порождающие полиномы для циклического кодирования: 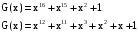 Задание: Вычислить CRC для строки кода задания 8 в соответствии со своим вариантом для порождающих полиномов: 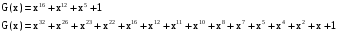 Провести проверку. Таблица порождающих полиномов 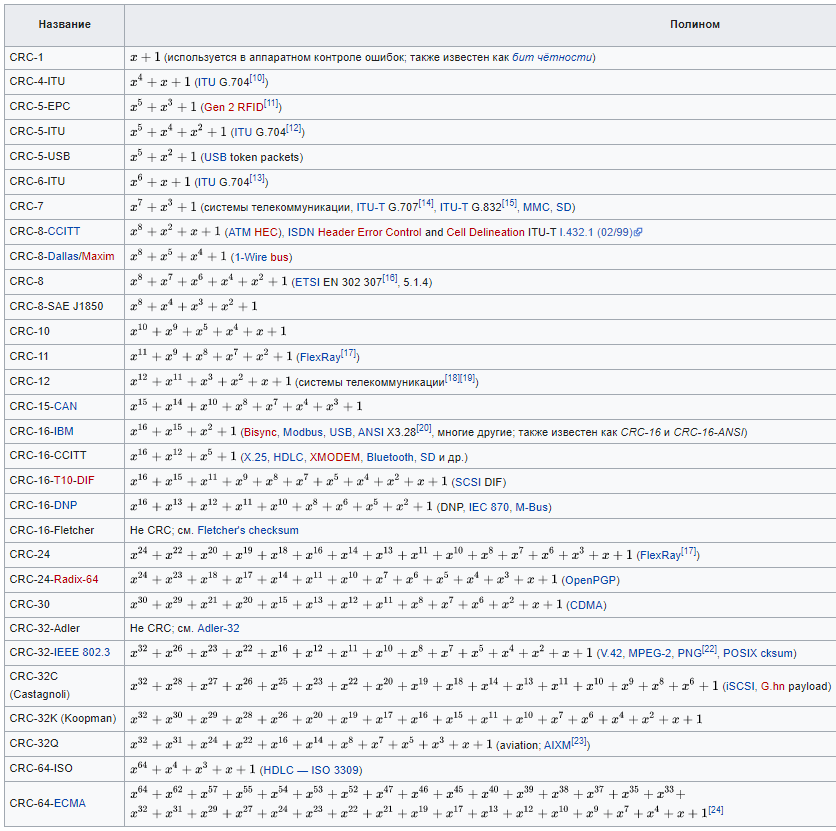 Таблица 11. Исходные данные для решения Задачи 8
Задача 11 К основным параметрам циклических кодов относятся: n – длина кода; k – количество информационных символов; dH – минимальное Хэмминговое расстояние между кодовыми комбинациями. t – количество ошибок в кодовой комбинации, которые могут быть исправлены при декодировании этих кодов. В таблице указаны параметры основных кодов: Хэмминга, Боуза-Чоудухри-Хоквингема (БЧХ), Рида-Соломона (РС), Рида-Маллера (РМ).  Параметр m может принимать любые целые числа. Обычно m <= 10, длина циклического кода n<=1000. Кодовая скорость определяется параметром 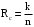 Коды, позволяющие обнаруживать и даже исправлять ошибки, называются помехоустойчивыми или корректирующими. Помехоустойчивые коды всегда являются избыточными. Кодовая комбинация такого кода включает в себя информационную последовательность (k бит) и проверочную часть (r бит), код является блочным и разделимым. В старших разрядах кодовой комбинации длиной n=k+r размещаются биты информационной последовательности, в младших разрядах – биты проверочной части. В реально используемых циклических кодах вносимая избыточность R=r/n составляет не более 5%. Кодовые слова кода (или разрешенные кодовые комбинации) отличаются друг от друга в некотором числе разрядов, которое называется расстоянием Хемминга (d), в зависимости от сравниваемой пары комбинаций расстояние Хемминга может меняться, но не может быть меньше некоторого минимального значения dmin , которое называется кодовым расстоянием. Кодовое расстояние кода – это важнейшая характеристика, которая полностью определяет способность кода обнаруживать и исправлять ошибки. Формулы, выражающие связь между кодовым расстоянием и весом комбинаций ошибок, которые гарантированно обнаруживаются или исправляются, обычно записываются в виде: 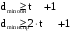 Запись означает, что, к примеру, код с кодовым расстоянием равным 3 гарантированно обнаруживает любые комбинации одиночных и двойных ошибок, комбинации ошибок большей кратности обнаруживает частично, код может исправлять только одиночные ошибки. Мы рассматриваем передачу двоичных комбинаций длиной n символов. Комбинация ошибок также имеет длину n и имеет единицы только на позициях, соответствующих неправильно принятым символам. Число единиц в комбинации ошибок t называют весом или кратностью. Искаженная комбинация на входе декодера циклического кода в приемнике представляет собой поразрядную сумму по модулю 2 переданной кодовой комбинации кода и возникшей комбинации ошибок. Процедура декодирования принятой комбинации (возможно искаженной) сводится к проверке соотношения: принятые проверочные элементы кодовой комбинации совпадают с результатом вычисления этих элементов принимающей стороной? Для проверки этого соотношения декодер вычисляет синдром принятой последовательности. Синдром S – это строка, которая содержит r=n-k элементов. Для циклических кодов синдром вычисляется в соответствии с процедурой, рассмотренной ниже. Вид синдрома для заданного кода зависит исключительно от вида комбинации ошибки. Задание. Система передачи данных использует циклический код с параметрами (n,k) и пораждающий полиномом g(x), который соответствует определенному простому числу На вход кодера канала поступает информационная последовательность u. Система передачи данных использует циклический код с параметрами (7,4) и порождающий полиномом заданный числом 11. На вход кодера канала поступает информационная последовательность u=1001 Построить образующий полином Запишите порождающий матрицу G заданного кода в каноническом виде. Определите кодовое расстояние кода d0 (dmin). Выделить все синдромы, соответствующие одиночным ошибкам. Определите кодовую комбинацию v на выходе кодера. Внесите 1-кратную ошибку (t=1) в любые разряды комбинации v. Определите синдром s комбинации с ошибкой. Порождающая матрица строится из порождающего полинома. Основное свойство порождающего полином – он делится только на себя и на единицу, следовательно является простым числом. Исходный полином который соответствует числу 11 есть: g(x)=x3+x+1, можно представить в виде двоичного числа g(x) = 1011 1011дв = 11дс. Так как код с параметрами С(7,4), значит порождающая матрица состоит из 4 строк и семи столбцов Отсюда следует, что по синдрому s(x) можно однозначно определить вектор ошибки е(х). Прежде чем строить порождающую матрицу вычислим все синдромы S. Синдром вычисляется как остаток от деления полинома вида A(x)=100(0) (вектор ошибки) на порождающий полином, деление производится до тех пор, пока синдромы не начнут повторяться. Разделим полином вида A(x)=100(0) на порождающий полином g(x)= 1011  Составим соответствие полинома ошибки e и полинома синдрома для k равное 2p-1, где p – максимальная степень порождающего полинома.
Исходя из этого запишем получившуюся порождающую матрицу G(x)=G(7,4)
Прохождение сообщения через кодек математически выглядит как V(x)=U(x)*G(x) 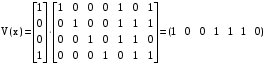 При умножении вектора на матрицу исходим из правила 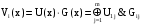 где m – число строк в матрице и векторе, должны быть одинаковы & - операция конъюнкции, логическое умножение 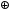 - сложение по модулю два. - сложение по модулю два.Проведем проверку путем деления в двоичном виде: Делимое (7 разрядов) Делитель (4 разряда)
Так же проверить можно умножив полученный вектор на проверочную матрицу Из порождающей матрицы G(x) выделяем подматрицу синдромов S(x) 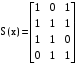 В данною матрицу синдромов добавляем единичную подматрицу вида 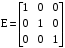 Получаем проверочную матрицу H(x) 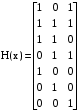 Умножим полученный вектор на проверочную матрицу e(x)=V(x)*H(x) 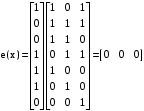 Если S=0, значит ошибки в принятой комбинации отсутствуют. По заданию при передаче по дискретному каналу возникла комбинация ошибок весом t=1. в любом разряде. При наличии в принятой последовательности одной ошибки вектор синдрома s будет иметь по крайней мере один ненулевой элемент. Пусть ошибка произошла в шестом разряде и на вход декодера поступила комбинация e=1001100, умножим данную последовательность на проверочную матрицу 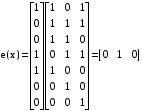 Как видно результирующая последовательность не равна [0 0 0], следовательно в полученной комбинации присутствует ошибка.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
