Решение Вычислим какое количество времени занимает передача файла по каналу связи без архивации
 Скачать 1.16 Mb. Скачать 1.16 Mb.
|
|
Задача 12 Пример По каналу связи передаются сообщения, вероятности которых равны: p(x1) = 0,95; p(x2) = 0,96; p(x3) = 0,97; p(x4) = 0,98; Длина передаваемого сообщения равна 500 символов. Время передачи одного двоичного символа производится за время t=10-5 с. Производится передача 4 сообщений, m=4. Определить: Энтропию источника информации H(X). Безусловную энтропию приемника информации H (Y). Общую условную энтропию H (Y/X). Скорость передачи информации. Потери информации в канале связи при передаче 500 символов алфавита. Среднее количество принятой информации. Пропускную способность канала связи. Решение На первом этапе нам надо построить канальную матрицу, которая определяет потери информации в канале связи. Канальную матрицу будем строить по следующему принципу. Значения элементов, которые располагаются по диагонали (левый верх – правый низ) равны вероятностям того, что сообщение было передано и является ошибочным исходя из передачи четырех последовательных сообщений. Остальные члены матрицы рассчитываются из распределения вероятности ошибочной передачи, с учетом уже переданного сообщения. Построим матрицу, определяющую потери информации в канале связи для нашего примера. Вероятность ошибочной передачи определяется по формуле: 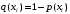 (36) (36)Соответственно: q(x1) = 0,05; q(x2) = 0,04; q(x3) = 0,03; q(x4) = 0,02; Исходя из того, что сообщения передаются друг за другом и связаны между собой, то найдем вероятность ошибки, исходя из того, что Q(X)=1: 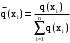 (37) (37)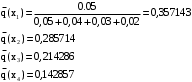 Найдем полную вероятность события ошибочной передачи: 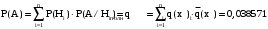 Найдем условную вероятность ошибочной передачи каждого сообщения, которые будут определять диагонали матрицы: 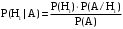 (38) (38)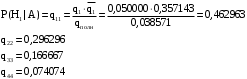 Тогда P(Y/X) выглядит как: 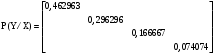 Заполним недостающие элементы матрицы согласно формуле: 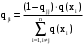 (39) (39)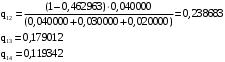 Таким образом, канальная матрица потери сообщения в канале связи выглядит следующим образом: 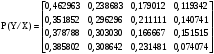 Энтропия источника сообщений: 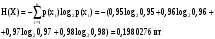 Вероятности появления символов на входе приемника рассчитываются по формуле полной вероятности:  Рассчитаем энтропию приемника: 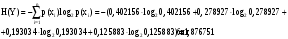 Общая условная энтропия: 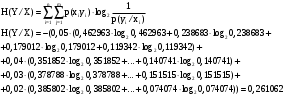 Скорость передачи информации: 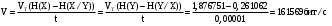 Потери информации в канале связи: 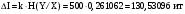 Среднее количество принятой информации: 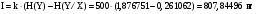 Пропускная способность канала связи 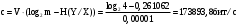 Исходные данные для решения Задачи 12 По каналу связи передаются 4 сообщения. Исходное безошибочное сообщение берется из Задачи 8 для своего варианта. Данное сообщение должно быть закодировано методом Шеннона-Фано. Исходный алфавит равен алфавиту сообщения. Таким образом получается исходное сообщение в двоичном представлении. Для исходного сообщения необходимо определить вероятности p(x1), p(x2), p(x3), p(x4). Для определения p(x1) – Первая буква А заменяется на букву О, а первая буква О заменяется на А (в двоичной кодировке). Для определения p(x2) – С учетом п. 1, первая буква М заменяется на букву Н, а первая буква Н заменяется на М (в двоичной кодировке). Для определения p(x3) – С учетом п. 2, первая буква И заменяется на букву Е, а первая буква Е заменяется на И (в двоичной кодировке). Для определения p(x4) – С учетом п. 3, первая буква П заменяется на букву Р, а первая буква Р заменяется на П (в двоичной кодировке). Время передачи одного двоичного символа составляет t=10-5 с. Производится передача 4 сообщений, m=4. Определить: Энтропию источника информации H(X). Безусловную энтропию приемника информации H (Y). Общую условную энтропию H (Y/X). Скорость передачи информации. Потери информации в канале связи при передаче 500 символов алфавита. Среднее количество принятой информации. Пропускную способность канала связи. Задание №13 Постановка задачи. В соответствии с номером варианта (таблица № 14) необходимо найти маршрут и время самого быстрого прохождения пакета от маршрутизатора с номером 1 до пользователя, который получает пакет из маршрутизатора с номером 25 (рисунок 1), применяя алгоритм Дейкстры. Условия ограничения Пакет всегда направляется от маршрутизатора с меньшим номером к маршрутизатору с большим номером. Например, с маршрутизатора 9 пакет может быть передан на маршрутизаторы 12, 13, 18, 21, 24 и не может быть передан на маршрутизатор 2. Канал связи определяет связь маршрутизатора с меньшим номером и маршрутизатора с большим номером Вес канала связи между маршрутизаторами вычисляется исходя из скорости обработки пакета в маршрутизаторе с меньшим номером. Для маршрутизатора с № 1 считается, что пакет уже поступил в маршрутизатор и находится в стадии обработки. Для маршрутизатора с № 25 необходимо учесть, что существует канал связи между маршрутизатором с № 25 и пользователем. При прохождении через сеть Интернет пакеты обрабатываются на интерфейсах маршрутизаторов со скоростью 170 пакетов/с. Если маршрутизатор имеет прямое подключение к сети Интернет, то он может как посылать пакеты в сеть Интернет, так и получать их из сети Интернет.  Рисунок 1. Схема сети Таблица № 14. Исходные данные для решения Задания 11
Таблица № 14. Исходные данные для решения Задания 11 (продолжение)
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
