Комплексные числа. Курсовая работа Комплексные числа. Решение задач по теме Комплексные числа в углубленном курсе алгебры и начал математического анализа
 Скачать 0.79 Mb. Скачать 0.79 Mb.
|
1.2. Геометрическая интерпретация комплексного числаДействительные числа геометрически изображаются точками координатной прямой. Мы выяснили, что комплексное число 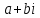 можно представить как пару действительных чисел можно представить как пару действительных чисел 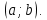 Поэтому естественно комплексные числа изображать точками плоскости. Поэтому естественно комплексные числа изображать точками плоскости.Пусть на плоскости задана прямоугольная система координат. Комплексное число 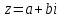 представляется на плоскости точкой с координатами представляется на плоскости точкой с координатами 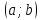 , и обозначается той же буквой , и обозначается той же буквой 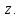 Такое соответствие между комплексными числами и точками плоскости взаимно однозначно: каждому комплексному числу 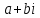 соответствует одна и только одна точка плоскости с координатами соответствует одна и только одна точка плоскости с координатами 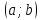 и, наоборот, каждой точке плоскости с координатами и, наоборот, каждой точке плоскости с координатами 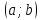 соответветствует одно комплексное число соответветствует одно комплексное число  Ось абсцисс называют действительной осью, а ось ординат называют мнимой осью. Начало координат – это точка 0. Плоскость, на которой изображаются комплексные числа, называют комплексной плоскостью. 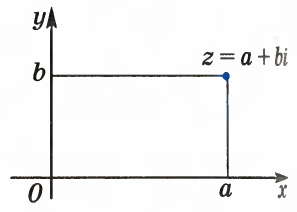 Рис. 1.2.1 Отметим, что точки 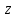 и и 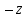 симметричны относительно точки 0 (начала координат), а точка симметричны относительно точки 0 (начала координат), а точка 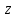 и и 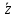 симметричны относительно действительной оси. симметричны относительно действительной оси.Комплексное число 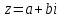 можно изображать вектором с началом в точке 0 и концом в точке можно изображать вектором с началом в точке 0 и концом в точке 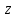 . Этот вектор будем обозначать той же буквой . Этот вектор будем обозначать той же буквой 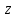 , длина этого вектора равна , длина этого вектора равна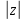 . .Число 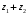 изображается вектором, построенным по правилу сложения векторов, а вектор изображается вектором, построенным по правилу сложения векторов, а вектор 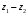 можно построить как сумму векторов можно построить как сумму векторов 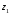 и и 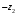 . .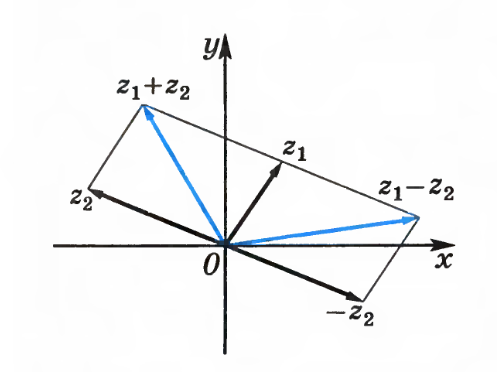 Рис. 1.2.2. Геометрический смысл модуля комплексного числа Пусть 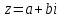 . Тогда по определению модуля . Тогда по определению модуля 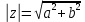 . Это означает, что . Это означает, что 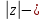 расстояние от точки 0 до точки расстояние от точки 0 до точки 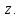 Например, равенство 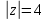 означает, что расстояние от точки 0 до точки означает, что расстояние от точки 0 до точки 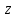 равно 4 (рис. 1.2.3). Поэтому множество всех точек равно 4 (рис. 1.2.3). Поэтому множество всех точек 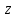 , удовлетворяющих равенству , удовлетворяющих равенству 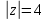 , является окружностью с центром в точке 0 радиуса 4. Уравнение , является окружностью с центром в точке 0 радиуса 4. Уравнение 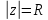 является уравнением окружности с центром в точке 0 радиуса является уравнением окружности с центром в точке 0 радиуса 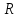 , где , где 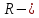 заданное положительное число. заданное положительное число.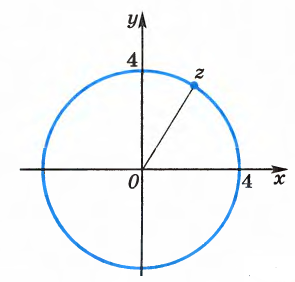 Рис. 1.2.3. Геометрический смысл модуля разности комплексных чисел. Выявим геометрический смысл модуля разности двух комплексных чисел, т.е. 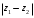 . Пусть . Пусть 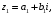 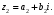 Тогда 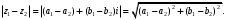 Нам уже известно, что это число равно расстоянию между точками с координатами Нам уже известно, что это число равно расстоянию между точками с координатами 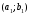 и и 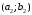 . .Итак, 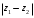 - расстояние между точками - расстояние между точками 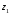 и и 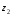 . . Например, расстояние между точками -1 и -3+3iравно 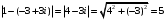 . .Так как 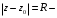 расстояние между точками расстояние между точками  и и 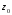 , то множество всех точек , то множество всех точек  , удовлетворяющих уравнению , удовлетворяющих уравнению 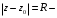 множество всех точек, расстояние от которых до точки множество всех точек, расстояние от которых до точки 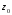 равно R. равно R. |
