Комплексные числа. Курсовая работа Комплексные числа. Решение задач по теме Комплексные числа в углубленном курсе алгебры и начал математического анализа
 Скачать 0.79 Mb. Скачать 0.79 Mb.
|
Комплексные числа1.1. Основные определения и действия с комплексными числамиКомплексным числом называют выражение вида 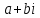 , где , где 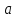 и и 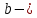 действительные числа, а действительные числа, а 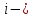 формальный символ (буква), для которого по определению выполняется равенство формальный символ (буква), для которого по определению выполняется равенство 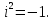 [] []Слово «комплексные» происходить от слова «составные» - по виду выражения 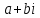 . Действительные числа . Действительные числа 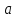 и и  , из которых составляется комплексное число , из которых составляется комплексное число 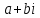 , называются компонентами этого числа. Число , называются компонентами этого числа. Число 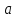 называется действительной частью комплексного числа называется действительной частью комплексного числа 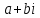 , вторая компонента , вторая компонента 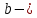 его мнимой частью. Число его мнимой частью. Число 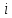 называют мнимой единицей. называют мнимой единицей.Например, действительная часть комплексного числа 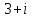 равна 3, мнимая часть равна 1. Запись комплексного числа в виде равна 3, мнимая часть равна 1. Запись комплексного числа в виде 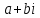 называют алгебраической формой комплексного числа. называют алгебраической формой комплексного числа.Два комплексных числа 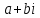 и и 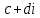 называются равными в том и только том случае, когда называются равными в том и только том случае, когда 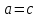 и и 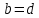 , т. е. когда равны их действительные и мнимые части. , т. е. когда равны их действительные и мнимые части.Например, 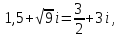 так как так как 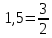 , , 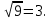 Сложение и умножение комплексных чисел. Операции сложения и умножения двух комплексных чисел определяются следующим образом. Сложение комплексных чисел 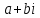 и и 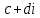 определяется правилом определяется правилом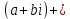 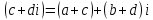 . (1.1.1) . (1.1.1)Умножение комплексных чисел 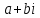 и и 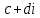 определяется правилом определяется правилом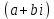 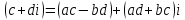 . (1.1.2) . (1.1.2)Формула (1.1.1) означает, что сложение производится по обычному правилу сложения многочленов с произведением подобных членов. Формула (1.1.2) означает, что умножение комплексных чисел осуществляется по обычному правилу умножения многочленов, только, считая, что 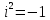 . .Принято считать, что 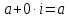 , т.е. комплексное число , т.е. комплексное число 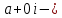 это действительное число это действительное число 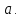 Число вида 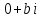 обозначают обозначают 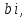 т.е. т.е. 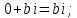 его называют чисто мнимым числом. его называют чисто мнимым числом.Комплексное число 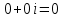 является единственным числом, которое одновременно и действительное, и чисто мнимое. является единственным числом, которое одновременно и действительное, и чисто мнимое.Комплексное число принято обозначать одной буквой, чаще всего буквой z. Запись 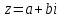 обозначает, что комплексное число обозначает, что комплексное число 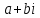 обозначается буквой обозначается буквой 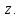 Операции сложения и умножения комплексных чисел обладают такими же свойствами, как и операции для действительных чисел. Основные свойства сложения и умножения комплексных чисел Переместительное свойство 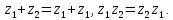 Сочетательное свойство 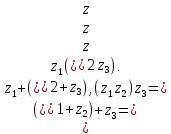 Распределительное свойство 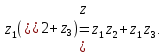 Сложения, умножение комплексных чисел фактически связаны с действительными числами-компонентами комплексного числа. Их можно изложить не используя символ 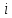 . Для этого достаточно писать вместо . Для этого достаточно писать вместо 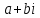 пару действительных чисел пару действительных чисел 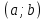 . .Комплексным числом zназывают пару 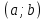 действительных чисел действительных чисел 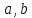 , взятых в определенном порядке. , взятых в определенном порядке.Тогда изложенные выше правила будут выглядеть следующим образом: 1. 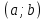 = =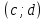 в том и только том случае, если в том и только том случае, если 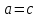 и и 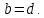 2. 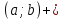 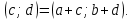 3. 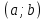 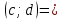 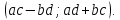 4. 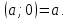 Число 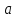 называют действительной частью комплексного числа и обозначают называют действительной частью комплексного числа и обозначают 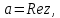 число число  называют мнимой частью комплексного числа и обозначают называют мнимой частью комплексного числа и обозначают 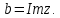 Комплексные числа 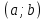 при при 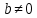 называют мнимыми числами, а числа вида называют мнимыми числами, а числа вида 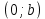 называют чисто мнимыми числами. называют чисто мнимыми числами.Комплексные числа 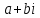 и и 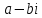 , отличающиеся знаком мнимой части, называются сопряженными. Если , отличающиеся знаком мнимой части, называются сопряженными. Если 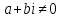 , то , то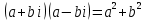 есть положительное действительное число. Обозначается сопряженное число 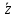 , т.е. , т.е.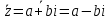 . .Например, 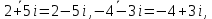 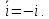 Отметим, что 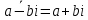 , поэтому для любого комплексного числа , поэтому для любого комплексного числа 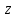 имеет место равенство имеет место равенство 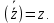 Равенство 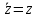 справедливо тогда и только тогда, когда справедливо тогда и только тогда, когда 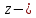 действительное число. действительное число.Модулем комплексного числа 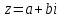 называется число называется число 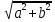 , т.е. , т.е.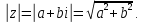 (1.1.3) (1.1.3)Например, 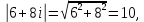 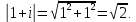 Из формулы (1.1.3) следует, что 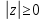 для любого комплексного числа для любого комплексного числа 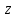 , причем , причем 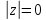 тогда и только тогда, когда тогда и только тогда, когда 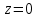 , т.е. когда , т.е. когда 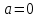 и и 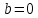 . .Для любого комплексного числа 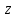 справедливы формулы справедливы формулы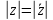 , , 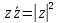 . .Вычитание комплексных чисел. Комплексное число 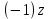 называется противоположным комплексному числу называется противоположным комплексному числу 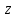 и обозначается и обозначается 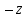 . .Если 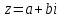 , то , то 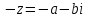 . Например, . Например, 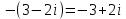 . .Для любого комплексного числа 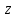 выполняется равенство выполняется равенство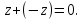 Вычитание комплексных чисел вводится как операция, обратная сложению: для любых комплексных чисел 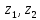 существует, и притом только одно, число существует, и притом только одно, число 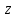 , такое что , такое что 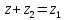 (1.1.4) (1.1.4)т.е. уравнение (1.1.4) имеет только один корень. Прибавим к обеим частям равенства (1.1.4) число 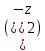 , противоположное числу , противоположное числу 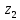 : :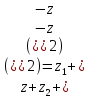 , откуда , откуда 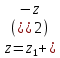 . .Число 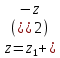 обычно обозначают обычно обозначают 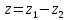 и называют разностью чисел и называют разностью чисел 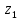 и и 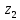 . .Если 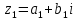 , , 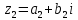 , то разность , то разность 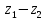 имеет следующий вид: имеет следующий вид: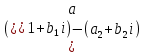 = =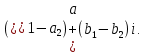 (1.1.5) (1.1.5)Формула (1.1.5) показывает. Что разность комплексных чисел можно находить по правилам действий с многочленами. Деление комплексных чисел. Деление комплексных чисел вводится как операция, обратная умножению: для любых комплексных чисел 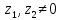 существует, и притом только одно, число существует, и притом только одно, число 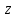 , такое, что , такое, что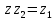 т.е. это уравнение относительно z имеет только один корень, который называется частным чисел т.е. это уравнение относительно z имеет только один корень, который называется частным чисел 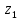 и и 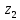 и обозначается и обозначается 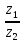 , или , или 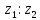 т.е. z= т.е. z=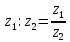 . .Комплексное число нельзя делить на нуль. Итак, частное комплексных чисел 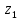 и и 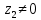 можно найти по формуле можно найти по формуле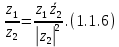 Каждое комплексное число z, не равное нулю, имеет обратное ему число w, такое, что z 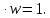 Если Если 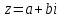 , ,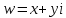 , то это равенство принимает вид , то это равенство принимает вид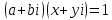 или или 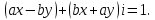 Из последнего равенства получаем систему 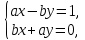 решая которую находим 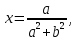 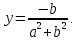 Таким образом, если 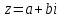 , то число, ему обратное, принимает вид , то число, ему обратное, принимает вид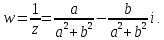 Если 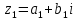 , , 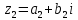 , то по формуле (1.1.6) можно представить в виде , то по формуле (1.1.6) можно представить в виде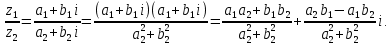 Вместо того чтобы запоминать эту формулу, следует запомнить, что результат для частного получается посредством умножения числителя и знаменателя на число сопряженное со знаменателем. Например, 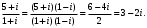 |
